平面向量积问题的解法策略探究

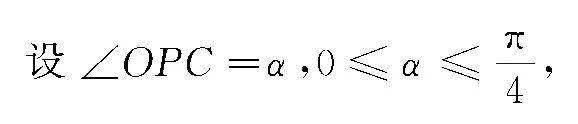
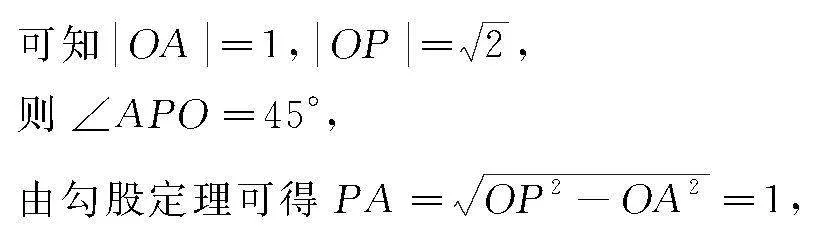
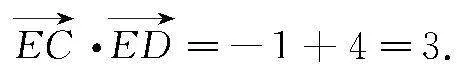
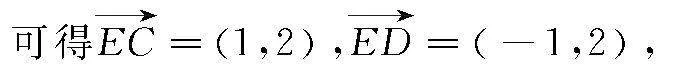
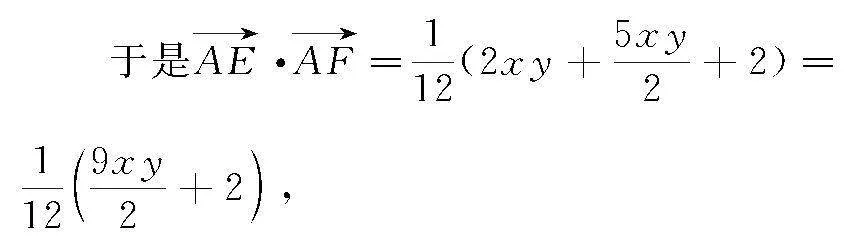
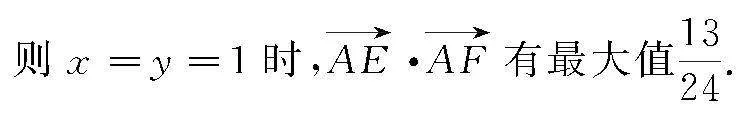
【摘要】平面向量积问题涉及的知识考点众多，与几何、函数、不等式联系紧密.解析转化时有多种思路，可从几何视角分析转化，也可借助三角函数知识求解，对于其中的最值与范围问题还可结合不等式的性质求解.本文结合考题，深入探究平面向量积问题的解法策略.

【关键词】向量积；高中数学；解题技巧

平面向量是高中数学的重点知识，其中的向量数量积问题在高考中出现的频次很高，常与平面几何、不等式、三角函数等知识相结合.解析该类问题时有三种策略：一是建立坐标系，利用向量积的坐标运算来求解；二是引入角作为变量，利用三角函数知识求解；三是代数运算，利用基本不等式求解.

1 构建坐标系解析

解 以A为坐标原点建立平面直角坐标系，如图1所示.

则E（1，0），C（2，2），D（0，2），

根据向量积的坐标运算可得：

评析 上述求解正方形背景下的向量积时采用了坐标系法，即建立平面直角坐标系，将向量坐标化，利用向量积的坐标运算直接求解.

2 三角函数解最值

分析 本题目以直线与圆相切为背景，求解向量积的最大值，可以引入角作为变量，利用三角函数知识来转化求解.

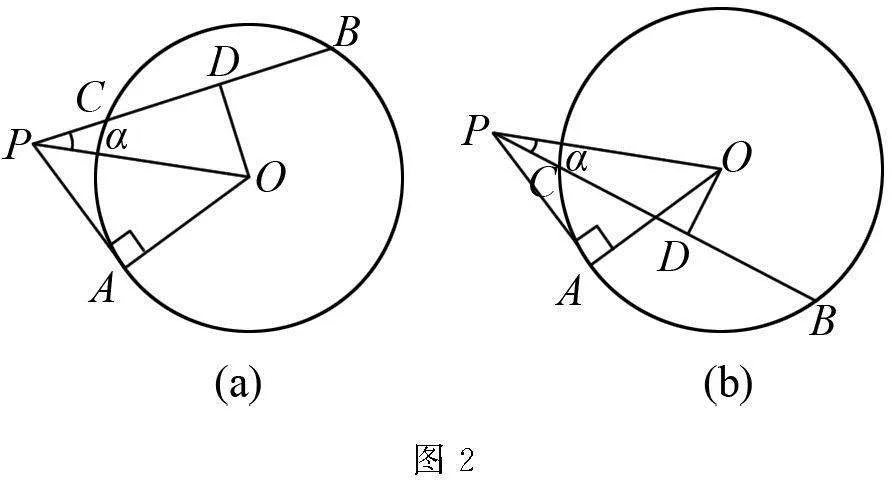
解 根据题意绘制图2所示图象，

分为如下两种情况讨论.

情形1 当点A，D位于直线PO异侧时，如图2（a）所示.

情形2 当点A，D位于直线PO同侧时，如图2（b）.

评析 上述解析直线与圆背景下的向量积最值时引入了角作为变量，转化为三角函数最值问题，进而利用三角函数的性质来求解最值.

3 基本不等式求最值

分析 第2空是关于三角形背景下的向量积最值问题，可先进行向量线性运算，再结合基本不等式的性质推导最大值.

在△ABC中，根据余弦定理：

BC2=x2+y2－2xycos60°=x2+y2－xy=1，

1129xy2+2，

结合x2+y2－xy=1和基本不等式x2+y2－xy=1≥2xy－xy=xy，可得xy≤1.

分析可知，当且仅当x=y=1取得等号.

评析 上述求解三角形背景下的向量积最值问题，采用了“向量线性运算+基本不等式”相结合的方法.设定参数，将向量积转化为代数式，再结合不等式的性质来求解.

4 结语

综上可知，求解平面向量积问题有三种转化解析策略，从几何视角分析，建立坐标系，利用坐标运算求解；从函数视角分析，利用三角函数性质解析；从不等式视角分析，利用不等式的性质求解，适用于最值与范围问题.探究学习中，需要理解向量积的几何意义，掌握向量运算与转化的方法，结合实例强化训练.