公式归纳，多维应用

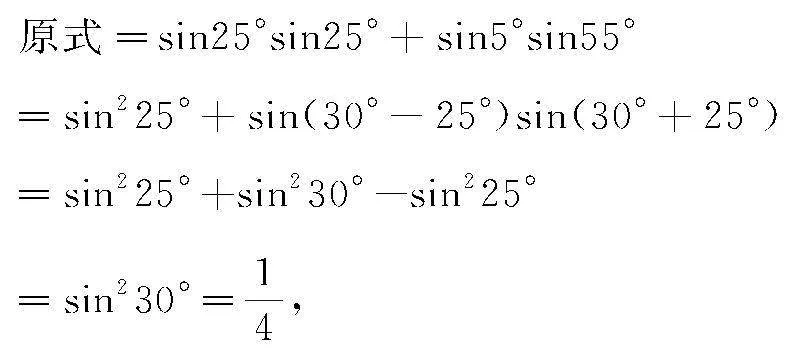
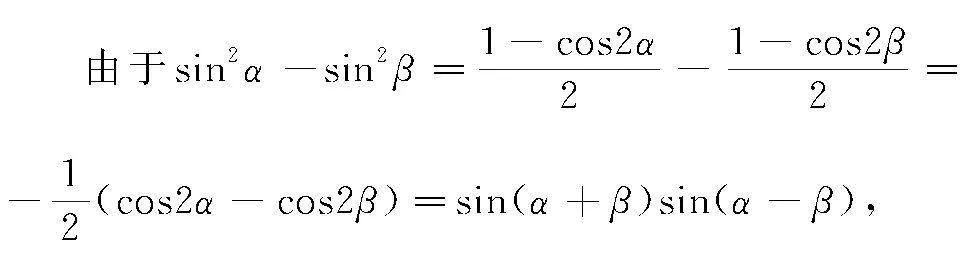
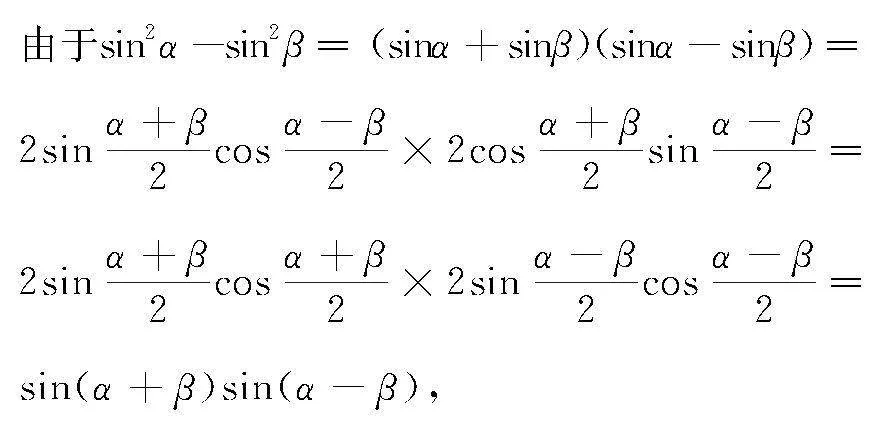
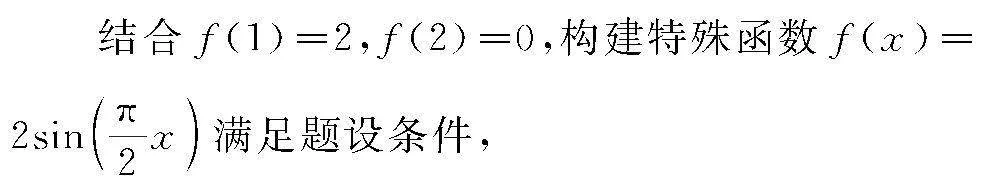
【摘要】三角函数中除了教材中的给出的一些基本公式，还有一些非常优秀的“二级结论”，在实际解题过程中有奇效．结合正弦平方差公式的展示、证明与拓展，并通过实例剖析该公式的多维应用，开拓数学思维，提升数学应用，引领并指导数学教学与复习备考．

【关键词】三角函数；正弦平方差；高中数学

正弦平方差公式是三角函数基本公式的深入与拓展，是三角函数及其应用中的一个重要公式，形式优美，当中涉及三角函数及其对应的代数运算，具有较为广泛的应用，是三角函数知识中的一个重要的“二级结论”，需要加以重视．

1 正弦平方差公式

1.1 公式

公式1 对于任意的实数α，β，都有sin2α－sin2β=sin（α+β）sin（α－β）成立．

1.2 公式证明

方法1 和差化积公式+二倍角公式法

故公式成立．

方法2 二倍角公式+和差化积公式法

由于sin2α－sin2β=1－cos2α2－1－cos2β2=－12（cos2α－cos2β）=sin（α+β）sin（α－β），

故公式成立．

方法3 两角和差公式法

故公式成立．

正弦平方差公式的形式直观，类似于代数中的平方差公式，是三角函数与代数知识的综合交汇与有机拓展，对于解决一些相关的应用问题有妙处．

1.3 公式拓展

公式2 （余弦平方差公式）对于任意的实数α，β，都有cos2α－sin2β=cos（α+β）cos（α－β）成立．

在公式1的正弦平方差公式的基础上，合理类比拓展即可得到以上余弦平方差公式．注意公式1与公式2之间的联系与区别．

2 正弦平方差公式的多维应用

2.1 三角求值问题

例1 计算：sin25°cos65°+sin5°sin55°=．

分析 根据题设条件，无法直接利用三角函数及三角恒等变换公式等加以求值，观察其中角的形式，借助诱导公式及角的加减运算加以变形，利用正弦平方差公式的转化与应用，从而实现非特殊角的三角函数关系式的求值与应用．

解 依题，借助正弦平方差公式，可得

点评 借助三角函数关系式中角的形式与代数关系，观察三角关系式的形式，综合利用三角函数及其三角恒等变换公式等加以应用，是解决此类问题的关键所在．而在具体解题时，抓住问题的根本，巧妙利用正弦平方差公式来转化，可以有效变形，实现问题的突破，得以有效求值．

2.2 解三角形问题

例2 在△ABC中，内角A，B，C的对边分别为a，b，c，若sin2B－sin2C=sinA，则B－C=．

分析 根据题设条件，综合正弦平方差公式、三角形内角和定理以及诱导公式等的应用，合理变形与转化，进而得以化简对应的三角关系式，得以确定对应的三角函数值，借助整体思维，得以确定相关角的代数式的大小．

解 依题sin2B－sin2C=sinA，

利用正弦平方差公式

sin2α－sin2β=sin（α+β）sin（α－β），

可得sin（B+C）sin（B－C）=sinA，

而sin（B+C）=sin（π－A）=sinA>0，

则有sin（B－C）=1，

而B－C∈－π，π，

点评 在实际解决一些相关的解三角形问题时，可以合理综合三角函数、三角形以及解三角形中的相关概念、公式与性质等，巧妙交汇，综合应用．这里借助正弦平方差公式进行合理变形，通过整体思维来分析并求解相关角的代数式的值．

2.3 抽象函数问题

例3 （2023届江苏省南京市高三（上）学情调研数学试卷（9月份））已知函数f（x），任意x，y∈R，满足f2（x）－f2（y）=f（x+y）f（x－y），且f（1）=2，f（2）=0，则f（1）+f（2）+…+f（90）=（ ）

（A）－2. （B）0. （C）2. （D）4.

分析 根据题设条件，挖掘抽象函数的结构特征，吻合正弦平方差公式，合理联想并创新构建三角函数模型，并利用特殊函数值加以配凑对应函数的系数，借助特殊值法加以转化与应用，综合函数的基本性质加以分析与求解．

解 依题f2（x）－f2（y）=f（x+y）f（x－y），吻合正弦平方差公式sin2x－sin2y=sin（x+y）sin（x－y），

则知该函数f（x）是以4为周期的函数，也是一个奇函数，有f（0）=0，

依f（1）=2，f（2）=0，可得f（3）=f（－1）=－f（1）=－2，f（4）=f（0）=0，

则f（1）+f（2）+f（3）+f（4）=0，

所以f（1）+f（2）+…+f（90）=22×f（1）+f（2）+f（3）+f（4）×22+f（1）+f（2）=2.

故选择答案：（C）．

点评 借助抽象函数的结构特征与对应的公式形式构建联系，通过特殊值法的应用来构建特殊函数模型，是解决一些相关问题中比较常见的一种思维方法．熟练掌握一些具有特定结构特征的基本初等函数类型，为解决此类问题的特殊函数模型思维提供理论依据，也是综合创新应用的基础．