帮你走出数列的两大“雷区”

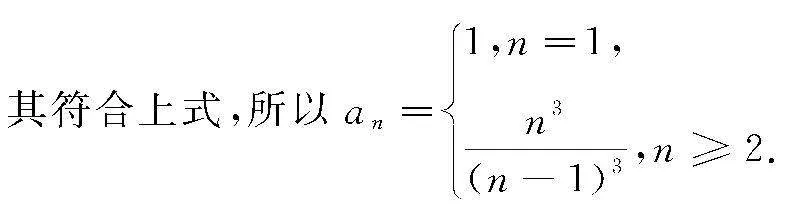
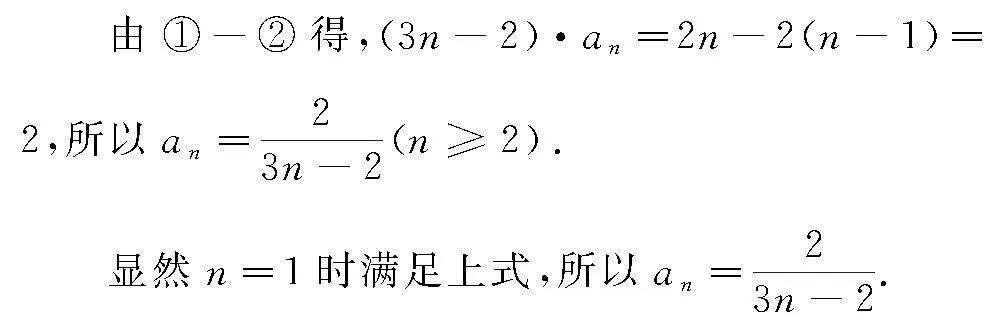
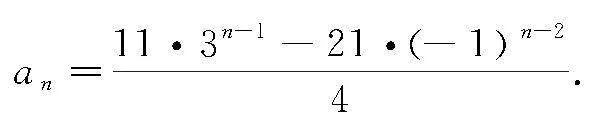
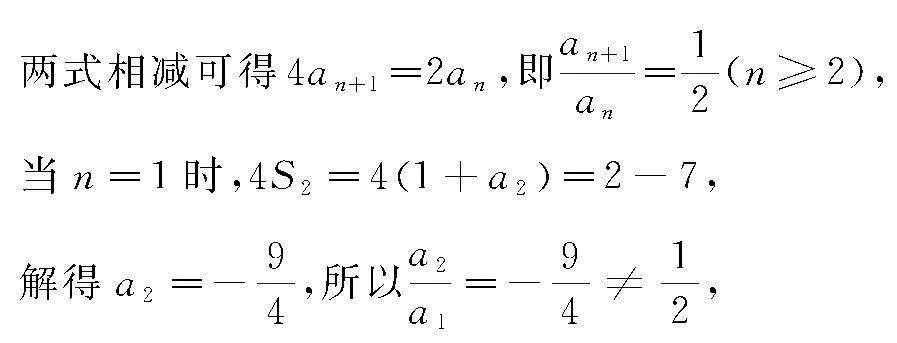
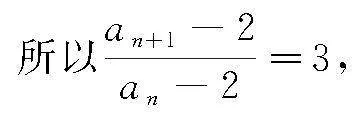
【摘要】数列模块在高考中占有非常重要的位置，近几年的高考试题中，数列部分一般是一个大题、一个小题，占20分左右，难度中等，但由于数列中知识点较多、关系复杂，历届考生经常在数列问题上因思维不严谨、方法不灵活而出错.为此，梳理数列中易出错的两大“雷区”，以期引起学生的警示，帮助学生成功地走出“雷区”，从而加深对数列的理解，培养学生思维的灵活性和严谨性.

【关键词】数列；函数；高中数学

雷区1 忽视n=1是否需要验证的问题

教学中发现不少学生总是搞不清楚到底是否需要验证n=1，非常困惑与苦恼，这类问题主要有以下两种类型.

类型1 已知前n项和Sn求an时，是否需要验证n=1.

该类型必须验证n=1，这是因为an=Sn－Sn－1这个关系式只适合于n≥2，n=1时无意义.

例1 在数列an中，前n项和Sn=3n2－4n，那么数列an的通项公式an= .

解 a1=S1=3－4=－1，

当n≥2时，an=Sn－Sn－1=3n2－4n－3（n－1）2－4（n－1）=6n－7，

又因为a1适合上式，

所以an=6n－7.

变式1 若将上题中的Sn=3n2－4n改为Sn=3n2－4n+1，那么数列an的通项公式an＝.

解 a1=S1=3－4+1=0，

当n≥2时，an=Sn－Sn－1=3n2－4n－3（n－1）2－4（n－1）=6n－7，又因为a1不适合

点评 上述步骤可以简称为“三步走”，三个步骤缺一不可，尤其是第三步验证n=1，恰是学生容易遗漏的步骤.在验证n=1之后，结果有两种情况：如果a1适合第二步的式子，最后结果就用第二步的一个式子进行表示；如果a1不适合第二步的式子就要写成分段的形式.因此，这种题型必须验证n=1.

例2 已知数列an满足a1+4a2+…+3n－2an=2n，则an＝.

解 当n=1时，a1=2，

因为a1+4a2+…+3n－2an=2n①，

所以a1+4a2+…+3n－5an－1=2n－1，n≥2②，

变式2 已知数列an的首项a1=1，且满足a1·a2·a3·…·an=n3n≥2，则an= .

解 因为a1·a2·a3·…·an=n3n≥2，

a1·a2·a3·…·an－1=n－13n≥3，

又因为a1=1，a1·a2=23，所以a2=23，

点评 例2虽然不是以Sn的形式出现的，但等式a1+4a2+…+3n－2an=2n左边也是和的形式，因此实质上和例1是同一种题型；变式2是已知前n项积Tn求an，和已知前n 项和Sn求an的道理一样，即必须验证n=1.

类型2 等差（等比）数列的判定时是否需要验证n=1.

例3 已知Sn表示数列an的前n项和，首项a1=1，且4Sn+1=2Sn－7n∈N*．求数列an的通项公式.

解 因为4Sn+1=2Sn－7，

所以当n≥2时，4Sn=2Sn－1－7，

所以数列an从第二项起是等比数列，

雷区2 构造新数列之后，混淆新旧数列的关键项

构造新数列之后，新数列的首项、第n项等关键项与旧数列是不同的，一定要搞清新、旧数列的关键项，才能成功地避开雷区.

例4 已知数列an的首项a1=4，an+1=3an－4，求数列an的通项公式.

解 设an+1+x=3an+x，

即an+1=3an+2x，

又an+1=3an－4，

所以x=－2，

故an+1－2=3an－2.

又因为a1－2=2，

所以an－2是等比数列，首项为2，公比为3，

所以an－2=2×3n－1，

所以an=2×3n－1+2.

点评 构造新数列an－2之后，新数列的首项是a1－2，而不是a1.

变式3 已知数列an中，a1=8，a2=3，an=2an－1+3an－2n≥3，求这个数列的通项公式.

解 因为an=2an－1+3an－2，

所以an+an－1=3an－1+an－2，

又a1+a2=11，

所以an+an－1是首项为11，公比为3的等比数列，

则an+an－1=11×3n－2①，

又an－3an－1=－an－1－3an－2，a2－3a1=－21，

所以an－3an－1是首项为－21，公比为－1的等比数列，则an－3an－1=－21·－1n－2②，

①②两式组成方程组即可解得

点评 ①②两式中等号右边3的指数是n－2，而不是n－1，这是因为an+an－1是数列an+an－1的第n－1项，而不是第n项.