基于CGDNN的低信噪比自动调制识别方法

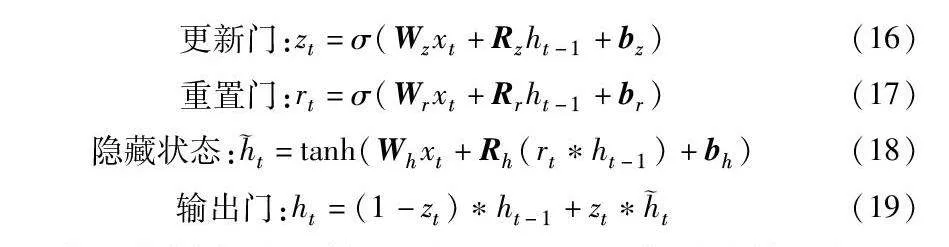
摘 要：针对非协作通信环境中，自动调制识别（automatic modulation recognition，AMR）在低信噪比下泛化能力有限、分类精度不高的问题，提出一种由卷积神经网络、门控循环单元和深度神经网络组成的模型—CGDNN（convolutional gated recurrent units deep neural networks）。首先对I/Q采样信号进行小波阈值去噪，降低噪声对信号调制识别的影响；然后用CNN和GRU提取信号空间和时间特征；最后，通过全连接层进行识别分类。与其他模型对比，验证CGDNN模型在提高AMR性能的同时，显著降低了计算复杂度。实验结果显示，CGDNN模型在RML2016.10b数据集上的平均识别准确率达到了64.32%，提高了-12 dB～0 dB的信号分类精度，该模型大幅减少了16QAM与64QAM的混淆程度，在18 dB时达到了93.9%的最高识别准确率。CGDNN模型既提高了低信噪比下AMR的识别准确率，也提高了模型训练的效率。

关键词：自动调制识别； 小波阈值去噪； 卷积神经网络； 门控循环单元； 深度神经网络

中图分类号：TN92 文献标志码：A

文章编号：1001-3695（2024）08-034-2489-07

doi：10.19734/j.issn.1001-3695.2023.11.0581

Low signal-to-noise ratio automatic modulationrecognition method based on CGDNN

Zhou Shunyonga，b， Lu Huana，b， Hu Qina，b， Peng Ziyanga，b， Zhang Hanglinga，b

（a.School of Automation & Information Engineering， b.Artificial Intelligence Key Laboratory of Sichuan Province， Sichuan University of Science &; Engineering， Yibin Sichuan 644000， China）

Abstract：To overcome AMR’s limited generalization and low classification accuracy in non-cooperative communication contexts with low signal-to-noise ratio， this paper proposed a model named CGDNN，which integrated CNN， GRU and deep neural networks. To mitigate noise impact on modulation detection， this paper initially denoised I/Q sampled signal using wavelet thresholding. Subsequently， this paper utilized CNN and GRU for extracting spatial and temporal features from signals before proceeding to classification through fully connected layers. Besides enhancing AMR performance， the CGDNN model significantly reduced computational complexity compared to competitors. Experiment results demonstrate an average recognition accuracy of 64.32% on the RML2016.10b dataset， with an enhancement in signal classification accuracy from -12 dB to 0 dB. Moreover， the model substantially decreased confusion between 16QAM and 64QAM， achieving a peak recognition accuracy of 93.9% at 18 dB. CGDNN model effectively improved AMR detection accuracy under low signal-to-noise ratio conditions and enhanced model training efficiency.

Key words：automatic modulation recognition; wavelet threshold denoising; convolutional neural networks; gated recurrent unit; deep neural network

0 引言

自动调制识别通过对发射信号源采用的通信技术和调制方案进行识别分类，以此分析检测到的无线电信号并获取相关有效信息。因此，自动调制识别使得接收机在非合作通信场景下自动识别信号调制方案成为可能，并广泛应用于军事和民用领域，例如无线电频谱检测［1］、认知无线电［2］和自适应调制器。它作为信号检测和解调之间的桥梁，能够对接收信号调制类型进行调制模式识别。

传统的机器调制识别的方法分为基于似然（likelihood-based，LB）的方法和基于特征（feature-based，FB）的方法［3］。LB方法通过评估接收信号的似然函数并将似然比与预定义的阈值比较来作出决策，最大限度地减少了错误分类的概率，但其计算复杂度很高［3］；FB方法通过仔细选择手工制作的特征，利用机器学习算法进行分类，可以实现接近最佳的性能。这种方法可以在特定任务中取得高精度，但在一般情况下可能面临挑战，因为手动设计的特征无法全面反映各种现实世界通信信道的影响。

较早的信号调制模式识别主要采用人工识别的方法，利用相关仪器人工观察和判断信号的时频域特性。但这种方法依赖于研究人员的专业知识水平和识别经验，无法保证调制识别的准确度。尤其是在信噪比较低的情况下，存在信号与噪声难以区分、多路径干扰等原因，使信号的质量下降，接收端的信号变得模糊，难以正确解调和识别。

目前，深度学习（deep learning，DL）在自然语言处理、计算机视觉和机器人［4］等各应用领域取得了巨大的成功。与传统方法相比，应用在AMR方法的DL在识别精度和复杂性方面表现出了更高的性能。O’Shea等人［5］首次将DL应用在AMR中，提出卷积神经网络（convolutional neural network，CNN），显示出了CNN对复值时间无线电信号域的适应及改进性能，证明了CNN在低信噪比下对大型且密集编码的时间序列进行盲时间学习是可行的。Daldal等人［6］提出将深度长短期记忆网络（long short-term memory network，LSTM）模型应用于数字调制信号。West等人［7］应用卷积长期短期深度神经网络（CLDNN），十分有效地提高了识别精度。Huang等人［8］通过门控循环单元（gated recurrent unit，GRU）获取信号时间信息并扩展信号特征维度，以得到满意的分类性能。

近年来，DL在AMR领域取得了重大进展。在高信噪比下，现有的AMR模型获取了高识别精度，在AMR模型之前应用信号去噪算法是提高AMR性能的方法之一［9］，但信道环境的复杂性和多种噪声特性使得AMR在低信噪比下分类精度很难提高，导致了低信噪比下的调制识别充满挑战。因此，本文提出了一种结合小波变换和DL的CNN、GRU及DNN（deep neural network）组成AMR模型，来通过基于小波变换的自适应阈值实现对输入信号的去噪，再使用CGDNN对调制信号进行识别，显著提高低信噪比下的识别准确性。

1 信号模型与小波去噪

1.1 信号模型

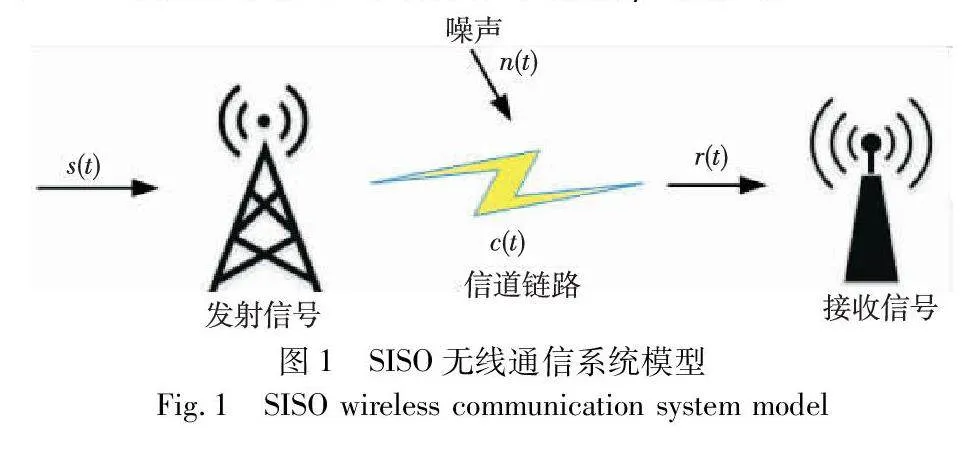
无线通信系统一般包括发射机、信道和接收机，如图1所示。本文考虑的是单输入单输出通信系统（SISO），接收信号r（t）表示为

r（t）=s（t）c（t）+n（t）（1）

其中：s（t）表示发射信号；表示卷积运算；c（t）是发射无线信道的时变脉冲响应，如式（2）所示；n（t）表示信道干扰，指均值为零的加性高斯白噪声（AWGN）。

c（t）=aδ（t-τ）（2）

其中：a是信号幅度；δ表示脉冲函数；t是时间间隔；τ表示信道多径延迟。

模数转换器以fs=1/Ts的速率对接收信号r（t）进行n次采样，生成离散时间观测信号r（n）。离散信号r（n）分解为同相分量rI（n）和正交分量rQ（n），信号表示为

r（n）=rI（n）+j×rQ（n）（3）

其中：j表示虚数单位，即j2=-1。

式（4）描述了现实世界中真实环境的各种因素，表示为

r（t）=ejnLo（t）∫τ0τ=0（s（nClk（t-τ））h（τ）+nAdd（t））dt（4）

其中：nLo是残余载波随机游走过程；nClk是随机游走重采样;h（t-τ）表示时间相关的非恒定信道脉冲响应；nAdd（t）是可能添加的噪声，包括AWGN或其他噪声［5］。

接收信号r（t）在AMR中通常处理为IQ分量来表达信号，IQ分量表示为

I=A cos φQ=A sin φ（5）

其中：A表示接收信号r（t）是瞬时幅度;φ是相位。

自动调制识别对接受到的无线通信信号的调制方式进行分类，本质上是一个多分类任务［10］。调制分类主要是识别接收信号的特征信息并确定其调制类型。调制识别算法一般是根据设定模型的速度和识别准确性来评估的。现有的AMR方法一般是在高信噪比的条件下实现高精度，但这与现实环境不符。在低信号电平下，基于深度学习的AMR会因为各种背景噪声而大大增加对调制分类的难度，例如频率选择性衰落、本地振荡器偏移、多普勒偏移、加性高斯白噪声、脉冲噪声、同信道干扰等。因此，对低信噪比下的调制识别分类是一项具有挑战性的任务。本文为了提升低信噪比下的准确性，使其更加接近现实环境，在原始信号中加入小波域去噪，从而降低噪声对调制分类的影响。

1.2 小波去噪

Donoho［11］提出小波阈值去噪算法，通过选定的阈值函数修改信号的小波分解系数来消除信号噪声。原始信号经过小波分解，能量分布在少数小波系数上，这些小波系数显著地分布在各个分解尺度上［12］。然后对小波变换后的小波系数进行变换，选择软阈值去噪算法，通过自适应地选择阈值函数对信号进行去噪。最后对处理后的小波系数进行小波逆变换，重新合成去噪后的信号。算法流程如图2所示。

考虑一个信号xi，含高斯随机噪声zi～N（0，σ2），其噪声信号表示为

yi=xi+zi i=0，1，…，N-1（6）

在噪声信号yi中，找到原始信号xi的近似值i，从而最小化均方误差。

‖x-‖1N∑N-1i=0xi-i2（7）

其中：x=［x0…xN-1］T及=［0…N-1］T。令W表示正交小波变换，式（6）可以写成

dj=cj+εj（8）

那么d=Wy，c=Wx及ε=Wz。基于小波阈值去噪的过程表示为

u=Wy=D（u，λ）=W-1（）（9）

小波变换可以通过多尺度变换在时域和频域上显示信号的特征，连续小波变换W方程表示为

WT（a，τ）=1a∫∞-∞f（t）·ψ（t-τa）dt（10）

其中：a为尺度参数，控制小波函数的缩放;τ为平移参数，反映了某一时刻的信号信息；f（t）为原始信号。

离散小波变换是将连续小波变换离散化，从而找到相互正交的基函数，通过离散小波变换，将原始信号分解为低频分量和高频分量两个部分。通过低通滤波器的信号系数称为近似分量，而高通滤波器的系数称为细节分量。近似分量包含原始信号的大部分能量，对细节分量进行阈值处理可以减少信号中的噪声，通过逐层分解，以获取不同尺度上的信号。因子a对信号进行采样，对应相应尺度变化。离散小波变换方程表示为

f（x）=1N［Tφ（0，0）φ0，0（x）+∑J-1j=0∑2j-1k=0Tψ（j，k）ψj，k（x）］（11）

其中：Tφ（0，0）和Tψ（j，k）分别表示近似系数和细节系数，表示为

Tφ（0，0）=〈f（x），φ0，0（x）〉=1N∑N-1x=0f（x）φ（x）（12）

Tψ （j，k）=〈f（x），ψj，k （x）〉=1N∑N-1x=0f（x）ψ*j，k （x）（13）

通过小波变换得到含噪信号y的小波系数u，考虑到多贝西小波（Daubechies wavelet）主要应用在离散型的小波转换，其不但可以去除信号噪声，并且该小波作为稀疏基引入的光滑误差不易被察觉，使得小波重构过程中得到的信号比较光滑。因此小波基函数选择“Db6”，即小波阶数为6的紧支集正交小波，然后通过正交小波进行非线性去噪运算得到去噪后的小波系数，λ表示阈值，根据自适应的阈值应用于小波系数上，再将其传递给阈值函数。最后进行小波逆变换W-1获得估计值。

选择合适的阈值函数和阈值大小是小波阈值去噪的关键问题。小波阈值函数最常见的是硬阈值函数和软阈值函数。硬阈值通过比较小波系数的绝对值与一个给定的阈值，将小于阈值的系数置零，而将大于阈值的系数保持不变，但这意味着硬阈值去噪完全消除了那些被认为是噪声的小波系数，而保留了那些被认为是信号的系数，这可能会导致信号在去噪后出现较多失真，从而丢失一些信息；软阈值函数在硬阈值的基础上引入平滑过渡，对于小于阈值的系数，软阈值去噪将其减小到零，并对大于阈值的系数进行缩放，这样可以更好地保留信号的主要特征并减少失真，得到整体连续性较好的小波系数［13］。因此，本文选择软阈值函数进行去噪，其表达式为

uλ=［sign（u）］（u-λ） u≥λ

0 u<λ（14）

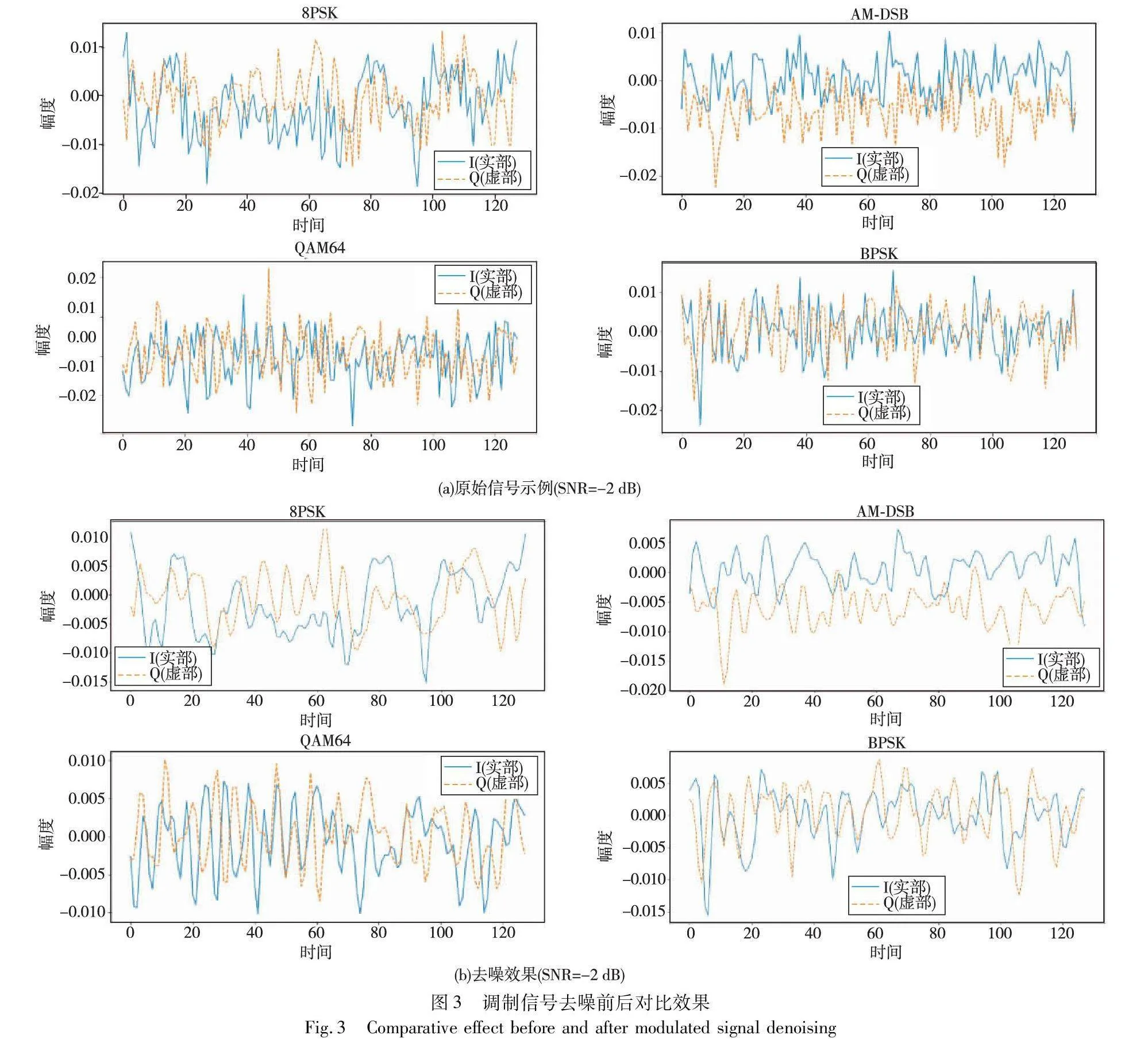
其中：sign为符号函数；u是小波系数的值；uλ是小波系数设定的阈值。实验采用自适应阈值的方法，其工作机制是根据不同信噪比调整阈值大小，并通过不同的噪声效应来选择阈值。当信号相对较强时，选择的阈值较小，以保留更多细节；当信号较弱时，阈值选择较大，以减小噪声的影响。将设定的小波阈值去噪算法运用在各种调制信号上以消除其噪声的影响，图3展示了不同调制信号在信噪比为-2 dB条件下原始信号示例与去噪之后的效果。

2 AMR模型

本文提出了一种基于DL的AMR网络模型—CGDNN，由卷积神经网络、门控循环单元及全连接深度神经网络组成。首先通过flatten层和dense层组成的神经网络对I/Q样本进行参数估计得到相位参数，并利用lambda层和multiply层对参数进行变换得到输出。然后将变换后的参数数据作为CGDNN的输入，具有64个滤波器的CNN对信号I/Q序列进行空间特征提取，128个单元的GRU对信号I/Q序列进行时间特征提取，最后分类由dense层完成，其隐藏神经元数量与调制方式数量一致。CGDNN结构框架如图4所示。

2.1 参数估计与变换

在前面信号模型中所提到的采样I/Q样本受各种通道噪声干扰，以及不完善的硬件条件的影响，这些都可能会导致接收信号的时间移位、线性混合和旋转［14］。为了降低这些不利因素的影响，在文献［14］的启发下，通过对I/Q信号数据进行参数估计和参数变换以提取相位偏移信息，并对相位参数进行变换，调整信号的特征使问题变得更简单。在选择性地去除或减弱不必要部分的同时突出信号特征，使其更容易分析，以此提高调制识别准确率。

flatten层对输入信号尺寸为2×128的I/Q样本展平为一维张量，来满足dense层的输入维度，dense层对张量中的数据进行相关线性变换以得到相位参数。通过自定义层进行参数变换，应用lambda层对得到的相位参数调用函数计算其余弦值和正弦值，multiply层对输入信号和之前所得的余弦和正弦进行逐元素相乘，再利用add层和subtract层对相乘的结果进行逐元素相加和相减，将所得结果连接并打印为张量作为CGDNN结构的输入。

2.2 卷积神经网络

CNN作为一种前馈神经网络，由多层神经网络组成，其神经元可以响应周围单元的部分覆盖，在局部特征提取方面具有明显的优势。CNN主要由卷积层和池化层等结构组成。卷积层作为CNN的基本组成，使用卷积滤波器从输入数据中提取信号空间特征，其目的是学习特征并与可学习内核进行卷积，卷积运算可以表示为

X（i，j）=∑m∑nx（m+i，n+i）ω（m，n）+b（15）

其中：X（i，j）表示卷积输出；x是输入矩阵；ω是大小为m×n的权重矩阵；b为偏置。

在实验中提出的CGDNN模型，一共包含两个卷积模块，即Conv2D（64）和Conv2D（15）。第一个卷积模块对应组成为64个2×8卷积核，以提取信息的空间特征，且使用零填充，使输入和输出的特征图大小相同。第二个卷积模块由15个1×5的卷积核构成，以进一步压缩提取的特征，同样使用零填充，保持其特征图高度不变，对其卷积层的输出进行批量归一化处理。两个卷积模块都使用了修正线性单元激活函数ReLU，通过引入非线性变换，增强网络的表达能力。批量归一化层（batch normalization，BN）对每个批次的特征进行归一化处理，减少了内部协变量偏移，在训练期间不断改变特征分布，提高了网络模型的泛化能力。在第一个卷积模块中加入的最大池化层减小了特征图的空间大小，将每个区域中最显著特征提取出来，同时减少了模型参数数量。

2.3 门控循环单元

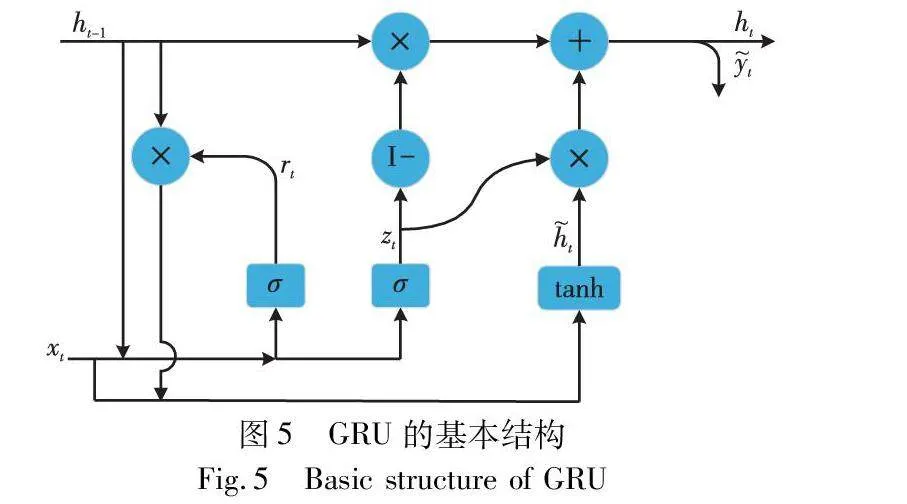
GRU是循环神经网络中一种改进结构，通过引入“门”机制和记忆单元，检测调制信号序列内的时间变化，具有学习长期依赖关系的能力。其基本结构如图5所示。

图中各种分量的计算式表示为

更新门：zt=σ（Wzxt+Rzht-1+bz）（16）

重置门：rt=σ（Wrxt+Rrht-1+br）（17）

隐藏状态：t=tanh（Whxt+Rh（rtht-1）+bh）（18）

输出门：ht=（1-zt）ht－1+ztt（19）

其中：σ表示信号激活函数；矩阵W、R和b分别是输入权重、循环权重和每个分量的偏差的集合。其中更新门可以更新信息和隐藏层的状态，在保证网络精度的同时减少了网络参数。

实验设计的GRU层提取128个单元的信号时间特征，GRU作为序列模型循环神经网络的一种变体，能够有效地提取序列数据的时间相关性特征，具有抵抗梯度爆炸和消失的优点。在模型中，对GRU层的输出进行批量归一化后提高模型稳定性，再利用全局平均池化层将时间序列维度降至1，通过减少特征图的维度，从而减少了模型的参数数量，降低了计算成本。同时应用了非线性激活函数—高斯误差线性单元GELU，允许网络学习复杂的非线性关系。

2.4 全连接层

CGDNN模型的分类层由dense层和softmax组成，通过dense层完成调制信号的分类识别，其激活函数设置为softmax，将输出转换为类别的概率分布。dense层实际是一个卷积层，主要利用卷积核和偏置的初始化以提高网络的性能和收敛效果，对其进行正则化处理防止过拟合，从而更好地适应训练数据。其中使用偏置的作用是增加模型的灵活性，同时也增加dense层每个神经元的可学习参数数量，以提高模型的表达能力。

算法1为基于深度学习的AMR算法的伪代码实现过程。其输入为张量形状大小2×128的信号I/Q样本，输出为调制识别的分类结果。首先对输入数据进行参数估计与参数变换来突出信号特征，同时，定义了两个卷积模块和GRU网络层，分别用以提取信号的空间特征和时间特征，最后通过dense层完成调制分类。

算法1 基于深度学习AMR算法

输入：主输入张量形状大小为2×128，附加输入张量形状大小为1×128。

输出：分类结果。

# 输入参数估计

x1=Flatten（） //I/Q信号样本展平为一维张量

x1=Dense（activation="linear"） //进行线性变换得到相位参数

# 参数变换

cos1=Lambda（cos）（x1）

sin1=Lambda（sin）（x1） //计算余弦和正弦值

x11=逐元素乘法操作（input1， cos1）

x12=逐元素乘法操作（input2， sin1）

x21=逐元素乘法操作（input2， cos1）

x22=逐元素乘法操作（input1， sin1） /*分别对两个维度应用余弦和正弦变换*/

y1=Add（x11， x12）

y2=Subtract（x21， x22）

x33=Concatenate（y1， y2） //拼接

define block1： //提取空间特征

XCV=Conv2D（x）

XBN=BatchNorm（XCV）

Xmax=MaxPool2D（XBN）

end define

define block2： //提取空间特征

XCV=Conv2D（Xmax）

XBN=BatchNorm（XCV）

return XBN

end define

define GRU： //提取时间特征

XGRU=CuDNNGRU（x）

XBN=BatchNorm（XGRU）

XGELU=GELU（XBN）

return XGELU

end define

begin：

step1：

输入参数估计

step2：

x3=Block1（x33）

x3=Block2（x3）

step3：

x4=GRU（x3）

step4：

x5=Dense（x4）

return x5 //输出分类结果

end

2.5 激活函数

激活函数能够提高网络的非线性能力，表1提供了网络模型中所用的激活函数，如线性单元ReLU、高斯误差线性单元GELU和softmax。在CNN结构中使用了整流线性激活函数ReLU，以加快收敛速度。该激活函数能解决网络中梯度消失的问题，从而极大地提高网络的正确性。该函数是一个分段线性函数，只保留正数部分，其具有一个理想特性，即在经过ReLU激活后表现为稀疏状态，其优越性能就来源于这种稀疏性［15］。ReLU函数产生的负值会被稀疏，并且这种稀疏性呈动态变化趋势。在进行梯度训练时，网络会通过自动调节稀疏比率，以确保激活数据中存在合理数量的非零值。这样的处理将复杂特征转换为稀疏特征，从而使这一部分特征更具有鲁棒性。

GELU作为一种基于高斯误差函数的激活函数，相较于激活函数ReLU更加平滑，在梯度传播中也更加稳定，因此更容易收敛于训练过程。其引入的非线性变换使得网络能学习更复杂的映射，从而能够更好地提高训练性能。GELU通过非线性输入进行加权，而ReLU对输入进行门控［16］。这里的两种激活函数都很少出现梯度消失的现象，因此，能更好地支持深层神经网络的训练和优化。softmax激活函数将上一层的数据进行归一化，对其进行多分类的目标预测，使得模型在训练过程中学习适当的权重。

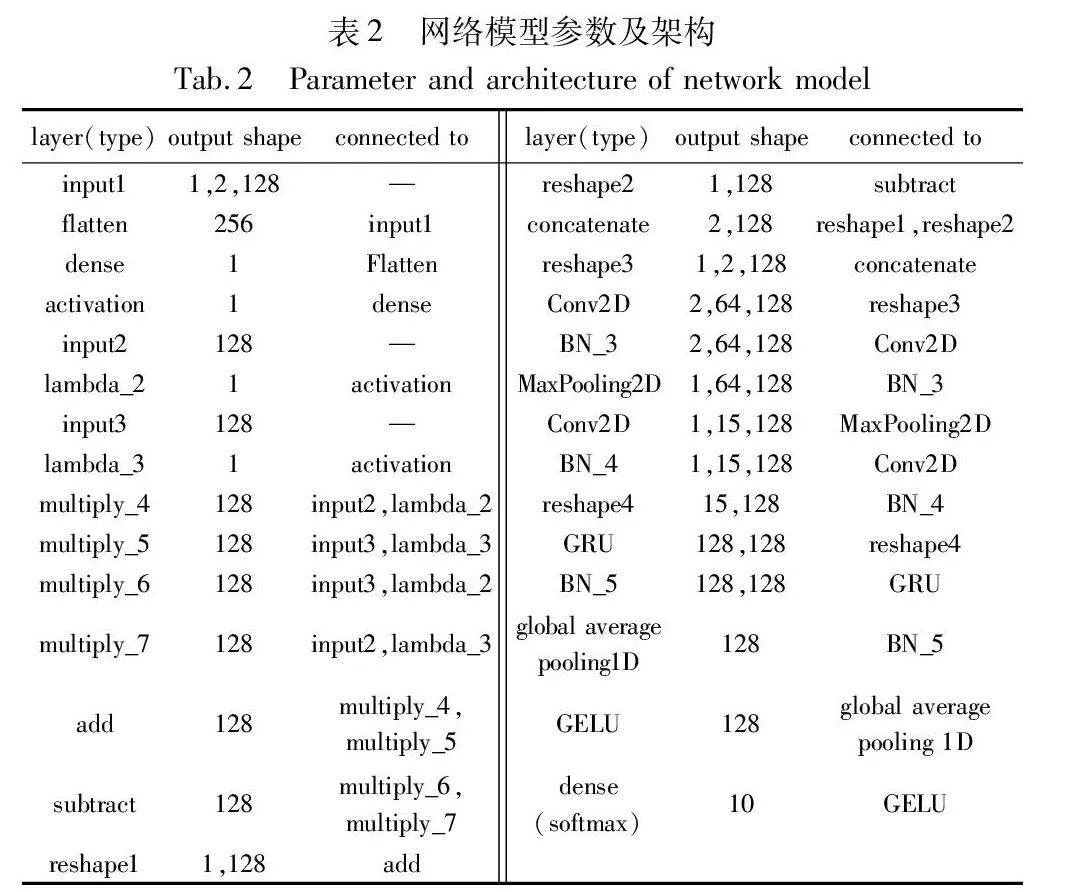
2.6 模型复杂度

通过计算神经网络训练中的参数总数来衡量模型复杂度。模型总参数量为63 958，模型参数会影响模型的内存使用情况，也决定了模型的大小。表2提供了构建网络模型的参数和详细结构。

对于模型的复杂度，需要平衡滤波器数量和网络深度以达到最佳性能。在保持网络训练结果的同时，通过增加网络的宽度和深度，可以有效提高网络质量。网络模型的计算量可以通过调整卷积层中的卷积核数量和大小来降低。特别是在模型计算方面，较大空间滤波器的卷积往往会导致昂贵的计算成本。

在具体实现中，第一个卷积层采用64个大小为2×8的卷积核，虽然选择的卷积核相对较大，但通过更多的参数，使得模型能够学习到更多更复杂的特征。而第二个卷积层的卷积核大小为1×5，参数减少到原来的5/16，同时也压缩了卷积核数量，这种设计在进一步提取特征的同时减小了特征图数量，从而有效降低了模型的计算量，提高了网络训练的高效性。这种平衡和调整确保模型在性能和计算效率之间取得最佳平衡。

3 实验与讨论

3.1 实验数据集

仿真实验在RML2016.10b［17］数据集上进行，其数据输入维度为2×128。它包含1 200 000个信号，具有十种调制类型方式，包括八种数字信号BPSK、QPSK、8PSK、16-QAM、64-QAM、CPFSK、GFSK、4PAM和两种模拟信号WBFM、AM-DSB，每个数据样本由128个采样IQ样本点组成，其中每个复杂时间样本的实部和虚部是分开的。RML2016.10b数据集是使用GNU无线电动态信道模型分层块构建的，其中包括采样率偏移、中心频率偏移、选择性衰落和加性高斯白噪声等阻碍效应。每个调制信号有信噪比为-20～18 dB，增量为2 dB。将实验数据集按6∶2∶2随机选择为训练集、验证集和测试集。损失函数是分类交叉熵，优化器为Adam，网络训练的批量大小（batch size）为1 024，训练轮数（epoch）为1 000。实验设置若验证损失在50个epochs内未减少，则停止训练过程。

3.2 仿真环境设置

仿真环境设置如表3所示。

3.3 实验结果

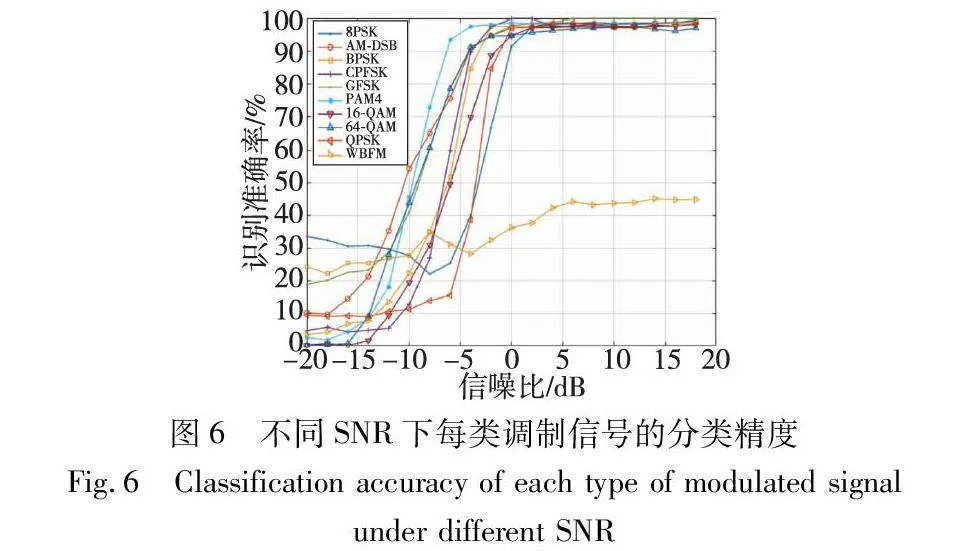
图6表示了在不同SNR下每类调制信号的分类识别准确率。从图中可以得知，不同调制信号在相同信噪比下性能有所不同。在信噪比较低时，AM-DSB的识别精度明显高于其他调制方式。在-4 dB时PAM4、QAM64、GFSK三种调制方式就达到90%以上，PAM4甚至达到了98%。0 dB下除WBFM，其他调制信号的识别精度均达到90%以上，随着信噪比的增加，识别精度逐渐平稳并趋于100%。

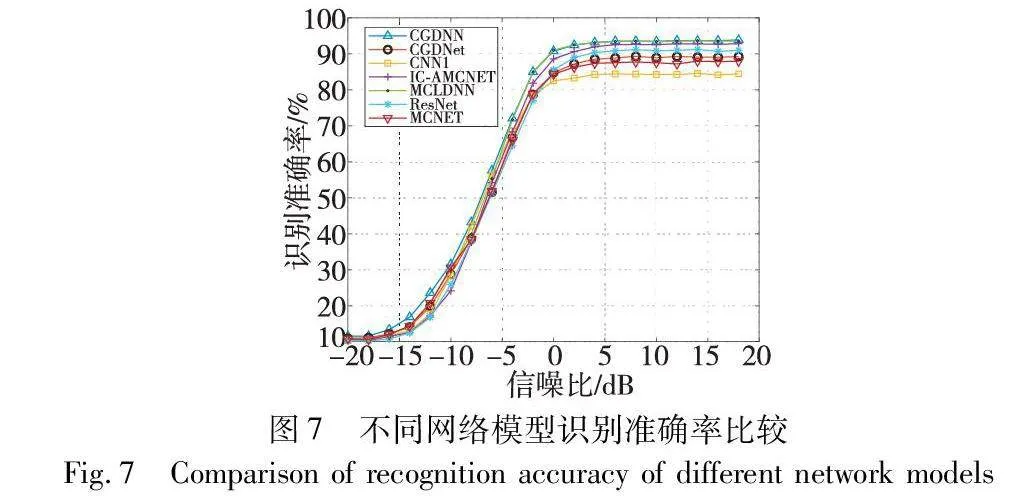
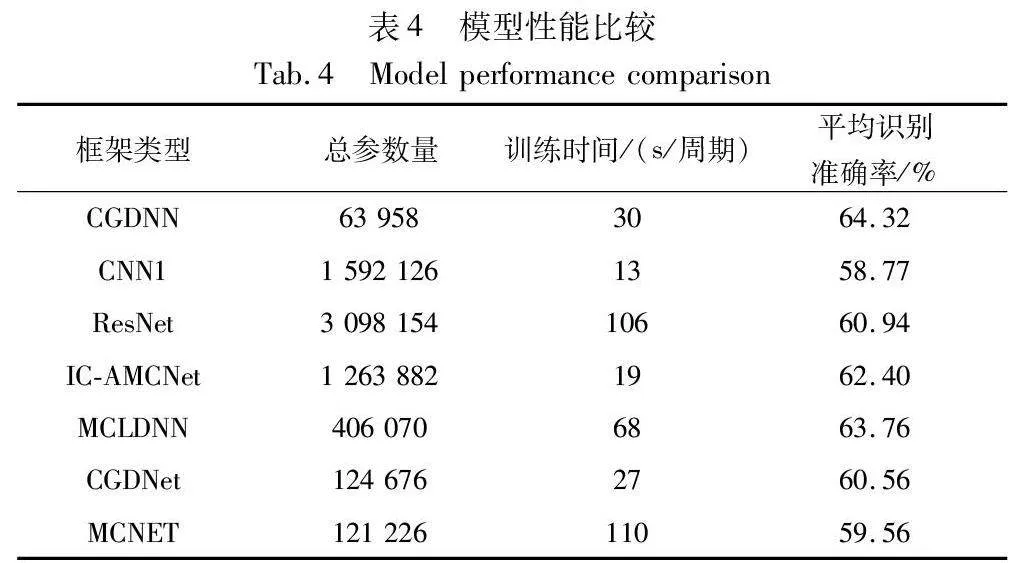
如图7所示，实验将本文的算法结构与其他几种算法进行了比较。对比实验选择CNN1［5］、IC-AMCNet［18］、MCLDNN［19］、CGDNet［20］、ResNet［21］、MCNET［22］。从图中不同网络结构的分类准确率可以明显看出，其准确率随着信噪比的增加而增加并逐渐趋于稳定。CGDNN结构的分类识别准确率整体均高于其他网络结构，在SNR为18 dB时，最大识别准确率可达93.9%，在所有对比模型中表现最好。在-18～-8 dB的低信噪比条件下，CGDNN结构的识别准确率明显优于其他网络，这也验证了小波阈值去噪方法的有效性，在低信噪比情况下对调制信号的分类识别得到了提升。在评估CGDNN性能方面，除分析其平均识别准确率之外，还可根据计算复杂度来分析评估，计算复杂度包括学习参数数量、训练时间等元素。

如表4所示，可以了解到CGDNN模型参数数量在远小于其他网络模型的情况下，平均识别准确率得到了不同程度的提升。尽管CGDNN模型训练时间大于CNN1、IC-AMCNet和CGDNet，但随着参数数量大幅减少且识别准确率的提高，CGDNN训练时间是可以接受的。与MCLDNN基准高精度模型相比，在降低模型计算复杂度和训练时间的同时提高了识别精度。

3.4 去噪效果分析

表5比较了-12 dB、-10 dB、-8 dB、-6 dB、-4 dB、-2 dB和0 dB下不同模型的调制识别结果。可以看出，CGDNN与除MCLDNN的其他模型在低信噪比下最大依次增加了6.8%、7.42%、5.47%、6.51%、7.66%、7.96%。在0 dB时识别精度小于MCLDNN模型0.27%，但CGDNN架构在低信噪比下整体表现比MCLDNN更好。根据实验所得结果，低信噪比下的识别准确率有了一定幅度的提高，也说明了提出的小波阈值去噪方法对调制信号的去噪有较好的效果。

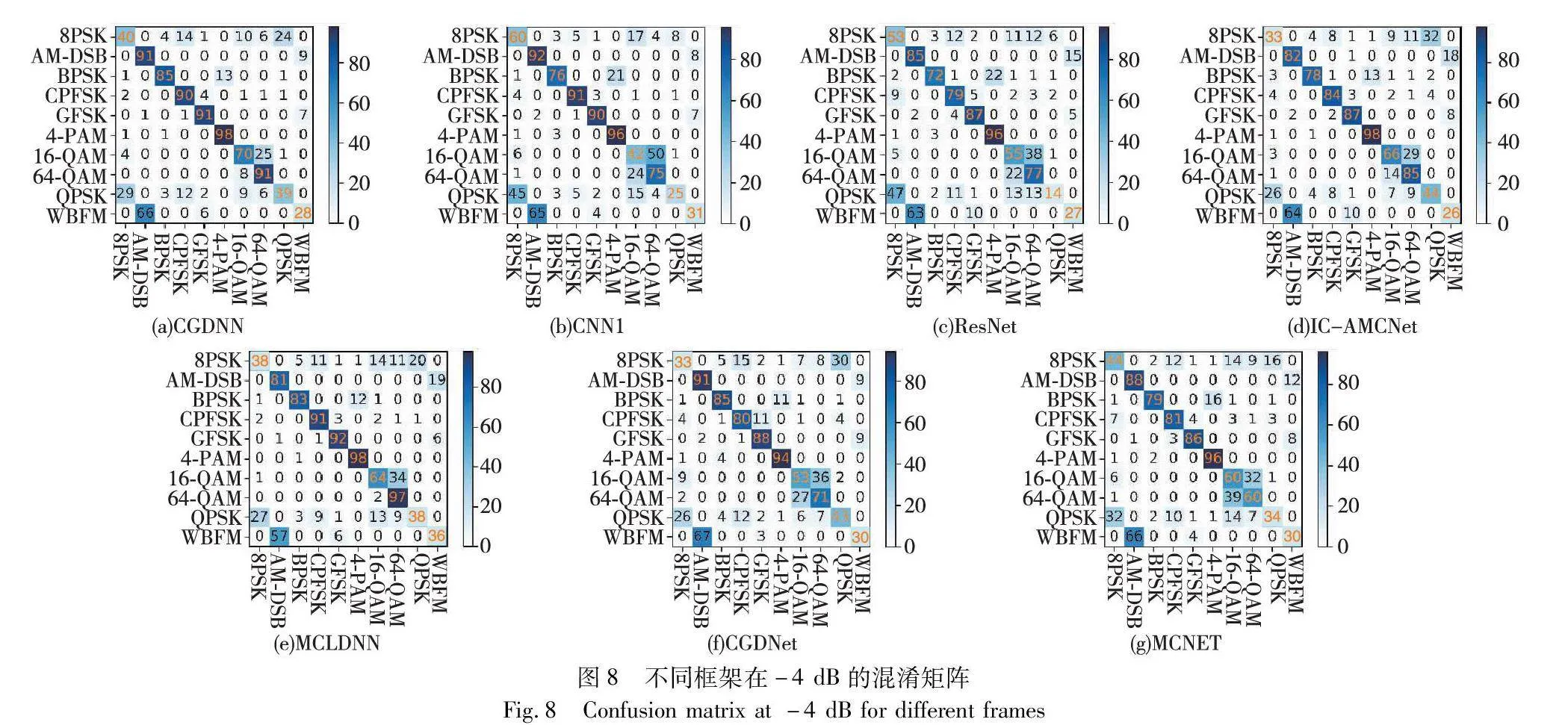
图8显示了信噪比为-4 dB条件下，不同网络模型的混淆矩阵。混淆矩阵表示不同调制格式的错误分类，预测精度越高，对角线上的结果越高，对应的蓝色也会越深（参见电子版），显示了预测标签与实际标签的一致程度。因为AM-DSB和WBFM都有一个静默期，在静默期间信号几乎为零，网络只能对无效的信号进行随机分类，所以从图中可以看出，调制格式的错误分类主要在AM-DSB和WBFM之间。CGDNN对这两类调制格式的预测精度是明显优于ResNet和IC-AMCNet模型的。CGDNN在低信噪比下相比其他模型提升了大多数调制格式的分类性能。例如，BPSK、CPFSK和GFSK的识别准确率分别为85%、90%和91%，与其他六种模型分类性能相比最大提高了13%。除此之外，16QAM与64QAM也很容易混淆，因为其调制类型非常相似，在进行分类识别时很难区分。在对I/Q样本进行小波阈值去噪之后减小了对调制类型的噪声影响，CGDNN模型准确识别了70%的16QAM与91%的64QAM，两者之间的混淆显著减少，超过了其他模型对这两种调制类型的识别能力。

4 结束语

为了解决低信噪比下自动调制识别准确率的问题，本文先对数据进行小波阈值去噪，通过利用软阈值函数进行自适应阈值调整，消除对采样的I/Q数据样本的噪声影响，从而降低在低信噪比下噪声对调制格式识别的阻碍。然后，使用CGDNN对去噪后的调制信号进行识别。该网络由CNN、GRU和DNN组成。CNN和GRU分别提取信号的空间特征和时间特征，最后由DNN对提取特征后的调制信号进行分类。通过这种方法，实现了高精度分类性能，提高了低SNR情况下的自动调制识别准确率。从RML2016.10b数据集的实验结果来看，实现了高精度分类识别，最高识别准确率达到了93.9%，在低信噪比下，信噪比为-12～0 dB时的自动调制识别准确率提升为0.36%～8.44%，同时也大大降低了计算复杂度和训练时间。未来计划继续在现有模型基础上融合更多特征，以进一步提高各种调制类型在低信噪比下的分类性能。

参考文献：

［1］Ji Mingrui， Huang Chenzhao， Luo Ruisen. Automatic modulation recognition based on spatio-temporal features fusion［C］//Proc of the 12th IEEE International Conference on Electronics Information and Emergency Communication. Piscataway， NJ： IEEE Press， 2022： 89-93.

［2］Zhang Fuxin， Luo Chunbo， Xu Jialang， et al. An autoencoder-based I/Q channel interaction enhancement method for automatic modulation recognition［J］. IEEE Trans on Vehicular Technology， 2023， 72（7）： 9620-9625.

［3］周宇航， 侯进， 李嘉新， 等. 基于频域叠加和深度学习的频谱信号识别［J］. 计算机应用研究， 2023， 40（3）： 874-879. （Zhou Yuhang， Hou Jin， Li Jiaxin， et al. Spectrum signal identification based on frequency-domain superposition and deep learning［J］. Application Research of Computers， 2023， 40（3）： 874-879.）

［4］Tunze G B， Huynh-The T， Lee J M， et al. Sparsely connected CNN for efficient automatic modulation recognition［J］. IEEE Trans on Vehicular Technology， 2020，69（12）： 15557-15568.

［5］O’Shea T J， Corgan J， Clancy T C. Convolutional radio modulation recognition networks［C］//Proc of the 17th International Conference on Engineering Applications of Neural Networks. Cham： Springer， 2016： 213-226.

［6］Daldal N， Yldrm ， Polat K. Deep long short-term memory networks-based automatic recognition of six different digital modulation types under varying noise conditions［J］. Neural Computing and Applications， 2019， 31： 1967-1981.

［7］West N E， O’shea T. Deep architectures for modulation recognition［C］//Proc of IEEE International Symposium on Dynamic Spectrum Access Networks. Piscataway， NJ： IEEE Press， 2017： 1-6.

［8］Huang Sai， Dai Rui， Huang Juanjuan， et al. Automatic modulation classification using gated recurrent residual network［J］. IEEE Internet of Things Journal， 2020， 7（8）： 7795-7807.

［9］Rodzin S， Bova V， Kravchenko Y， et al. Deep learning techniques for natural language processing［M］//Artificial Intelligence Trends in Systems. Cham： Springer， 2022： 121-130.

［10］Gao Yan， Ma Shengyu， Shi Jian， et al. An optimised multi-channel neural network model based on CLDNN for automatic modulation recognition［J］. International Journal of Wireless and Mobile Computing， 2023， 24（2）： 144-158.

［11］Donoho D L. De-noising by soft-thresholding［J］. IEEE Trans on Information Theory， 1995， 41（3）： 613-627.

［12］Halidou A， Mohamadou Y， Ari A A A， et al. Review of wavelet denoising algorithms［J］. Multimedia Tools and Applications， 2023， 82： 1-31.

［13］吴光文， 王昌明， 包建东， 等. 基于自适应阈值函数的小波阈值去噪方法［J］. 电子与信息学报， 2014， 36（6）： 1340-1347. （Wu Guangwen， Wang Changming， Bao Jiandong， et al. Wavelet threshold denoising method based on adaptive threshold function［J］. Journal of Electronics and Information， 2014， 36（6）： 1340-1347.）

［14］Zhang Fuxin， Luo Cunbo， Xu Jialang， et al. An efficient deep lear-ning model for automatic modulation recognition based on parameter estimation and transformation［J］. IEEE Communications Letters， 2021， 25（10）： 3287-3290.

［15］Liu Xingyu， Zhen Zonglei， Liu Jia. Hierarchical sparse coding of objects in deep convolutional neural networks［J］. Frontiers in Computational Neuroscience， 2020， 14： 578158.

［16］Chen Junjia， Pan Zhibin. Saturated non-monotonic activation functions［EB/OL］. （2023-05-25）. https：//arxiv.org/abs/2305.07537.

［17］O’shea T J， West N. Radio machine learning dataset generation with GNU radio［C］//Proc of the 6th GNU Radio Conference. 2016： 69-74.

［18］Hermawan A P， Ginanjar R R， Kim D S， et al. CNN-based automa-tic modulation classification for beyond 5G communications［J］. IEEE Communications Letters， 2020， 24（5）： 1038-1041.

［19］Xu Jialang， Luo Chunbo， Parr G， et al. A spatiotemporal multi-channel learning framework for automatic modulation recognition［J］. IEEE Wireless Communications Letters， 2020，9（10）： 1629-1632.

［20］Njoku J N， Morocho-Cayamcela M E， Lim W. CGDNet： efficient hybrid deep learning model for robust automatic modulation recognition［J］. IEEE Networking Letters， 2021， 3（2）： 47-51.

［21］Liu Xiaoyu， Yang Diyu， El Gamal A. Deep neural network architectures for modulation classification［C］//Proc of the 51st Asilomar Conference on Signals， Systems， and Computers. Piscataway， NJ： IEEE Press， 2017： 915-919.

［22］Zhang Fuxin， Luo Cunbo， Xu Jialang， et al. Deep learning based automatic modulation recognition： models， datasets， and challenges［J］. Digital Signal Processing， 2022， 129： 103650.