基于三角网算法的公路纵断面设计及实例验证

摘要：针对当前公路纵断面设计结果与真实施工环境数据拟合度较差，其应用效果不佳。为此，提出基于三角网算法的公路纵断面设计方法，并通过实例验证此方法应用效果。首先，根据车辆行驶参数统计分析结果，确定公路基础设计参数；其次，构建基础三维模型，将该模型与研究区域的基础三角网图合并，得到三角网计算模型；最后，应用模型计算结果，完成公路纵断面设计方案，确定关键设计参数。实验结果表明：基于三角网算法的公路纵断面设计结果与真实施工环境数据拟合度更高。

关键词：三角网算法公路纵断面市政交通工程道路施工

中图分类号：U491

Highway Profile Design and Its Case Verification Based on the Triangulation Algorithm

ZHANG Dongning

Gansu Zhongping Engineering Design & Consulting Co.，Ltd.，Lanzhou， Gansu Province，

730060China

Abstract：At present， the result ofhighway profile design has a lowerdegree of fitting with the data of the real construction environment， and its application effect is not good. Therefore， amethod of highway profile design based on the triangulation algorithm is proposed， and the application effect of this method is verified by examples. Firstly， thebasic design parameters of highways are determined according to the statistical analysis results of vehicle driving parameters. Then， a basic 3D model is constructed， and the model is combined with the basic triangulation diagram of the research area to get a triangulation calculation model. Finally， the scheme of highway profile design is completed by the calculation results of the model， and key design parameters are determined. Eexperimental results show that the result of highway profile design based on the triangulation algorithm has a higher degree of fitting with the data of the real construction environment.

Key Words： Triangulation algorithm; Highway profile; Municipal traffic engineering; Road construction

随着城市交通与公路建设工程的发展，在公路设计的过程中，实现的交通量往往低于设计量[1]。当前，公路纵截面设计当前多采用线形拟合的方法，通过数值计算对研究区域的地形进行初步拟合，但此部分方法存在计算结果精准度较低的问题[2]。因此，如何通过数据处理，得到更为可靠的公路纵断面设计结果成为当前需要解决的重点问题[3]。对比多种方法后，本研究选取三角网算法对当前可使用的方法展9UM6xE6hdKYYeEYmtkxgDg==开优化，提出基于三角网算法的公路纵断面设计方法，力求通过此方法改善当前公路施工设计过程中存在的问题。

1基于三角网算法的公路纵断面设计

1.1车辆行驶参数统计分析

公路纵断面设计参数主要受到车辆行驶阻力的影响[4]。为考虑到车辆行驶的安全性，本次研究中增加空气阻力，提升数据的多样性，以此在保证纵断面设计结果的同时，降低行车安全问题。

首先，根据空气重力学的相关理论[5]，计算车辆行驶过程中的空气阻力。计算过程可表示为如下所示：

（1）

式（1）中： 表示空气密度； 表示车辆的迎风面积； 表示风阻系数； 表示车辆的行驶速度。

其次，在确定空气阻力 的基础上，对车轮的滚动阻力展开计算，具体计算过程设定如式（2）：

（2）

式（2）中， 表示车轮的滚动阻力； 表示车辆的总重力； 表示车轮的滚动系数； 表公路的坡道倾角。

最后，在上述内容的基础上，增加惯性阻力计算式（3）：

（3）

式（3）中： 表示重力加速度； 表示车辆的加速度； 表示惯性力系数。通过此公式，可计算得出车辆在目标路段的惯性参数，进一步获取车辆安全行驶的性能数据。

1.2构建公路纵断面三角网计算模型

为更好地处理公路纵断面复杂区域的数值，得到更优的设计结果。应用获取到的数据构建基础三维模型，而后将制图区域按照“最优辅助划分原则[6]”进行区域划分，并尽可能减少子区域的误差，将划分后的区域整合为由内向外发展的拓扑结构。与此同时，将此模型与研究区域的基础三角网图合并，得到本次研究中需要的三角网地形图。因此，根据以上原理，三角网计算模型的构建步骤设定如下。

步骤1：确定研究区域属性。通过三角网算法确定目标区域的二维情况，并将其转化为通用信息，以便于后续的区域划分。

步骤2：确定三角网算法计算流程，完成研究区域由左到右转存到链表中，构建基础拓扑结构。

步骤3：调用指令确定研究区域的基础属性，并进一步判定目标区域是否在三角网制图边境内，是否被处理过，以及该区域公路纵断面的断面属性以及边界情况。

步骤4：约束区域边界以及制图边界，如此两部分边界封闭较多，则需要应用“三角形生长法”对其进行处理，并将其存储在链表中进行编号。

步骤5：重新建立全部区域的拓扑结构，进行区域重组，得到最终的三角网模型。

假设制图区域内有N个离散数据点，则三角网算法寻找扩展点的流程如图1所示。

将得到的三角网模型作为计算基础，为保证其应用效果，在使用前需确定三角网中的几何图形是否一致，同时保证拓扑结构具有稳定性。如此三角网模型符合计算要求，则将其作为纵断面设计过程中的模型基础，应用其完成最终纵断面设计。

1.3公路纵断面设计

应用上述内容的设计结果，完成公路纵断面设计方案。对比多种文献后，使用下述公式获取基础设计数据。

1.3.1 路纵截面设计高程

（4）

式（4）中： 表示研究区域内任意点里程桩号的设计高程； 表示里程桩起点设计高程； 表示里程桩号 与 之间的距离； 表示纵坡值，当坡度为上坡是取值为正，当坡度为下坡是取值为负。

1.3.2 挖设计高度

（5）

式（5）中， 表示地基高程。

1.3.3 路纵断面竖曲线

（6）

式（6）中： 表示目标位置的水平定位数据； 表示竖曲线半径； 表示目标位置的竖直定位数据。其计算方式如下：

（7）

整理上述各参量，结合三角网计算模型，得到最终具有地形特征的公路纵断面设计结果。

2实例验证分析

2.1工程实例

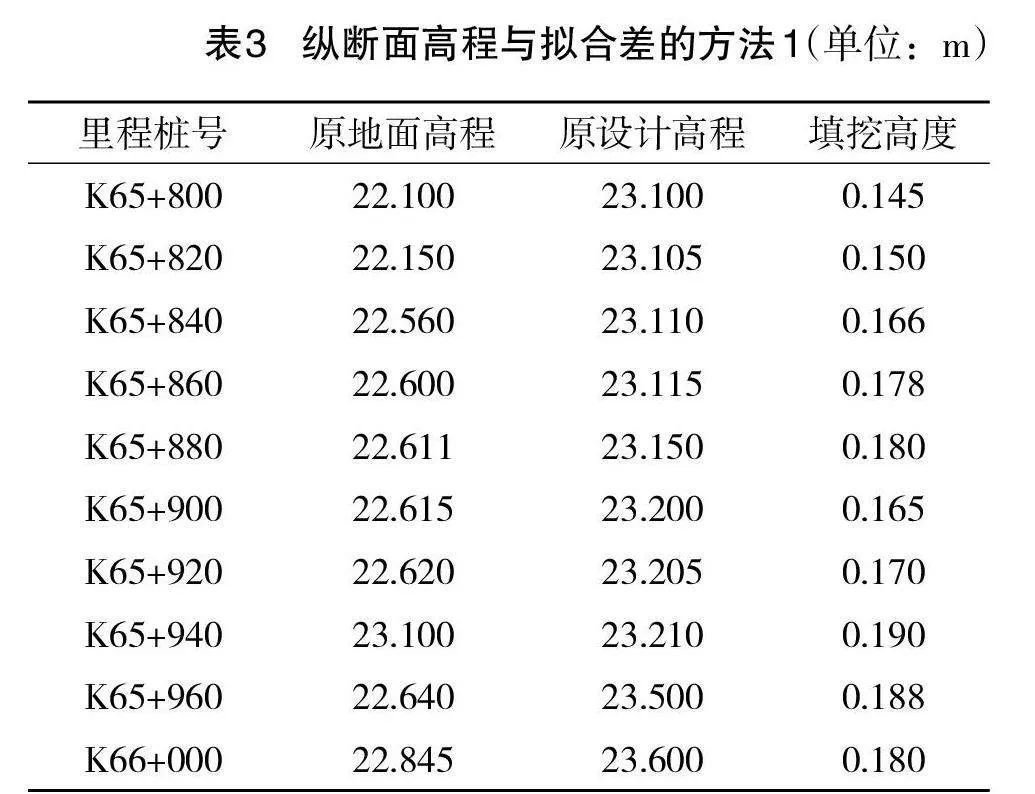
本研究以城市某公路扩改建工程为例，获取部分公路段设计资料，其中：纵坡度I1=0.15%，横向坡度I2=-0.12%，原设计曲线Y=128000m，L=360.64m。在公路的扩建设计与改建设计中，需要降低填挖高度，使得设计线与原地面曲线得到更好的拟合。针对此设计目标，使用文中方法文献方法1、文献方法2分辨设计方案，并对比应用效果。为获取更为有效的实验结果，本次研究中选取10个里程桩作为测试组，获取原始地面高程、设计高程以及填挖高度拟合差数据，具体如表1所示。

将表1中数据作为对照，为后续的实验对比分析提供数据基础。通过数据对比的形式，得到文中方法和两种文献方法的应用效果。

2.2实验结果分析

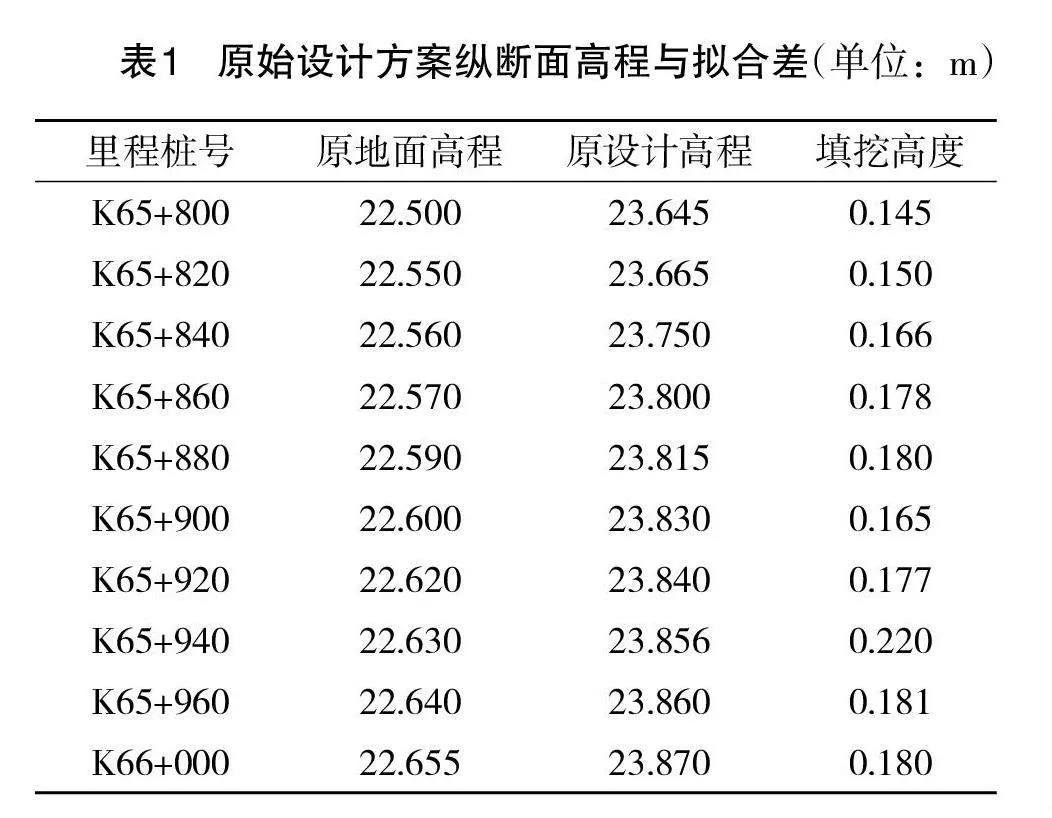
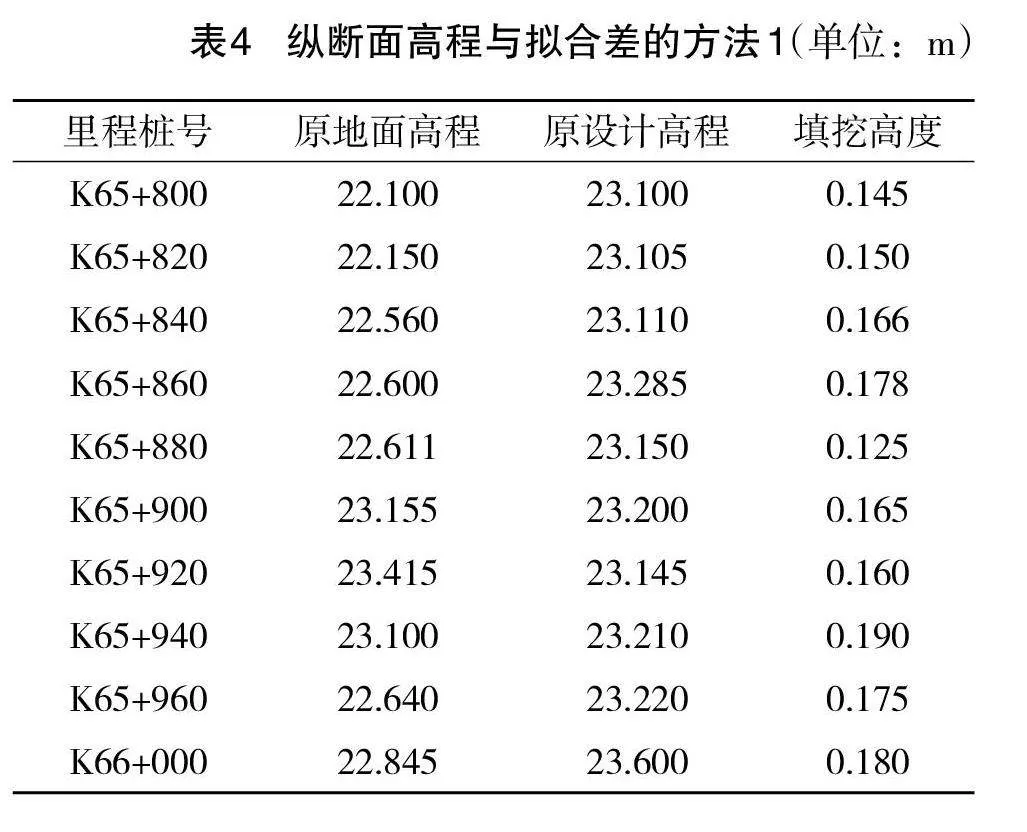
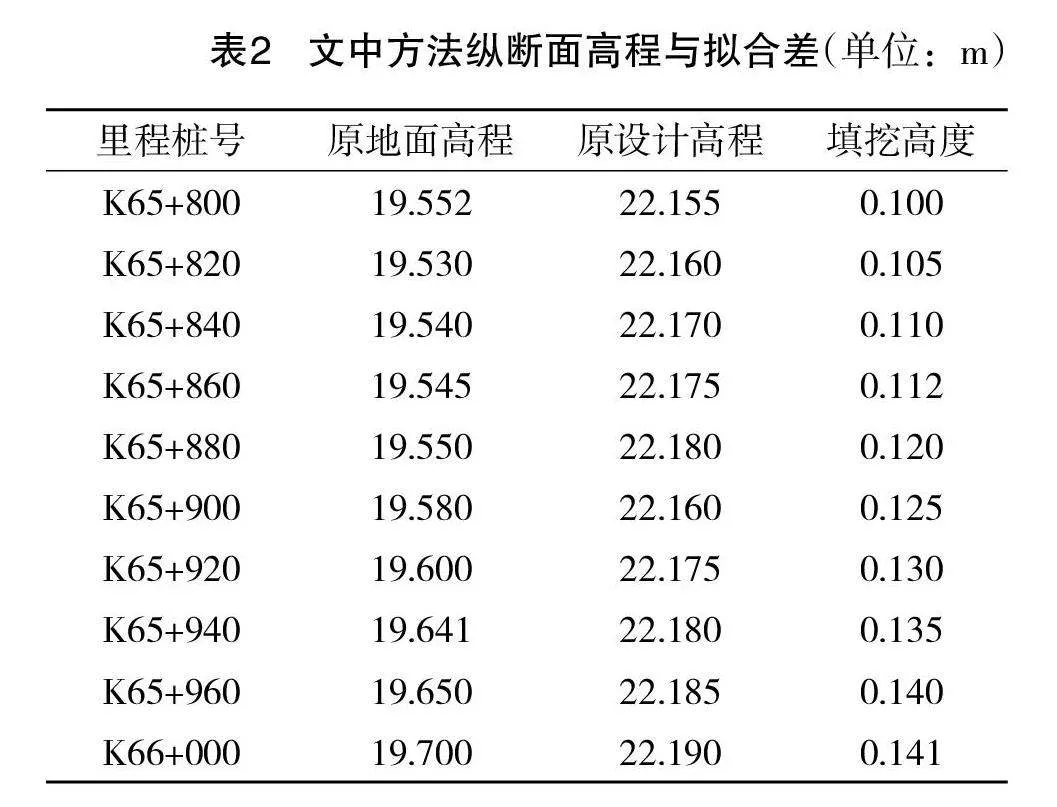
根据上述实验方案，得到如表2至表4所示的实验数据。

将表2至表4中的数据与表1中的数据进行对比可以看出，实验中选择的3种方法均可完成纵截面的基础设计，但设计结果与真实地面高程的拟合度存在较大的差异。与文中方法相比，文献中的两种方法计算耗时相对较长，且计算结果拟合差明显高于文中方法，虽然解决了部分数据拟合过程中存在的问题，但应用效果相对较差。整理上述实验结果可以确定，文中方法的应用效果更佳，可更好地成公路路基的纵截面设计工作。

3结语

综上，经过深入的探讨和实例验证，在实际应用中，本研究选取了典型的公路项目作为案例，进行了详尽的数据分析和处理。通过与其他设计方法的对比，发现基于三角网算法的纵断面设计拥有更高的应用价值，为公路建设的可持续发展做出了积极贡献。此外，本研究还对算法进行了优化和改进，提高了其计算效率和稳定性。这使得基于三角网算法的纵断面设计在实际工程中更具可操作性，能够更好地满足项目需求。

参考文献：

[1]梁建文，官其铝，李东桥，等.地下预制管廊纵断面抗震设计的反应位移法[J].地震工程与工程振动，2023，43（6）：159-166.

[2]陈正委，熊文磊，高升，等.轻型高速公路代表性车型与纵断面设计指标研究[J].公路，2023，68（9）：1-11.

[3]何庆，徐双婷，高天赐，等.线路关键点对400km/h高速铁路纵断面参数设计影响[J].铁道工程学报，2022，39（11）：25-32.

[4]尤磊，晏成名，宋新宇.自适应二分的并行Delaunay三角网生长算法[J].信阳师范学院学报（自然科学版），2022，35（4）：656-663.

[5]许浒，邹鹏，余志祥，等.山区公路高陡边坡引导式柔性缓冲系统的设计方法[J].中国公路学报，2022，35（9）：235-246.

[6]李帅.高速铁路车站两端平纵断面设计参数匹配及检算研究[J].铁道标准设计，2022，66（4）：25-29.