基于电测法测量弹性模量和泊松比的实验研究

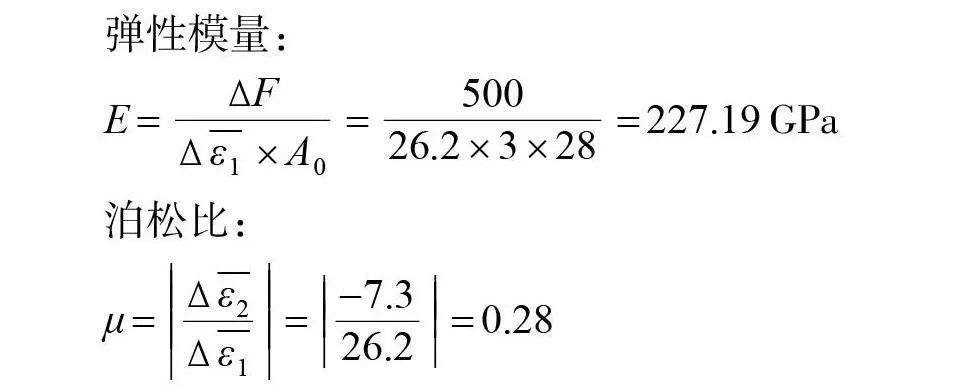
摘要：测量材料的弹性模量和泊松比是材料力学实验的一项重要实验项目。为了丰富材料力学实验教学手段和教学内容，把理论计算、有限元仿真技术和电测法测试技术有机的融合在一起。分别通过电测法、ABAQUS软件模拟和理论计算方法得到低碳钢的弹性模量和泊松比。结果表明：模拟结果和理论计算结果几乎相等，但是电测法实验测试结果与理论计算结果之间的误差相对较大，主要是由于电阻应变片在试样表面的黏贴质量不高和试样的几何尺寸测量不精确造成的。

关键词：电测法ABAQUS软件 弹性模量 泊松比材料力学实验

中图分类号：TB302.1

AnExperimental Study on the Measurement of the Elastic Modulus and Poisson's Ratio Based on the Electrical Measurement Method

CHEN Hongbing HU Libang YAO Liping LI Li

College of Engineering and Technology， Southwest University， Chongqing，400715 China

Abstract：Measuring the elastic modulus and Poisson's ratio of materials is an important experimental project inExperimentsofMechanics ofMaterials. In order to enrich the teaching methods and teaching contents of Experiments ofMechanics ofMaterials， theoretical calculation， finite element simulation technology and electrical measurement testing technology are organically integrated， andthe elastic modulus and Poisson's ratio of low-carbon steel are obtained by electrical measurement， ABAQUS software simulation and theoretical calculation methods. The results show that simulation results are almost equal to theoretical calculation results， but the error between the experimental measurement results of the electrical measurement method and the resultsof theoretical calculation is relatively large， which is mainly caused by the poor bonding quality of the resistance strain gauge on the surface of the sample and the inaccurate measurement of the geometricdimension of the sample.

Key Words：Electrical measurement method; ABAQUS software; Elastic modulus; Poisson's ratio; Experiments ofMechanics of Materials

目前，很多高校的材料力学实验不管是在教学内容上还是在教学方法上都没有得到长足发展，主要原因：（1）材料力学实验项目依附于理论课，新的理论没有增补进教材，导致实验项目更新缓慢；（2）学时数缩减，无法充实更多的实验项目；（3）经费缺乏，实验设备更新缓慢；（4）教学方法没有得到根本性的改进，实验课仍然以讲授和演示为主[1]。因此，实验课的吸引力不足，学生的学习积极性不高。为了改变这种状况，实验项目应具有一定的前沿性和挑战性，教学手段应具有一定的先进性和互动性。将有限元分析技术引入教学过程中有利于激发学生兴趣，使实验课变得生动形象，培养和锻炼学生解决复杂工程问题的能力。已有一些学者利用有限元仿真技术辅助实验教学，例如：苑霄雯等人[2]利用ANSYS软件模拟了低碳钢的拉伸实验；王国明等人[3]利用ANSYS软件模拟了矩形截面梁的纯弯曲实验；张建勋等人[4]利用ABAQUS软件模拟得到的各种应力、应变云图，直观、形象地解释了材料力学的基本概念和材料的变形过程；赵通来等人[5]利用ABAQUS软件模拟了飞机起落架的结构强度，对起落架的结构设计和轻量化减重进行了优化分析。从以上文献可以看出，ABAQUS 有限元分析软件在材料力学实验教学和工程实践方面都有广泛应用。

1测量弹性模量和泊松比的实验原理

1.1弹性模量的概念及测试方法简介

弹性模量E和泊松比μ是表征材料力学性能的两个重要参数，开发一种新材料或者实际工程应用中均需要知道这两个参数，才能够确保材料的安全使用。从微观上来讲，弹性模量是由材料内部的原子与原子之间的结合力强弱决定的，是反映材料的内在本质特征参数[6]。材料的晶体结构类型、晶体的点阵间距、孔隙率等都是其重要影响因素。从宏观上来讲，弹性模量E是表征材料抵抗弹性变形能力的指标。一般而言，E越大，材料产生弹性变形所需的应力就越大，弹性变形就越困难，反之则反。工程上常把E称作材料的刚度。

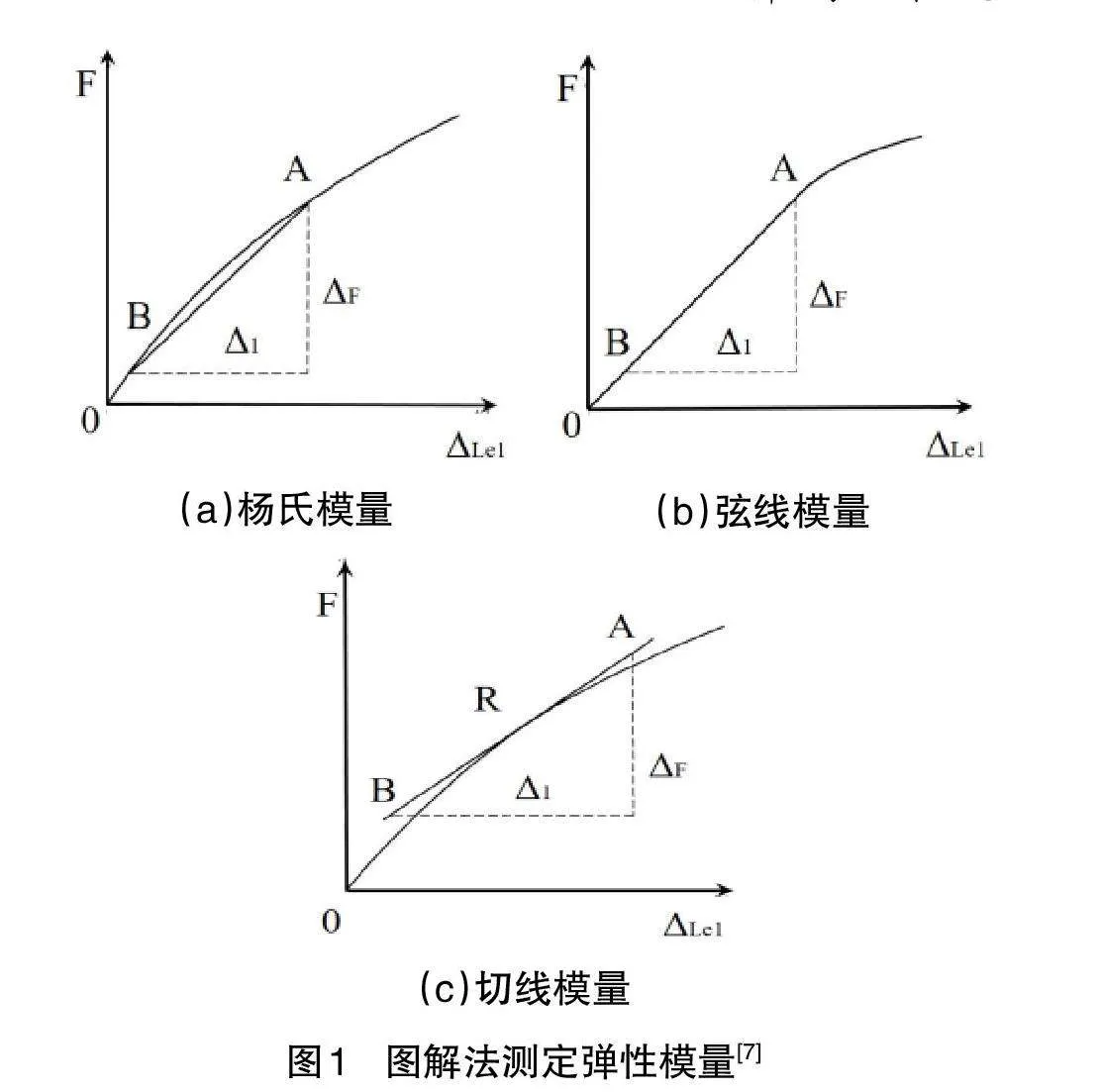
随着科学技术的不断进步，测定弹性模量的方法多达十余种，涉及的实验原理和技术手段各不相同。根据国家标准《金属材料 弹性模量和泊松比试验方法》（GB/T 22315—2008）可知测量弹性模量主要有静态法和动态法两类方法[7]。其中，静态法是指对试样施加轴向力，在其弹性范围内测定相应的轴向变形和横向变形，然后计算求解弹性模量和泊松比，通过图解法和数据拟合法进行数据处理。常用的静态测量法有引伸计测量法和电测法等。然而，在材料力学实验教学过程中，使用电测法更易于实施实验教学和提高学生的感性认识和实验的可操作性。测定弹性模量的图解法有3种[7]：（1）通过在测得的轴向力-轴向变形曲线上确定一段直线段，然后在该直线段上选取A、B两点，A、B两点的纵坐标和横坐标的增量之比即为杨氏模量，如图1（a）所示；（2）通过在测得的轴向力-轴向变形曲线上，通过与所规定的上、下两应力（或应变）点A、B画一条弦线，该弦线的斜率即为弦线模量，如图1（b）所示；（3）通过在测得的轴向力-轴向变形曲线上，然后通过规定应力（或应变）值对应的R点作曲线的切线，该切线的斜率即为切线模量，如图1（c）所示。

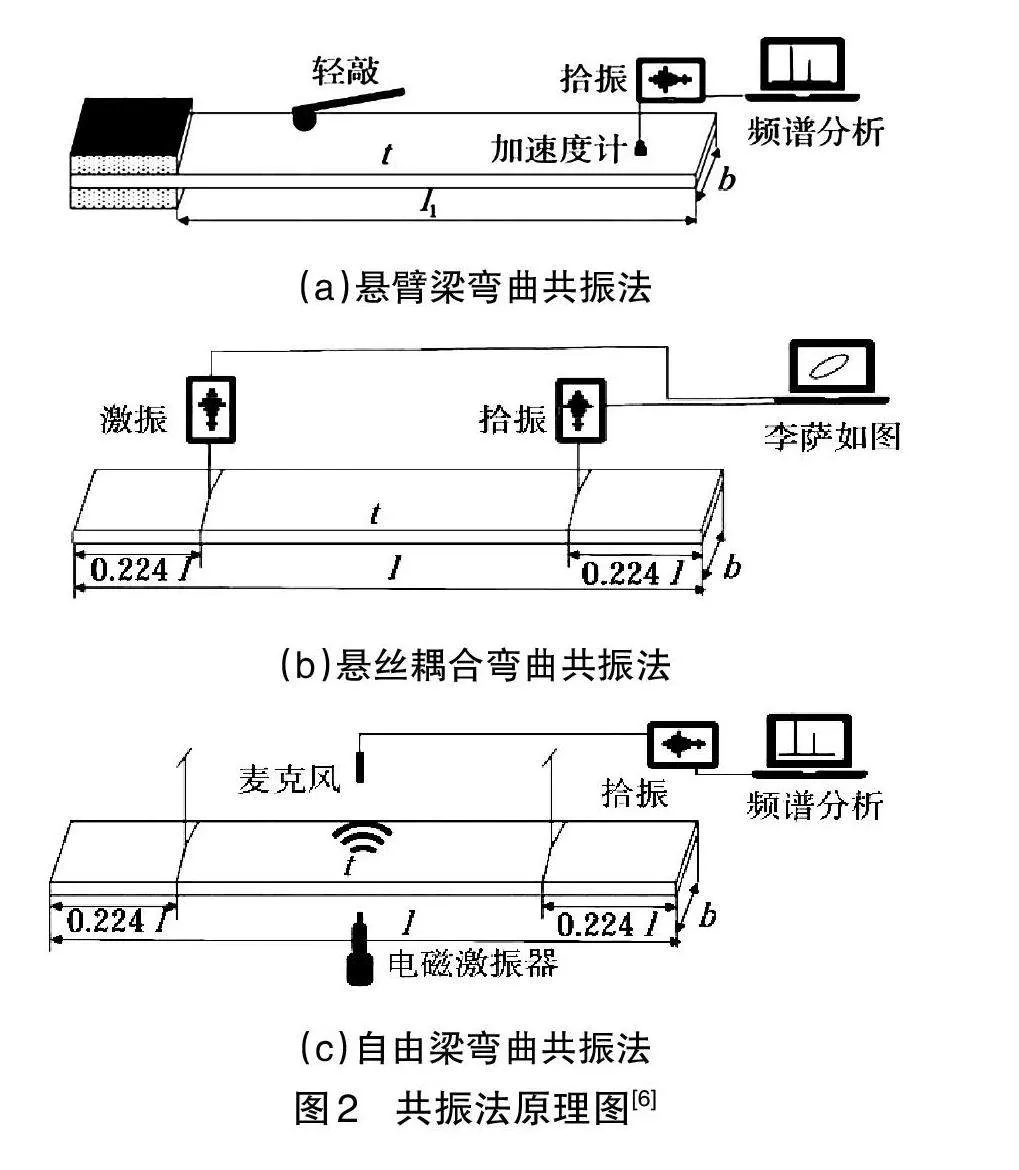
动态法（或共振法）主要是指依据声共振原理测定试样的机械共振频率，以便测定动态弹性模量、动态切变模量和动态泊松比等[7]。共振法[6]可以分为悬丝耦合弯曲共振法、单悬臂弯曲共振法和自由梁弯曲共振法等，如图2所示。一般推荐采用悬丝耦合共振法，它具有振幅大，共振易判定，振动长度易测定，温度适用范围广等优点。

1.2基于电测法测量弹性模量和泊松比的实验方法

在材料力学实验中，通常采用电测法来测试材料应变的大小，它的基本原理是将高灵敏度的电阻应变片用胶水牢固地黏贴在光滑的被测构件表面[8]。应变片将随构件一起变形，应变片变形后其电阻值改变，应变片电阻值改变将破坏测试电桥的平衡，从而输出电流（或者电压），然后换算成应变值，最后根据胡克定律就可得到应力值。电测法具有测量精度高、应用范围广和影响小等优点。

当试样受到轴向拉伸时，根据材料体积不变原则，试样的轴向伸长必然引起横向收缩。若轴向应变为ε_1，横向应变为ε_2；二者之比为一常数，其绝对值称作横向变形系数，又称泊松比，用μ来表示。当试样受到轴向拉伸时，就会产生弹性变形，通过应变仪可以测得轴向应变和横向应变。试样的横截面面积为A0，施加的载荷为 F，则可计算得出弹性模量 E和泊松比μ为：

E=σ/ε_1 =F/（ε_1×A_0 ）（1）

μ=|ε_2/ε_1 |（2）

为了验证应力与应变的线性关系，一般采用增量法，逐级加载。如果在各次载荷增量△F 作用下，测得相应的应变增量基本相同，就可以验证虎克定律的正确性。假定各次测得∆ε_1和∆ε_2的平均值分别为∆¯（ε_1 ）和∆¯（ε_2 ），则弹性模量和泊松比又可表达为：

E=∆F/（∆¯（ε_1 ）×A_0 ） μ=|（∆¯（ε_2 ））/（∆¯（ε_1 ））|（3）

2 ABAQUS软件模拟分析

ABAQUS 软件是一款功能强大的有限元分析软件，它既能分析简单的线性静力学问题，又能解决复杂的非线性问题[6，7]。本实验的模拟分析流程如下。

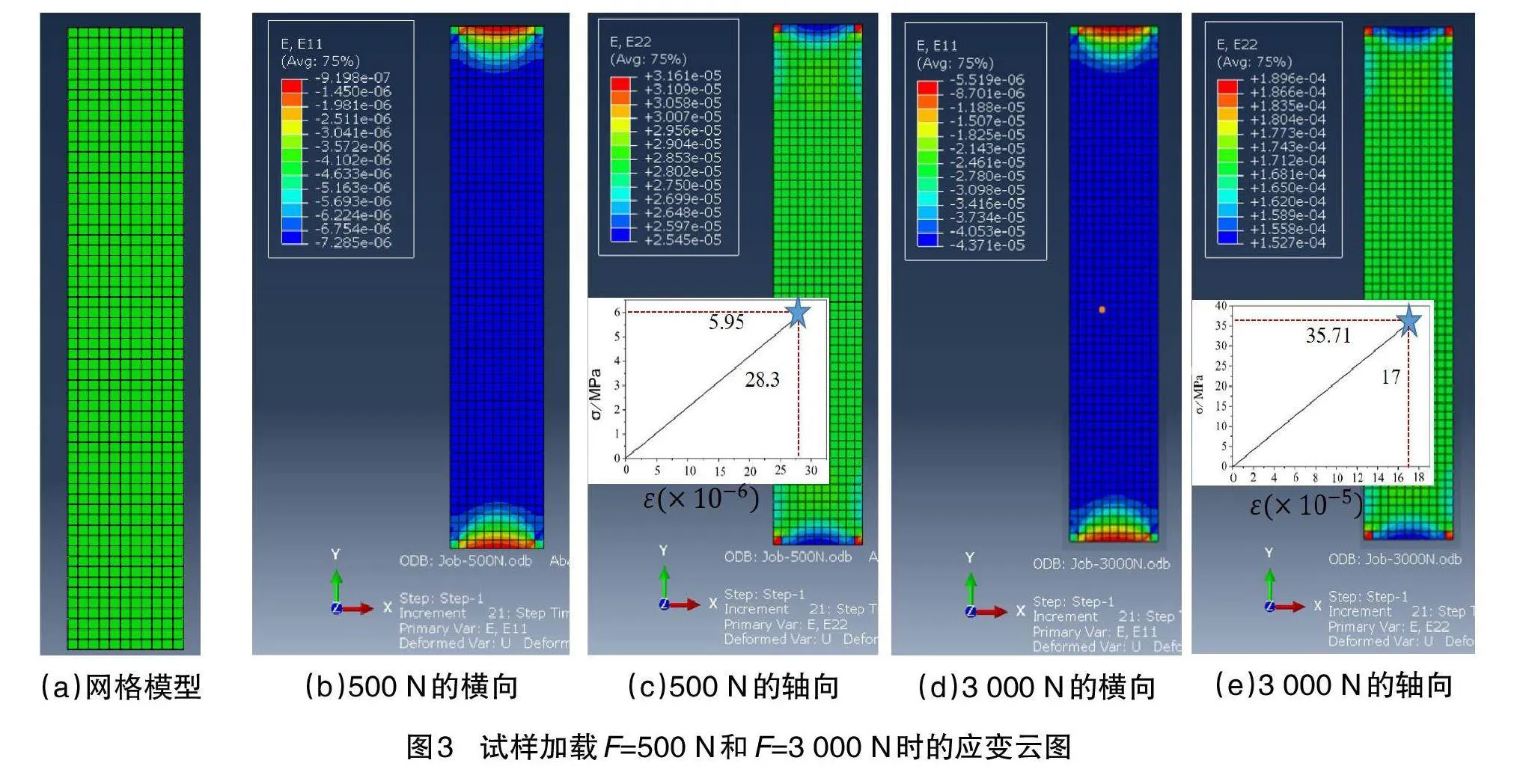
（1）建立仿真模型。利用ABAQUS软件绘制试样的三维模型，试样长为150mm， 宽为28mm， 厚为3mm的一个矩形截面长条试样。（2）设置参数。低碳钢 Q235，材料的弹性模量 E= 210GPa，采用线弹性材料模型。（3）分析步设置。选择静力学分析，时间设置为1，不考虑几何非线性，初始增量步设置为0.01，最小增量步为10-5，最大增量步为0.1。（4）载荷与边界条件。模型下端面加载固定约束，设置一参考点与上端面耦合，分别施加500N和3000N于参考点。（5）划分网格。设置好所有的边界条件后，对三维模型进行网格划分，网格尺寸为2.5mm，选用最常用的 C3D8R 单元类型。（6）后处理与数据分析。提交计算并等待计算完毕后，在后处理阶段显示 ODB 文件中的分析计算结果， 包括变形前后的模型图、各种变量的分布云图等。为了节省篇幅，图3仅展示了试样的网格模型图、施加500N和3000N的横向和轴向应变云图。

从图3可以看出，在试样中间区域不管是横向应变还是轴向应变均显示其变形是均匀的弹性变形。另外，试样的横向应变为压缩应变，为负值，如图3（b）和（d）所示；试样的轴向应变为拉伸应变，为正值，如图3（c）和（e）所示。在图3（c）和（e）的插图中，可以看出应力-应变呈线性相关性，即属于弹性变形，而且当F=3000N时，试样的应力和应变值与F=500N时的应力和应变值具有6倍的关系，这说明采用等增量逐级加载是可靠的，模拟结果是准确的、有效的。

3实验测试及结果分析

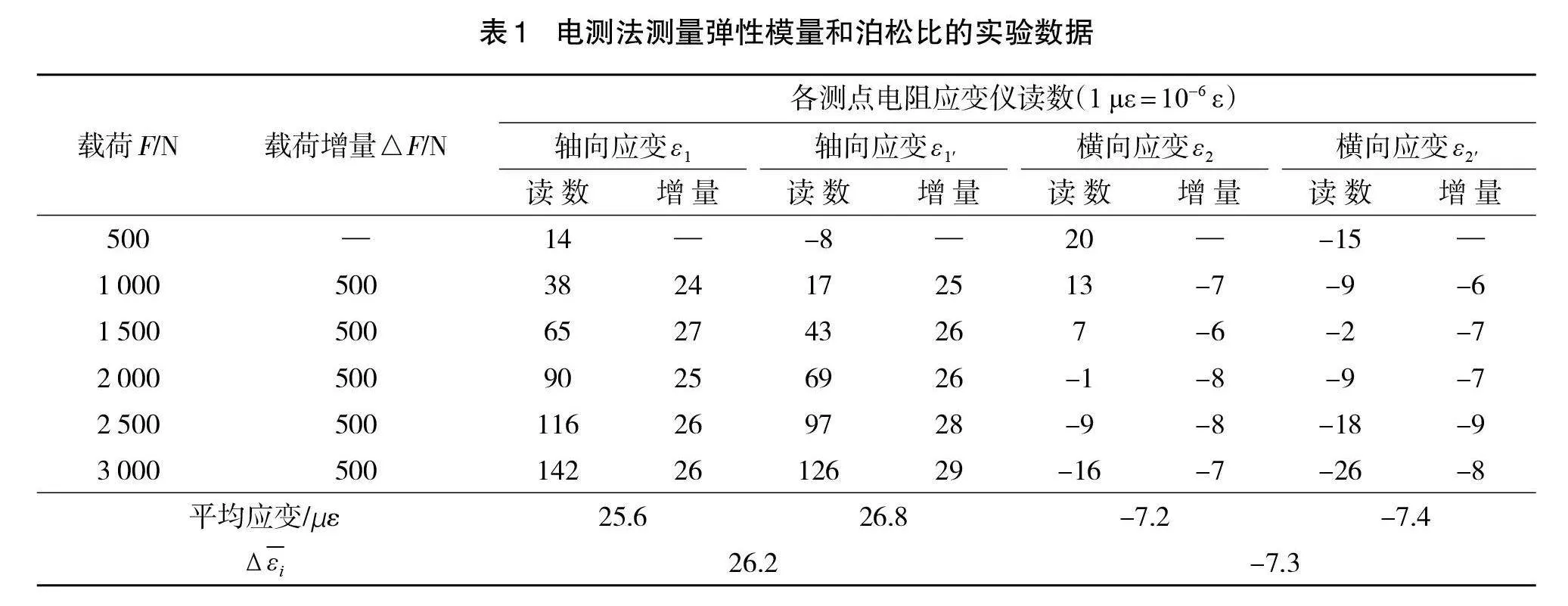
基于电测法测试低碳钢的弹性模量和泊松比的实验装置全景，如图4（a）所示。用低碳钢板材自制的实验装置，如图4（b）所示，试样的横截面尺寸为：b=28 mDsJSG2U823IqA/6hupqq6Q==m，t=3mm。在试样的正反面沿轴向和横向分别贴有应变片 R1和 R2，如图4（b）所示。当试样受到轴向拉伸时，宽度方向受到压缩变形，产生负的应变；长度方向受到拉伸变形，产生正的应变。实验采用ETM105D电子万能试验机给试样施加拉力，采用等增量逐级加载方式（∆F=500N），从500N～3000N每增加一级载荷，试验机自动停止加载，即保载30 s，以便从静态电阻应变仪上读出数据，加载曲线如图4（d）所示。实验过程由试验机程序自动控制，实验操作方便，加载力值精度高。实验采用CM-1L型静态电阻应变仪，采用半桥单臂温度补偿测量电桥连接方式，应变片电阻为120Ω，灵敏系数K=2.08，如图4（c）所示。最后，记录实验数据，如表1所示。

材料力学教材推荐的低碳钢的弹性模量E为196～216GPa，μ为0.24～0.28 的取值范围[9]。从表2可以看出，实验测得的弹性模量稍微偏高，模拟分析的弹性模量与理论计算使用的弹性模量几乎相等，说明模拟结果准确有效。另外，实验测试的泊松比和模拟的泊松比均在允许取值范围内，实验测试值稍微偏高，这可能是由于电阻应变片黏贴质量不高和试样几何尺寸测量不精确造成的。总体而言，3种数据的误差均较小，说明用这3种方法测试低碳钢的弹性模量和泊松比是可靠的、准确的。

4 结论

通过理论分析计算了低碳钢试样施加F=500N时的拉伸轴向应力和轴向应变参数；通过ABAQUS软件模拟了低碳钢试样的拉伸变形，获得了各种加载条件下的应变云图与应力-应变曲线，根据结果计算了弹性模量和泊松比；通过电测法实验测试了低碳钢的轴向应变和横向应变，计算了弹性模量和泊松比。通过对比分析3种数据，发现它们之间的误差较小，证明实验装置是可靠的，模拟分析结果是正确的。通过引入有限元分析技术，有利于丰富实验教学手段和实验教学内容，提高实验课的吸引力，激发学生的学习兴趣，为培养和锻炼学生利用力学知识和有限元分析技术解决复杂工程问题提供了强力支撑作用。

参考文献

[1] 王云洋，赵丙晨，杨光，等.基于铸铁拉伸实验的材料力学实验教学改革研究[J].大学物理实验，2019，32 （4）：103-105.

[2] 苑霄雯，彭胡，朱爽，等. 基于ANSYS的低碳钢拉伸实验与传统实验数据对比分析研究[J]. 内燃机与配件，2022 （6）：16-18.

[3] 王国明，邓立君，汤沛源. 有限元分析在材料力学实验教学中的应用[J].中国现代教育装备， 2020 （1）： 95-97.

[4] 张建勋，徐志敏，白金文. ABAQUS 软件在“工程力学”课程教学中的应用[J].装备制造技术， 2023 （8）：101-103.

[5] 赵通来，贺伟，张鸣影.基于ABAQUS的起落架结构强度分析方法[J].制造与工艺， 2023 （10）： 49-51.

[6] 余建新，崔喜平.弹性模量的实验方法比对研究[J].实验科学与技术，2020，18 （6）：14-18.

[7] 奚建法，李昕，王滨，等.金属材料弹性模量和泊松比试验方法：GB/T 22315—2008 [S].北京：中国标准出版社，2008.

[8] 汤占岐，武美先，侯亭波，等.电测法应用于材料力学实验中的教学实践[J].教育教学论坛，2018 （48）：115-116.

[9] 范钦珊，殷雅俊，唐靖林.材料力学[M].3版.北京：清华大学出版社，2014： 24.