稀疏约束的L21增量式非负矩阵分解研究

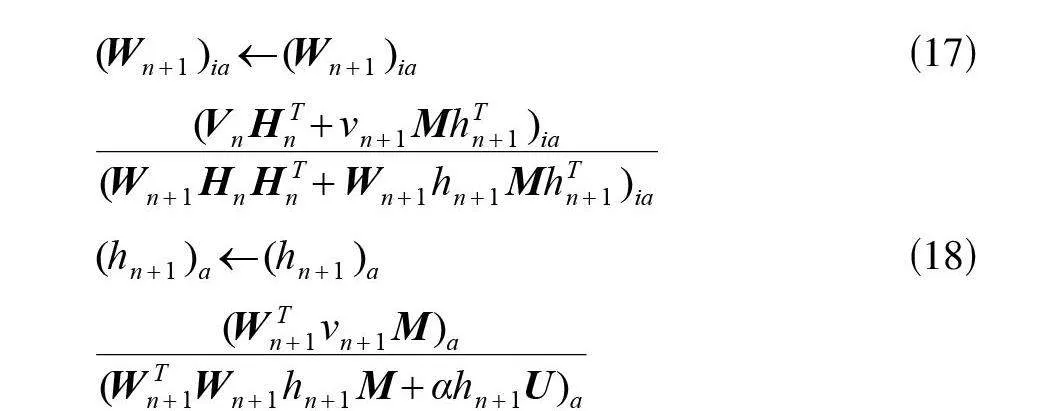
摘 要：针对新增数据增大而引起的运算效率增大的现象，提出了一种稀疏约束的增量式非负矩阵分解改进算法，该算法是在加入稀疏条件的情况下对增量数据使用L21范数。首先对初始数据进行经典非负矩阵分解，其次再利用其分解结果参与增量数据的运算，使目标函数在分解计算中具有较好的收敛效果和分解后数据有较好的稀疏度。实验部分，主要是将该算法与增量式非负矩阵分解、稀疏约束的增量式非负矩阵分解、经典非负矩阵分解算法进行了对比，得出在分解后数据的稀疏度和收敛快慢方面该算法均优于其他3个算法。

关键词： 非负矩阵分解 增量式学习 图像识别 稀疏约束 L21范数

中图分类号：TP391.41

Research onfRobustL21Incremental Non-nNegative Matrix Factorization with Sparseity Constraints

YANG Liangdong1ZHAOYanjie1 PANZhenghong 2*

1.Basic Teaching Department， Lanz Zhou Resources &Environment Voc-Tech University，Lanzhou ，GansSu Province， 730021 China;2.School of Public Health， GansSu University of cChinese Medicine ， Lanzhou，GanSsu Province， 730022 China

Abstract：In order tTo solve the phenomenon of the increasing operation efficiency caused by increasing new data， a sparse constraintn improved algorithm of incremental non-negative matrix factorizationdecompositionwith sparsityconstraints improvement algorithm is proposed， and Tthe algorithm isusestheinglL21 norm for incremental data in the case ofwith the addition a sparse conditions. Firstly， theclassical non-negative matrix factorizationdecomposition is performed on the initial data， and then its factorizationthe decomposition results are used to participate in the operation of the incremental data， so that the objective function has a better convergence effect in the decompositioncalculationof factorization and a better sparsity of thedecomposed data after factorizationhas a better sparsity. In the experimental part， the proposed algorithm is compared with incremental non-negative matrix factorization，sparse constraint incremental non-negative matrix factorizationwith sparsity constraints and classical non-negative matrix factorizationalgorithms， and it is concluded that the proposed algorithm is superior tobetter than the other three algorithms in terms of the sparsity and convergence speed of the decomposed dataafter factorization.

KeyWords：Non-negative matrix factorization; Incremental learning; Image recognition; Sparseity constraint; L21 norm

近年来智慧校园建设是一个重点工作，在校园安全方面图像识别技术是其中一项主要分支，而处理图像数据最为常见的一种方法是高维特征向量（矩阵数据）低维，有效避免了维度灾难[1]。为了达到这个目的，通常将矩阵进行分解，而矩阵分解最为常见的方法有主成分分析[2]、矩阵分解[3] 、判别分析[4]等。但是这些方法所得到的结果中会出现负值，可解释性不充分。因此1999年经典非负矩阵分解（Non-negative matrix factorization，NMF）算法在《Nature》杂志上由LEE D[5]和LEE D D[6]首次被提出，该算法的独特之处是添加了非负限制，不仅保证了分解结果的可解释性，还使分解后的数据具有较好的局部表达。有学者在此基础上又提出了一些改进算法[7-9]，并应用在图像识别、半监督学习、聚类等领域[10-13]。Bucak S S 等人[8]提出了增量式非负矩阵分解（Incremental non-negative matrix factorization，INMF），是利用前一步的分解结果参与后续运算，避免了重复运算。王万良等人[9]在此基础上对该算法进行了更新使算法更有时效性，提出了稀疏约束的非负矩阵分解增量式学习（Incremental non-negative matrix factorization with sparseconstraints，INMFSC）算法。

本文在对系数矩阵施加了稀疏约束的情况下，对增量数据的分解部分用L2，1范数来度量，从而提出了稀疏约束的L21增量式非负矩阵分解（Robust incremental non-negative matrix factorization with sparse constraints， RINMFSC）。

1 经典非负矩阵分解

对于初始样本 ，其中 为一个样本，n为初始样本的个数，则经典非负矩阵 的分解可表示如下：

（1）

式（1）中： 为基本矩阵，

为系数矩阵， 为基本矩阵的列数。当 时，就实现了对初始样本 的降维。

非负矩阵分解（NMF）算法[5-6]采用F范数来度量 与 的逼近程度，其优化问题可表示为如下：

min （2）

s .t.

由于目标函数 对 和 来说都是凸函数，因此在求解问题（1）时可采用梯度下降法分别对其进行交替更新。其更新公式如下所示：

（3）

（4）

其中，

。

2 RINMFSC算法

对给定的 个初始样本 ， 当有新增样本 加入时，

。为了对新增后的样本 进行稀疏约束的经典非负矩阵分解，可建立如下优化问题：

min （5）

s.t.

其中 和 分别是对初始样本 分解得到的基本矩阵和系数矩阵，而 和 分别是对新增样本 后的样本 分解得到的基本矩阵和系数矩阵 的最后一列， 为分解后基本矩阵的列数， 是稀疏限制项。 是矩阵的 范数[14]，其定义如下：

（6）

这里

，

是一个对角矩阵，并且

（7）

在优化问题（4）中， 新增样本的表达能力会随着初始样本的增加逐渐减弱。 因此当初始样本 足够大时， 并不会因新样本的增加而产生太大变化。因此根据以上假设，优化问题（5）可近似为：

min ; （8）

s.t.

式（8）中：

是基本矩阵， 是当初始样本为 时由问题（1）计算得出，因此最终所求解的系数矩阵为 ，可得问题（8）对新增一个样本后的数据矩阵 就近似做了分解。

为了求解问题（8），可将问题（8）的目标函数改为矩阵迹的形式如下：

（9）

其中 ，其元素分别为：

（10）

而式（9）中的 和 都是常数，其形式为：

（11）

（12）

式（12）中： 是很小的一个正数，这样处理是为了避免分母为0的情形。

因此， 可将优化问题（8）等价为：

min

s.t. （13）

为了求解带约束的优化问题（13）对约束条件 引入拉格朗日乘子 ， ，构造拉格朗日函数为：

（14）

分别对上式（14）中 和 求偏导，并令其等于零。 即

（15）

（16）

对（14）和（15）式两边分别乘以 和 ，利用KKT条件： ， ，可得如下的迭代法则：

（17）

（18）

根据式（17）、式（18）交替迭代得到当新增样本加入后最终所得系数矩阵增量部分 和新的 ，从而得到 。

3 实验结果及其结论

3.1 数据描述及其参数设置

（1）图1（a）中给出了USPS手写数字识别库[15]中部分样本的照片数据， 该数据集共有500张分辨率为 像素的照片组成。在每个数字中我们随机选择20张照片共有200张照片进行数值实验。

（2）图1（b）中给出了YALE人脸数据集[16]中部分样本的照片数据， 该数据库包含15人共165张分辨率为 像素的人脸照片数据。每类取6张共90张照片数据作为初始数据， 剩余75张照片作为新增数据进行实验。

在每次运算中使用随机初值对NMF[6]，INMF[8]，INMFSC[9]和RINMFSC进行实验， 如果 ≥ 时， 算法终止。

本文（RINMFSC）中有两个主要参数： 稀疏约束的参数 和基本矩阵的列数r。 通过对比多次实验， 在USPS手写数字识别库中稀疏约束的参数 ，设置基向量个数r为49。 在YALE人脸数据库中稀疏约束的参数 ， 设置基向量个数r 为36。

3.2 收敛效果对比

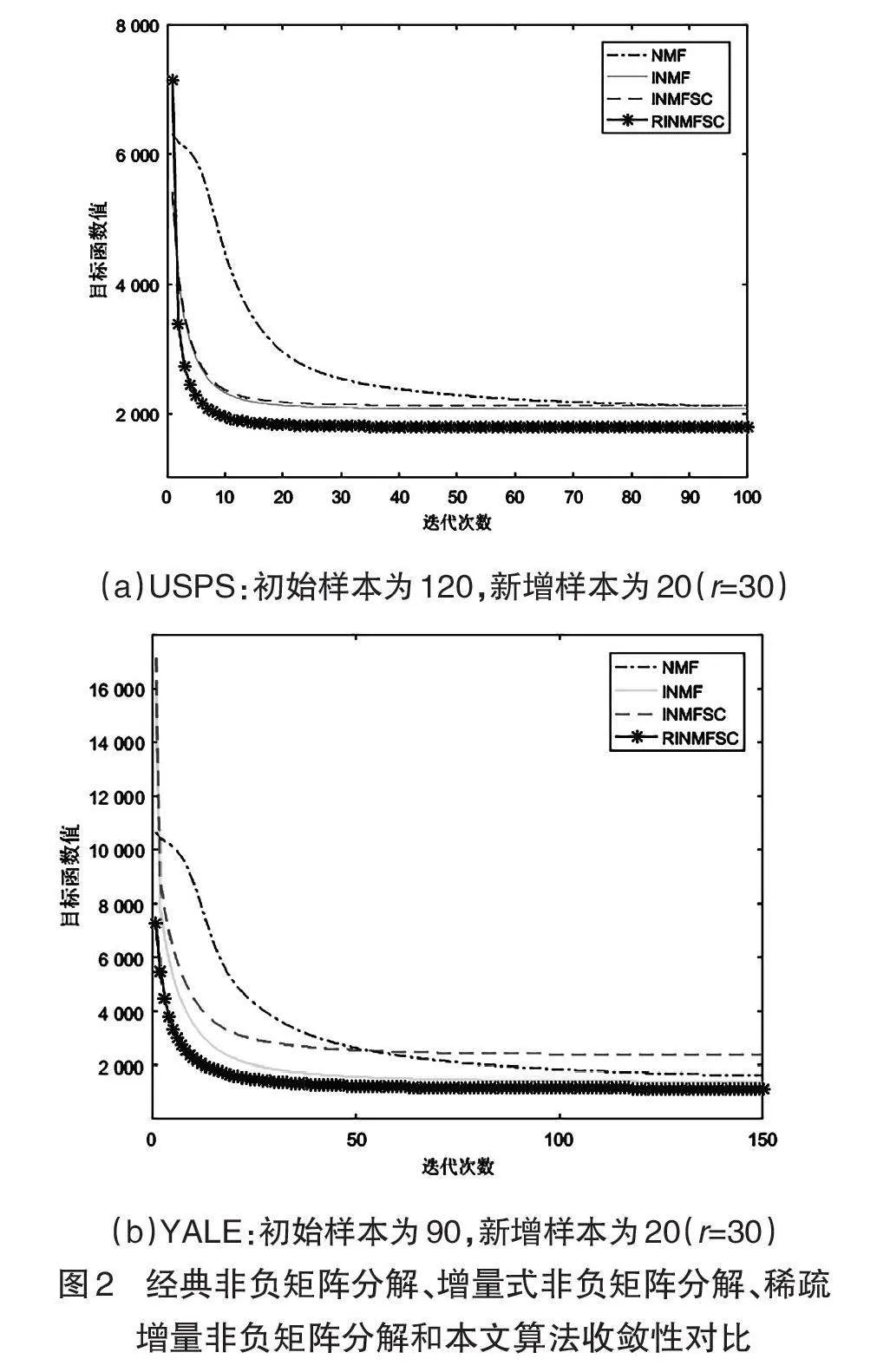
在YALE人脸数据库和USPS手写数字识别库上比较NMF[6]、INMF[8]、INMFSC[9]和本文算法的收敛效果情况如图2所示。

可得本文提出的算法的收敛效果均强于其他3个算法， 随着迭代次数的增加，本文算法目标函数值下降的最快，收敛效果较好，最先达到平衡，提高了运算效率。

3.3 稀疏限制的度量

首先定义稀疏函数为：

（19）

式（19）中：n为向量 的维数， 和 分别为向量 的1范数和2范数[16]。

式（19）作为稀疏度计算标准， 得到了本文算法和其他三个算法分解后的基本矩阵 的的基图像和它们的稀疏度如图3、图4所示。

由图3、图4可知，NMF算法的基图像最接近原图像，但是它的稀疏度较差， 存储率低，RINMFSC算法能得到更稀疏的基图像，图像的局部表达最佳。

4 结论

本文提出了一种增量式非负矩阵分解新的改进算法，并在YALE人脸数据和USPS 手写数据库上对该算法进行了验证， 结果显示与其他算法相比该算法仍然保持较好的收敛速度， 不仅减少了计算时间， 而且得到了更为稀疏的基图像，具有较强的局部表达能力。 但是， 该算法的不足之处是迭代初值和稀疏参数的选取， 目前没有一个统一的标准。

参考文献

[1] PARDALOS PM. Approximate dynamic programming：solvingthe curses of dimensionality[M]. Wiley， 2009：68-71.

[2] SHI W Y，GUO Y F，XUE X Y.A kernel principal component analysis algorithm for solving large scale data sets problem[J].Journal of Software，2009， 8（20）： 2153-2159 （in Chinese）.

[3] GOLUB G H， REINSCH C. Singular Value Decomposition and Least Squares Solutions[M]. Springer Berlin Heidelberg， 1971：403-420.

[4] XIAOHENG TAN， LU DENG.Optimized regularized linear discriminant analysis for feature extraction in face recognition[J]. Evolutionary Intelligence，2019（12）1：73-82

[5] LEE D. Learning the parts of objects with non-negative matrix factorization[J]. Nature， 1999， 401（6755）：788.

[6] LEE D D. Algorithms for non-negative matrix factorization[J]. Advances in Neural Information Processing Systems， 2001， 13（6）：556--562.

[7] 蔡竞，张嘉琪，钱康. 改进增量式非负矩阵分解算法及其在人脸识别中的应用[J]. 信息通信，2016（7）：4-7，8.

[8] BUCAK S S， GUNSEL B. Incremental subspace learning via non-negative matrix factorization[J]. Pattern Recognition， 2009， 42（5）：788-797.

[9] 王万良，蔡竞.稀疏约束下非负矩阵分解的增量学习算法[J].计算机科学， 2014， 41（8）：241-244.

[10] 李向利，梅建平，莫元健.基于超图正则NMF的自适应半监督多视图聚类[J/OL].广西师范大学学报（自然科学版）：1-16[2024-04-25].https：//doi.org/10.16088/j.issn.1001-6600.2023110202.

[11] 陈善学，许少华.基于图拉普拉斯正则化的柯西非负矩阵分解高光谱解混[J/OL].激光与光电子学进展：1-16[2024-04-25].http：//kns.cnki.net/kcms/detail/31.1690.tn.20231214.0028.022.html.

[12] 刘敬，李康欣，张悠，等.多图正则多核非负矩阵分解高光谱图像解混[J].光学精密工程，2022，30（14）：1657-1668.

[13] 董秋宇.非负矩阵分解及其在遮挡人脸识别中的应用[D].西安：西安电子科技大学，2022.

[14] KONG D， HUANG H. Robust nonnegative matrix factorization using L21-norm[J] AcmConference on Information & Knowledge Management ， 2011：673-682.

[15] 杨亮东.基于L_（2.1）稀疏限制的增量式非负矩阵分解[D]. 乌鲁木齐：新疆大学，2019.

[16] 杨亮东，杨志霞.稀疏限制的增量式鲁棒非负矩阵分解及其应用[J].计算机应用，2019，39（5）：1275-1281.