复合材料圆柱壳体的层间断裂韧性分析

摘 要：针对复合材料圆筒的层间性能分析，通过双悬臂梁试验（Double Cantilever Beam，DCB），得到了复合材料I型层间开裂与载荷对应关系，并根据GIC计算公式得到了材料I型断裂韧性。通过三点（+端部开口？？）弯曲？？试验（End-Notched Flexure， ENF），计算了材料II型断裂韧性。建立了有限元模型，将I型断裂韧性、II型断裂韧性代入材料本构模型参数，对该结构层间性能设计与评估提出理论指导。

关键词：复合材料层间强度 断裂韧性 双悬臂梁试验 三点弯曲试验

中图分类号：TB33

Analysis of the Interlaminar Fracture Toughness of Composite Cylindrical Shells

JIA Liwei 1， 2 LI Wusheng1

1. ResearchInstitute of Physical and Chemical Engineering of Nuclear Industry， Tianjin， 300180 China; 2.Harbin Institute of Technology， Harbin， Heilongjiang Province，150006China

Abstract：The interlaminar performance of composite cylindersis analyzed. Through the Double Cantilever Beam （DCB） test， the correspondence between the Type I interlaminar cracking and load ofthe composite material is obtained， and itsType-I fracture toughness is obtained according to the G1C calculation formula. Through the three-point End-Notched Flexure （ENF） test， the Type-II fracture toughness ofthe materialis calculated. A finite element model is established， and Type-I fracture toughness and Type-II fracture toughness are substituted into the constitutive model parameters ofthe material， which provides theoretical guidance for the design and evaluation of the interlaminar performance of the structure.

Key Words： Composite material; Interlaminar strength; Fracture toughness; Double cantilever beam test; Three-point end-notched flexure test

采用纤维缠绕工艺成型的复合材料圆柱壳由于其环向的高比强度，在压力容器、压力管道、玻璃钢等领域得到了广泛发展。在高速转子部件中复合材料长期处于高应力状态，此时材料结构内部微小的损伤都可能导致整个结构瞬间破坏。损伤在空间上分为层间损伤和层内损伤两种类型[1-2]，本文重点针对层间损伤开展研究。研究层间分层问题的核心在于计算裂纹尖端的物理场。为了计算更加精细的界面裂纹尖端物理场，数值计算方法逐渐兴起，包括边界元法、J积分法、M积分法、界面单元法、虚拟闭合裂纹技术（Virtual Crack Closure Technique，VCCT）和内聚力模型法（Cohesive Zone Model，CZM），其中VCCT和CZM是最为常用[3]。WEI R F[4]采用VCCT方法建立了I型、II型和III型层间开裂的有限元模型并开展了水下复合材料圆柱壳受压发生层间破坏的结果。

本文针对某专用复合材料圆筒的层间抵抗分层或裂纹扩展能力开展研究。通过双悬臂梁（Double Cantilever Beam，DCB）试验并根据G1C计算公式得到了材料的I型断裂韧性。通过三点弯曲试验（End-Notched Flexure， ENF）并计算了材料的II型断裂韧性。建立了复合材料结构有限元模型，把试验获取的I型断裂韧性、II型断裂韧性代入材料本构模型参数，对该结构的层间性能设计与评估提出理论基础。

1 复合材料I型层间断裂韧性研究

纤维与基体间的界面脱粘和分层失效是专用设备复合材料转筒常见的损伤形式之一，本文为开展专用设备复合材料抵抗分层或裂纹扩展能力研究，首先开展了复合材料层间断裂韧性评价。材料裂纹的分层模式一般分为I型、II型、III型以及这3种的混合形式[5，6]，在复合材料转筒实际工作过程中受到的载荷更为复杂。在以上3种裂纹模式中，I型裂纹扩展形式的测试相对较成熟，在实际应用中更广泛，本文针对I型裂纹开展评价。

GIC即为Ⅰ型层间断裂韧性，也称临界能量释放率，它是指在Ⅰ型张开载荷下，单向纤维增强聚合物基复合材料层合板对分层裂纹起始及扩展的阻抗，单位J/m2。复合材料I型层间断裂韧性测试的试样形式通常有双悬臂梁（DCB）试样和楔形双悬臂梁试样两种，本文将采用DCB试样。目前关于Ⅰ型层间断裂韧性的测试标准主要包括美标ASTM D5528-13，国标GB-T 28891—2012/ISO 15024：2001与航标HB 7402-96，本文选择国标开展评价研究。为与转筒复合材料实际情况接近，采用缠绕工艺制备复合材料平板试样，并在厚度方向居中位置铺覆薄膜预埋裂纹。

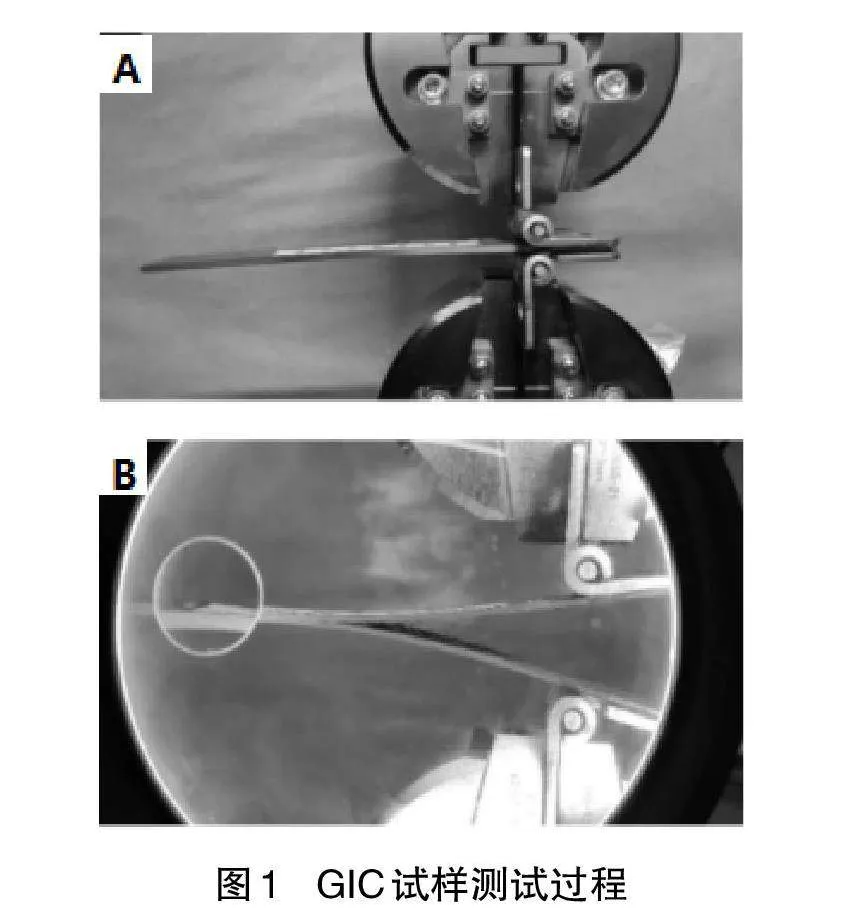
按照国标与美标中载荷加载方式，开展测试，详见图1。图中A为试样加载实际情况，在试样预制裂纹区域固定铰链用于试样夹持，拉伸铰链转动轴中心均与夹持线对中，试样保持水平，试样表面粘贴刻度尺以便裂纹长度读取。图中B为试样加载中试样张开、裂纹扩展与裂纹长度读取过程。测试过程经历两次加载，第一次加载后在预制裂纹前端产生自然引发的裂纹尖端，第二次加载则为获取载荷、行程与裂纹长度数据，从而计算得到GIC值。

本文选择的数据处理方式为国标与美标中通用的修正梁理论，同时引入大变形系数。

（1）

（2）

（3）

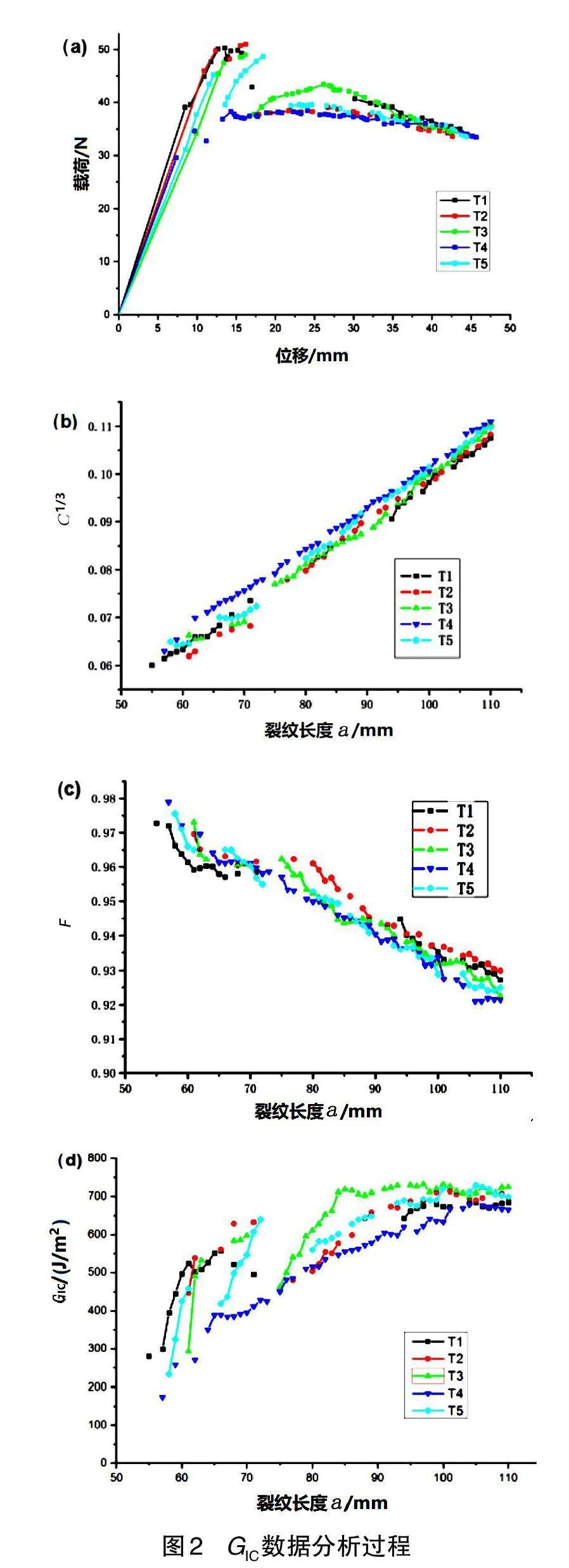
式（1）、式（2）、式（3）中：P为载荷；δ为位移；a为裂纹长度；b为试样的宽度；F为大变形系数；t为铰链转动轴中心距试样上1/4厚度位置的垂直距离；C为柔度；∆为C1/3与a函数关系中的横坐标截距。GIC数据分析过程见图2，图中a为载荷-位移关系图，在裂纹扩展初始阶段，载荷-位移呈线性关系，达到最大值后陡降，之后在一定范围内呈起伏波动状，这是由于裂纹扩展过程伴随着旧纤维断裂以及新纤维受到载荷；图b为柔度立方根-裂纹长度关系图，拟合曲线后，曲线与横坐标交点即为∆，图c为大变形系数-裂纹长度关系图，图d为GIC-裂纹长度关系图，即分层阻力曲线。

2 复合材料II型层间断裂韧性的测试与分析

2.1 ENF的数值模拟与分析

本部分将通过对比数值模拟分析的结果与试验结果来达到两个目的：一是确定Arc-ENF试样在三点弯曲试验中所记录的裂纹长度值的修正；二是确定Arc-ENF试样的II型层间断裂韧性GIIC。而试样的复合材料参数与DCB试验的相同。层间界面模型仍然采用双线性内聚力模型，而关于GIIC公式中的修正项的参数，取=2.9°，fk=0.25，则需要根据试验数据来确定。

2.2 复合材料II型层间断裂韧性测试

目前关于复合材料的II型层间断裂韧性的测试，试样形式一般为单向纤维增强复合材料的末端切口试样，而试验形式包括三点弯试验（End-Notched Flexure， ENF）、四点弯试验（Four Point Bend ENF， 4ENF）和端部载荷分离试验（End Loaded Split， ELS）等。本文也采用ENF试验对Arc-ENF试样进行测试。

对于ENF试验装置，如图3所示，其支撑点与加载点处的细圆棒的直径为3 mm，两个支撑的间距为40 mm；试验过程中加载速度为4 μm/s，主要是为了保证裂纹准静态扩展。为了判断裂纹尖端位置在试验过程中利用光学应力仪对试样的x-y平面进行拍照，经过后期数据处理可以得到加载过程中各个时刻的试样变形情况，即x-y平面应变云图，如图3所示，而裂纹尖端位置根据x方向应变为5%的位置确定，即图中的A点。最终记录ENF试验过程中加载点的位移值，载荷值和相对应的裂纹长度值。

3 结论

（1）通过双悬臂梁（DCB）试验，得到了复合材料I型层间开裂与载荷的对应关系，并根据G1C计算公式得到了材料的1型断裂韧性。

（2）设计了ENF试验装置，通过三点弯曲（ENF）试验，测试了II型层间裂纹扩展长度与载荷的对应关系，据此计算了材料的II型断裂韧性。

（3）建立了复合材料结构有限元模型，在材料本构模型参数中引入前期试验获取的I型断裂韧性、II型断裂韧性。

参考文献

[1] 熊健，李志斌，刘惠彬，等.航空航天轻质复合材料壳体结构研究进展[J].复合材料学报，2021，38（6）：1629-1650.

[2] 黄亿洲，王志瑾，刘格菲.碳纤维增强复合材料在航空航天领域的应用[J].西安航空学院学报，2021，39（5）：44-51.

[3] 付晨.纤维增强复合材料层合板分层损伤机理与预测方法研究[D].北京：北京交通大学，2022.

[4] WEI R F，SHEN K C，PAN G.A numerical study on the effect of delamination on composite cylindrical shells subjected to hydrostatic pressure[J]. Ocean Engineering， 2022（262）：112294.

[5] 张旭东，段青枫，曹东风，等.基于复合材料I型分层损伤机制的解耦内聚力方法[J/OL].复合材料学报：1-15[2024-05-10].https：//doi.org/10.13801/j.cnki.fhclxb.20240311.004.

[6] 王雅娜.复合材料Ⅱ型分层 ENF 试验数据处理方法对比分析[J].复合材料科学与工程，2022（7）：81-92.