基于径向基函数神经网络的无刷直流电机多机电故障处理方法
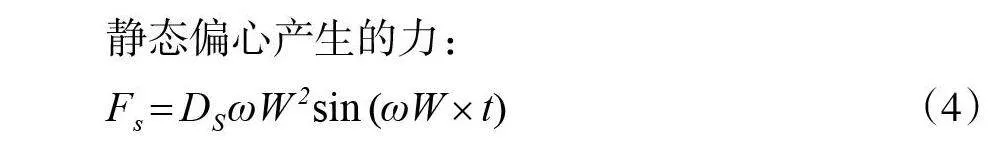



摘要:解决无刷直流电动机的故障检测和分类问题,提出了一种新的诊断方法,可用于定位定子间转、转子动力和静力不平衡等多种机电故障。结合无刷直流电动机电流信号、电机转矩和速度信息,利用小波包变换提取故障特征,并将其作为径向基函数神经网络的输入数据。通过粒子群优化算法和遗传算法对神经网络权值进行更新,提高了算法的效率和灵活性。最终,通过比较不同神经网络和优化方法的组合结果验证了该方法的有效性。
关键词:无刷直流电动机 小波包变换 神经网络 粒子群优化算法 遗传算法
Treatment Methods for the Multiple Electromechanical Faults of Brushless DC MotorsBased on the Radial Basis Function Neural Network
CHANG Yuyan
(Suzhou Vocational and Technical College, Suzhou,Anhui Province, 234001 China)
Abstract: In order to solve the problem of the fault detection and classification of brushless DC motors, this paper proposes a new diagnostic method that can be used to locate vcbf9e16901d7a0bcb89fba1521b02396arious electromechanical faults such as the inter-turn fault of thestator, and the dynamic and static imbalance of the rotor.Combined with the current signal, motor torque and speed information of the brushless DC motor, it extracts fault features by the wavelet packet transform and uses them as the input data of radial basis function neural networks. By the particle swarm optimization algorithm and genetic algorithm, it updates the weights of the neural network, which improves the efficiency and flexibility of algorithms. Finally,it verifies the effectiveness of the proposed method by comparing the combined results of different neural networks and optimization methods.
Key Words: Brushless DC motor; Wavelet packet transform; Neural network; Particle swarm optimization algorithm; Genetic algorithm
近年来,无刷直流电机因其较高效率将电能转化为机械能、结构简单、维护成本低、无刷设计的特点以及低摩擦设计而在各种应用中备受青睐。由于电子板故障,无刷直流电机可能会出现多种缺陷,包括定子、转子和磁性缺陷。这些缺陷可能带来重要问题,如降低无刷直流电机的性能、效率或系统的安全性,因此无刷直流电机的故障检测问题备受关注。主要解决方法包括基于系统建模[1]和基于信号的方法,基于系统建模的方法主要依赖于准确的模型和对系统不确定性的理解。此外,基于信号的方法则利用测量的关键信号[2-3]进行状态监测,无须精确的系统建模。针对无刷直流电机的故障检测,数据驱动的方法尤为重要,其中,人工智能技术备受关注。径向基函数神经网络是一种有效的技术,用于检测无刷直流电机的故障。此外,还有一些混合方法,结合信号处理和人工智能工具[4],例如神经网络、模糊系统[5]和支持向量机[6]。
综上所述,通过综合利用不同方法的特点可以更准确地检测和分类无刷直流电机中的故障[7]。之前的研究已经介绍了一些基于分组小波变换、支持向量机和径向基函数神经网络的轴承故障检测方法。对未来研究深度学习[8]和大数据技术的引入以及远程监测和诊断将是关键方向。与传统依赖于电流或振动信号的方法不同,电流信号与电机转矩和转速信号相结合,以提高故障分类的准确性。
1 无刷直流电机故障情况
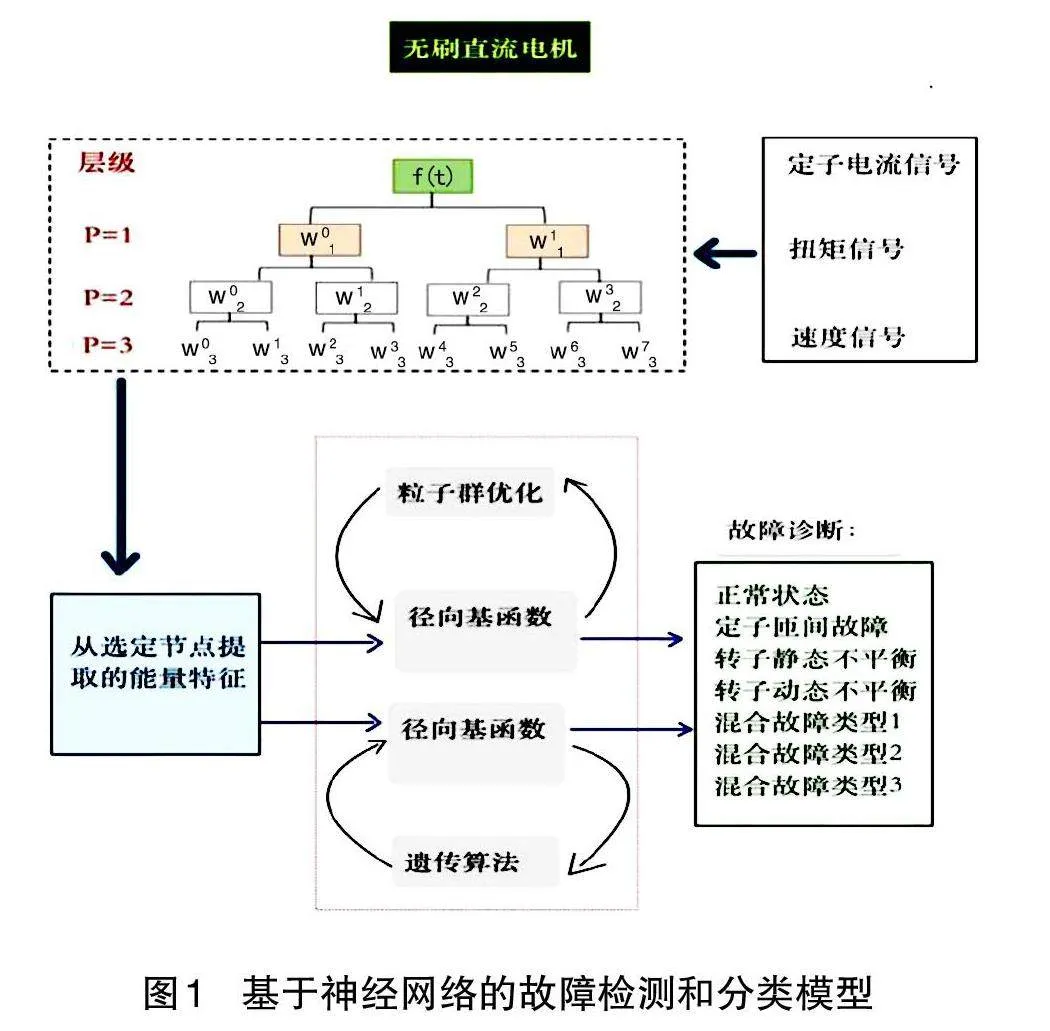
无刷直流电机的故障可分为七种类型,包括定子匝间故障、转子静态不平衡、转子动态不平衡、混合故障类型1(定子匝间故障和转子静态不平衡)、混合故障类型2(定子匝间故障和转子动态不平衡)、混合故障类型3(转子静态不平衡和转子动态不平衡),最后是混合故障类型4(同时发生定子匝间故障,转子静态不平衡和转子动态不平衡),下文将详细讲述和分析不同故障类型的实际机制。针对多种故障的实际情况,本文设计了故障诊断方法的基础模型。首先本模型先行测量了无刷直流电机的电流、扭矩和速度信号,并利用小波包变换提取与这些信号相关的特征。这些特征包括了无刷直流电机在两种操作模式下的能量:即无负载状态和有负载状态,这些将被作为输入供给径向基函数神经网络,神经网络的权重系数由粒子群优化算法和遗传算法作为优化算法来确定。模型的详细情况将在图1展示。
当要分析并排除无刷直流电机的故障时,首先需要了解其工作原理和运行特性,以下方程式和参数描述了BLDCM在不同工作条件下的运行特性,包括了电磁转矩、机械运动和负载扭矩等因素。
BLDCM的相间电压 (Va, Vb, Vc)由以下方程式给出。
V_ab=R(i_a-i_b )+L _a/dt+E_a-E_b
V_bc=R(i_b-i_c )+L _b/dt+E_b-E_c
V_ca=R(i_c-i_a )+L_c/dt+E_c-E_a
其中,R为电极电阻,L为自感,E为电机的电动势。
定子匝间故障
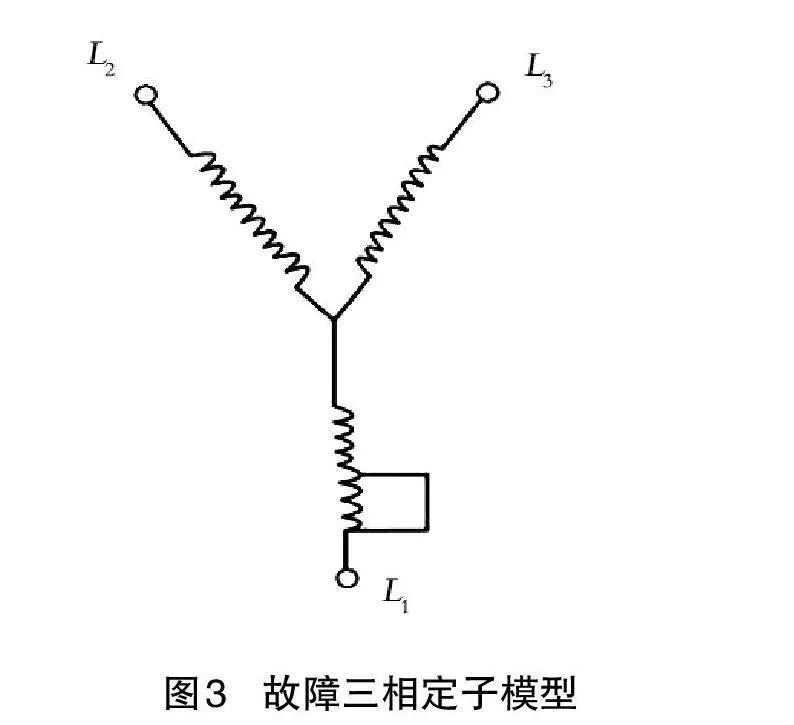
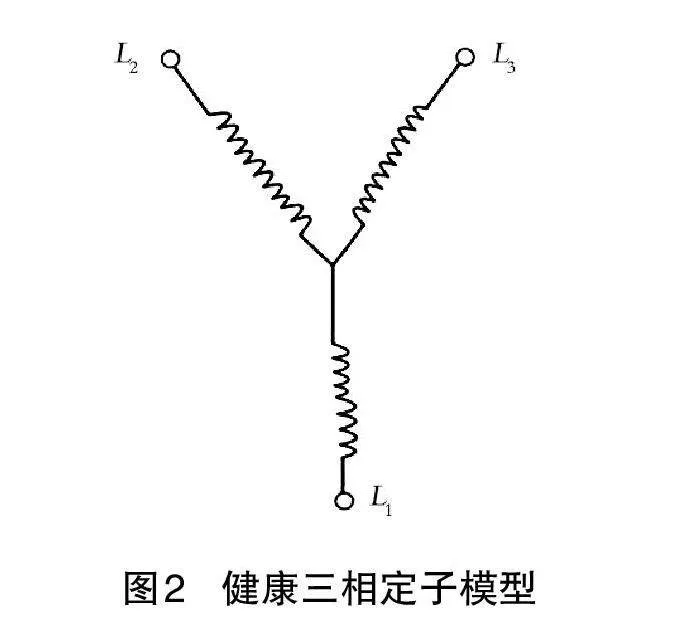
定子匝间故障是电机故障中比较常见的一种[9],但具体占比会因电机类型、使用环境等因素而异。一般来说,定子匝间故障在电机故障中的比例可能会在30%~50%之间。造成定子匝间故障的原因主要包括3个方面:一是绝缘老化或损坏,随着电机使用时间的增长,定子绝缘会逐渐老化,或者在运输、安装等过程中发生损坏,导致匝间故障;二是长期过载运行、频繁起停、电压不稳定等因素可能导致定子绕组承受过大的电气应力,增加了匝间故障的风险;三是灰尘、水分、异物等进入电机内部,或碰撞、振动等外部因素导致定子绕组的外部物理损伤。三相定子中的短匝间故障模型可以用电路形式来表示,分别是健康三相定子和故障三相定子,通过图2、图3展示详细的电路情况。
在健康的情况下,三相定子绕组之间是均匀连接的,相互之间没有任何短路。
在定子匝间故障三相定子电路模型中(假设故障发生在L1线圈内),出现了一条额外的电路路径,导致电流异常增大,可能引发电机故障。
转子静态和动态的不平衡故障
在机械系统中,转子的不平衡可以导致静态和动态偏心。理想情况下,转子的旋转轴与定子的对称轴完全匹配,并且空气间隙在整个转子周围都是均匀的。但实际上,由于各种因素,如材料不均匀、安装问题等,转子可能会偏离理想状态,产生偏心。
静态偏心发生时,最小径向空气间隙的位置保持不变,并且转子的中心与转子的旋转中心不重合。这可能是由于定子对称轴和转子对称轴之间的分离导致的。静态偏心通常由于电流椭圆形状或转子位置错误等原因引起[10]。动态偏心则是指转子中心不在转子的旋转中心上,并且径向空气间隙发生旋转。这可能是由于轴弯曲、机械共振或轴承磨损等原因导致的。静态偏心和动态偏心都可以使用以下公式进行建模。
静态偏心产生的力:
公式:F_s=D_S ωW^2 sin〖(ωW×t)〗
这个公式描述了静态偏心产生的力,其中:
D_S是静态扰动系数,表示转子静态偏心的程度。这个系数衡量了偏心对转子运动的影响。
ωW是转子的角速度,表示转子的旋转速度。
t是时间。
sin(ωW×t) 是一个正弦函数,描述了随时间变化的力的大小和方向。
静态偏心产生的力与静态扰动系数、转子的角速度以及时间有关。当时间变化时,产生的力也会随之变化。
动态偏心产生的力:
公式:F_d=D_d ωW^2 sin〖(ωW×t)〗
这个公式描述了动态偏心产生的力,其中:
D_d是动态扰动系数,表示转子动态偏心的程度。与静态扰动系数类似,这个系数也衡量了偏心对转子运动的影响。
其他符号的含义与静态偏心的公式相同。
动态偏心产生的力也与动态扰动系数、转子的角速度以及时间有关,与静态偏心的公式类似,力的大小和方向随时间变化而变化。通过以上公式和模型可以更好地理解转子的静态和动态不平衡对机械系统的影响,以及它们如何通过无刷直流电机信号中的谐波体现出来。
混合类型故障
针对定子匝间故障和转子静态或动态不平衡的组合混合类型故障[11],这种混合类型故障可能会导致电机性能整体下降,同时增加机械部件的损坏风险。定子匝间故障[12]可能导致电机温升异常,进而加剧转子静态不平衡和动态不平衡的影响,造成机械振动加剧,加速电机寿命的缩短。为了有效诊断和预防这种混合类型故障,可能还需要结合振动分析、电流分析、绝缘测试等多种手段进行全面检测,预防措施包括定期维护检查、合理的负载运行、注意电机安装平衡等。
2无刷直流电机故障检测和分类方法
本文通过设定的基于神经网络的无刷直流电机故障检测和分类方法模型进行步骤逐一分析和推演,可参考图1。
通过获取定子电流信号,扭矩信号和速度信号数据后,使用小波包变换在4种不同的负载条件下进行分析,包括无负载(No load,NL)、半负载(Half load,HL)、全负载(Full load,FL)和减负载(Decreased load,DL),其中,本文将分解等级定为13,并针对每种信号在4种不同负载条件下生成了213个节点,对每种信号,选取了5个节点进行特征提取。这些节点的频率带包含故障频率,因此被本实验认定为故障特征的合适候选。然后将进行特征计算,对于每个节点计算其能量,公式表达为:
其中,k是节点的索引。最后将4种不同负载条件下以及8种不同故障条件下的信号的这些节点能量作为特征,输入神经网络中进行故障分类。
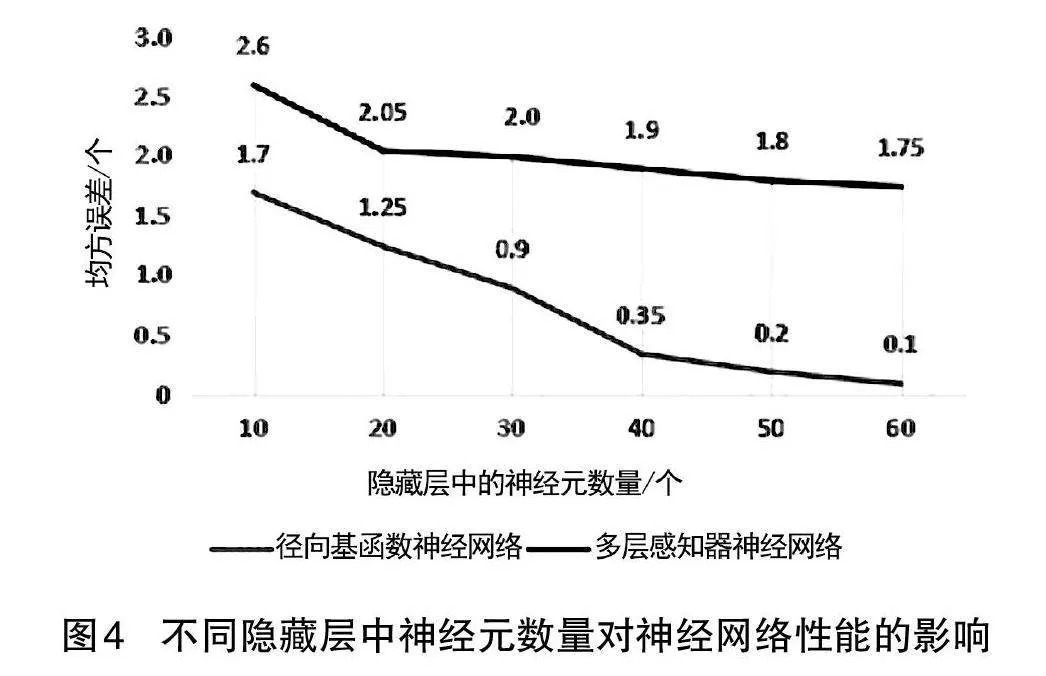
小波包变换系数的能量将在4种不同负载条件和7种不同故障条件下作为径向基函数神经网络的输入,神经网络训练算法将首先设置输入层权重到隐藏层,然后设置隐藏层权重到输出层。特征提取数据被用作神经网络分类器的训练和测试数据,即每种电机条件和几个负载水平各有15个数据集。总的来说,共有480个数据集,其中60%用于神经网络训练,40%用于神经网络测试。对于每种无刷直流电机条件,预计用1500个数据集来训练神经网络。评估了径向基函数和多层感知器神经网络以确定最佳的故障诊断性能。每个神经网络在输入层有3个神经元,在输出层有1个神经元,在隐藏层有不同数量的神经元。如图4所示,当隐藏层中的节点数为60时,径向基函数神经网络提供了最佳性能,达到了均方误差(Mean Square error,MSE) 为0.0930。此外,多层感知器神经网络提供均方误差(MSE)为1.6571,需要60个隐藏层节点。因此,对于数据训练步骤,径向基函数神经网络获得了更好的性能。
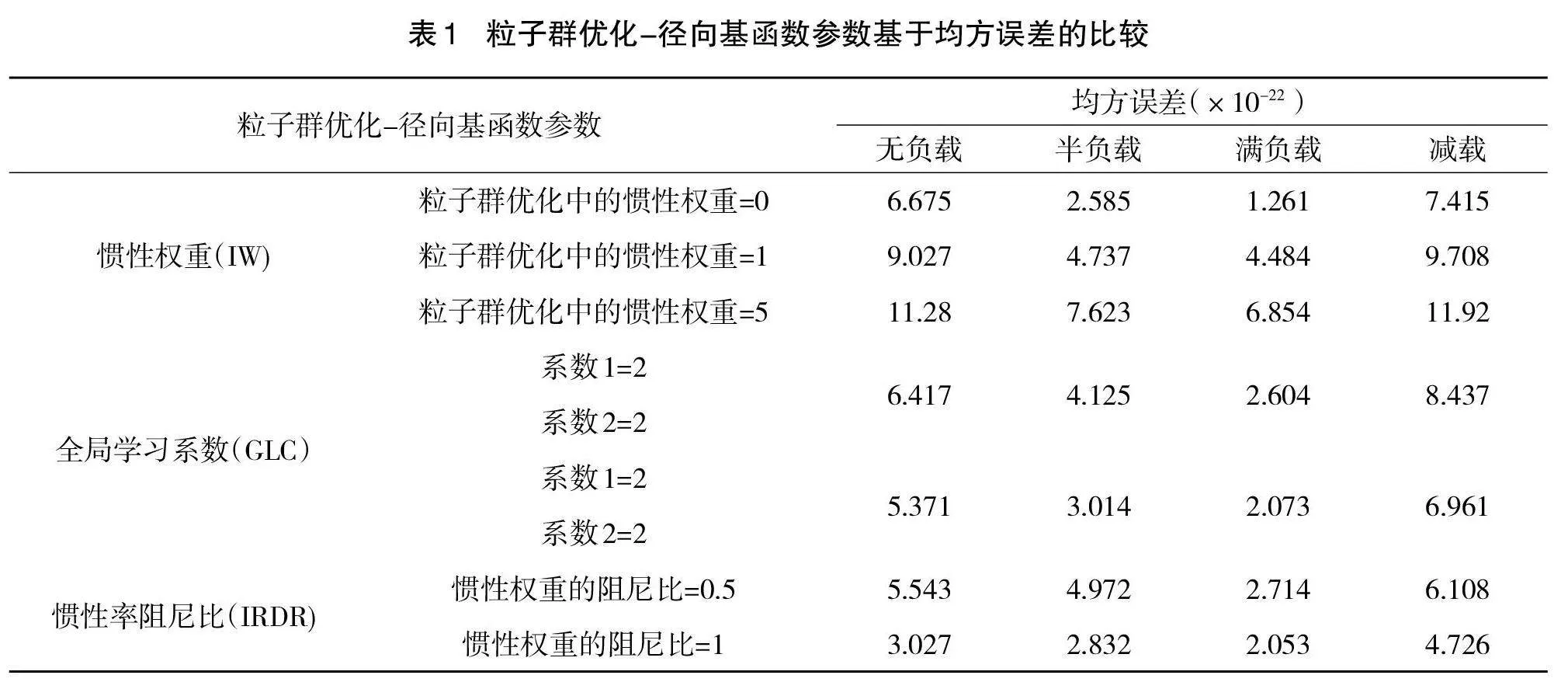
为了实现神经网络的最佳分类性能,还需要获得最适合优化算法(即粒子群优化和遗传算法)的参数,以及为了说明对粒子群优化算法的惯性权重、个人和全局学习系数以及惯性率阻尼比的影响,给出了4种不同负载条件的结果,如表1所示。在该表中,为简化起见,惯性权重、全局学习系数和惯性率阻尼比分别命名为IW、GLC和IRDR。在该表中,给出了不同粒子群优化参数值对应的结果MSE。通过考虑上述因素,选择了惯性权重、个人和全局学习系数和惯性率阻尼比分别为0、1.5、2和1。
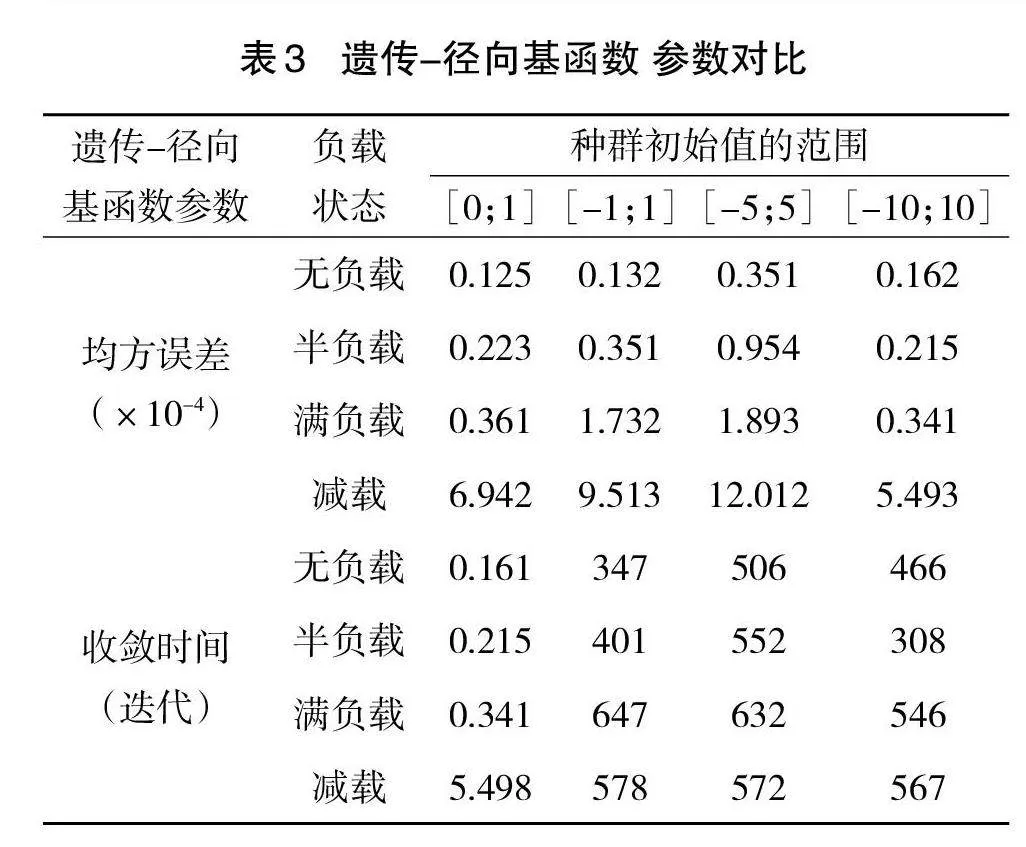
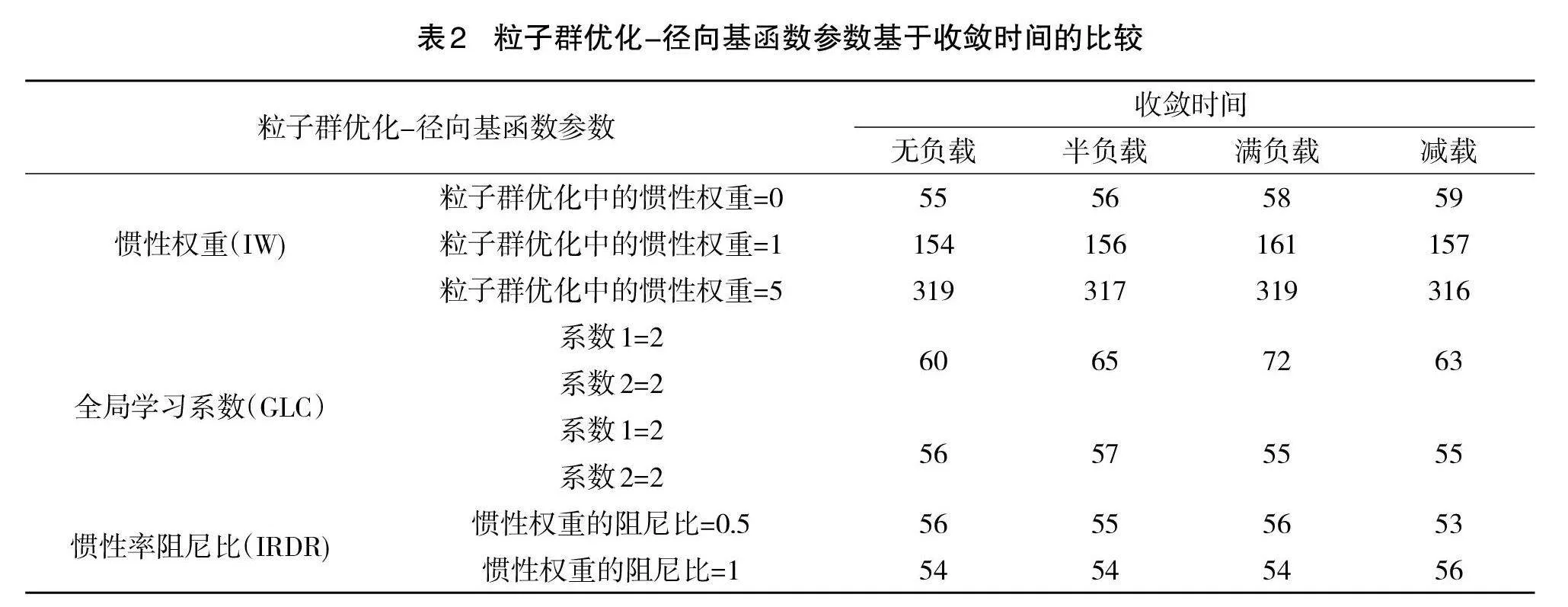
根据表2,在遗传算法中选择的初始种群范围参数的值[0;1]导致了最适当的性能。为了说明惯性权重、个人和全局学习系数以及惯性率阻尼比对粒子群优化算法的影响,基于收敛时间给出了4种不同负载条件的结果,如表2所示。
根据表3,在遗传算法中选择的初始种群范围参数的值[0:1]导致了最适当的性能。正如这些表格所示,RBF神经网络与粒子群优化算法的组合实现了最佳性能。
3故障诊断方法性能验证
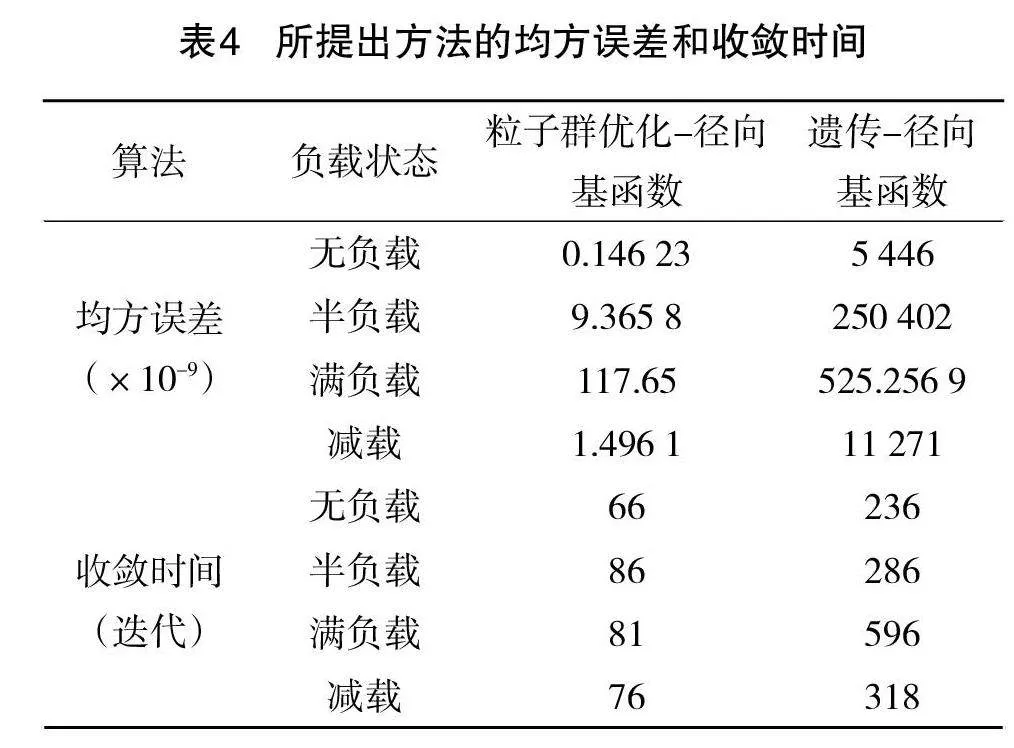
为展示验证阶段的诊断算法结果,考虑无刷直流电机的故障条件,选择了以下测试情景,即静态不平衡从时间t=2开始。故障诊断的结果如表4所示,对比粒子群优化-径向基函数和遗传算法-径向基函数方法。正如表4所示,所研究的网络在不同负载水平下都达到了可接受的均方误差(MSE)和收敛时间。然而,粒子群优化方法获得了更好的性能值,在更短的收敛时间内提供了更准确的结果。
在本文中,径向基函数神经网络可以对7种不同的无刷直流电机故障进行分类。在健康状态下,径向基函数输出显示数字1,而如果显示数字2、3、4、5、6、7和8,则分别对应表示无刷直流电机具有转子静态不平衡、定子匝间故障、转子动态不平衡、混合故障类型1、混合故障类型2、混合故障类型3和混合故障类型4,并在最后验证了所提出算法的有效性。
4结语
针对不同无刷直流电机条件(定子匝间故障、转子静态不平衡和转子动态不平衡)的多故障分类的故障诊断方法。通过使用电流信号、机电转矩和电机转速作为诊断媒介,并利用小波包变换提取能量特征,展示该方法能够有效地隔离各种故障。提取的特征用作基于神经网络的分类器的输入。粒子群优化和遗传算法被推荐为优化方法,用于更新神经网络的权重。研究结果表明,径向基函数-粒子群优化方法具有更短的收敛时间,同时能够获得更准确的结果。进行了进一步的测试以评估该方法,结果证实了设计的算法在可接受的收敛时间内能够达到所需的分类准确性。因此,提出的故障诊断特征和神经网络与小波包变换方法的组合能够有效地对不同操作条件下的无刷直流电机故障进行多重诊断。为了增强该方法的性能,未来的研究可以考虑使用不同负载模式下的无刷直流电机,并提出适用于各种负载条件的故障检测和分类方法。
参考文献
MEKKI A E,SAAD K B.Diagnosis based on a sliding mode observer for an inter-turn short circuit fault in brushless dc motors[J].Revue Roumaine des Sciences Techniques-Electrotechnique et Energétique,2018,63(4):391-396
GUEZMIL A,BERRIRI H,PUSCA R,et al.Detecting inter-turn short-circuit fault in induction machine using high-order sliding mode observer: simulation and experimental verification[J]. Journal of Control, Automation and Electrical Systems, 2017,28(4): 532-540.
LEE C Y,LE T A.Optimised approach of feature selection based on genetic and binary state transition algorithm in the classification of bearing fault in BLDC motor[J].IET Electric Power Applications,2020,14(13):2598-2608.
[4] 彭小玉,潘小东,申涵寒,等.基于正则模糊划分的模糊系统及其逼近性质[J].计算机科学,2024,51(2):79-86.
[5] RAY S,GANGULY B,DEY D.Identification and Classification of Stator Inter-Turn Faults in Induction Motor Using Wavelet Kernel Based Convolutional Neural Network[J].Electric Power
Components and Systems,2020,48(12-13):1421-1432.
[6] 王吉亮.无刷直流电机匝间短路故障的定位及定量评估研究[D].合肥:安徽大学,2022.
[7] 魏秀参,肖亮.新工科背景下深度学习理论实践一体化课程与教材建设改革[J].计算机教育,2024(4):135-143.
[8]SARDANA G, TURK N, DESWAL S.Detection of stator winding faults using finite element analysis (FEA) in bldc motors[J].International Refereed Journal of Reviews and Research,2018,6(2):50-58.
[9]RAJAGOPALAN S,ALLER J M,HABETLER T G,et al.Analytic-wavelet-ridge-based detection of dynamic eccentricity in brushless direct current (BLDC) motors functioning under dynamic operating conditions[J].IEEE Transactions on Industrial Electronics,2007,54(3):1410-1419.
[10] 何玉灵,王世云,孙凯,等.轴径向静态偏心故障下外转子永磁发电机电磁转矩特性分析[J].电机与控制学报,2024,28(1):12-25.
[11]董一汉,朱建光.基于神经网络的无刷直流电机故障诊断研究[J].电脑知识与技术,2021,17(30):111-113.
[12] 王立平,陈仁文.基于小波包分形的电力电子故障诊断方法[J].测控技术,2017,36(5):5-8.

