一种基于可拓学的中小型软件体系评价与优化实践

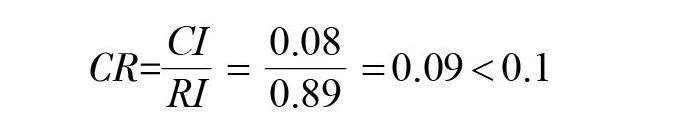
摘要：针对企业中小型软件模块体系在评价过程中对复杂的定性分析，缺少客观准确的评价，易造成中后期评审优化等阶段反复修改，影响企业开发成本、开发质量和经济效益。通过可拓学建立基元模型，利用Python中的numpy库辅助相关矩阵进行计算，利用层次分析法（Analytic Hierarchy Process，AHP） 对各个指标层和准则层进行评价，将复杂的定性分析转化为借助人工智能工具的定量计算。在指标层利用相关网模型聚焦该软件存在的主要问题，进行优化与改进，最终提升该软件模块体系质量，实现降本增效。

关键词：可拓学;层次分析法; 体系评价；人工智能；相关网

Practice of the Evaluationand Optimization of AaSmall -and Medium-SizedSoftware SystemEvaluationand Optimization PracticeBased on Extenics

YAN Jicheng1YOU Yue2

1．Changan Communication Technology Co.， Ltd.， Beijing ，101300 China；

2．CSSC Shanghai Marine Diesel Engine Research Institute，Shanghai ，201108 China

Abstract： In the evaluation process of the small-and medium-sized enterprise software module system in enterprises， there is a lack of the objective and accurate evaluation due toof complex qualitative analysis.This situation， which is easy to cause repeated modifications in the middle and later stages of review and optimization， affecting the development cost， development quality and economic benefits of enterprises.In this paper， the primitive model is established by extenics theory，Tthe numpy library in Ppython is used to assist the calculation of the correlation matrix for calculation.，and theAnalytic Hierarchy Process （AHP） is used toThe evaluateion is carried out according to each index layer and criterion layer through AHP analytic hierarchy process.， so as toTtransform complex qualitative analysis into quantitative calculations with the help of artificial intelligence tools.In the index layer， the correlation network model is used to focus on the main problems of the software and optimize and improve it， and.Ffinally improve the quality of the software module system is improved， so as to reduce the costs and increase the efficiency.

Key Words： Extenics; Aanalytic hierarchy processHP; System evaluation; Artificial intelligence; Correlation network

随着科技迅猛发展与推进，中小型软件更符合部分企业短周期获得高回报率等特点，且需求变化灵活。但针对初创企业，其软件模块体系评价，仍不够成熟，在评价过程中通常受到技术研发能力、经济条件以及其他因素的影响，缺少针对相关体系客观准确的评价体系和优化方法。目前，国内企业和学者对基于可拓学和层次分析法等方法对体系进行评价的方法，均开展了相关研究。例如：冷超等人[ ]基于模糊综合评价体系构建了软件的质量等级，王燕妮等人[ ]基于可拓学针对某安全管理体系进行评价，方楠等人[ ]基于软件的评价准则进行研究通过定性与定量相结合进行软件评价 。这些研究能更高效 地形成对特定行业领域的软件的评价体系，帮助相关企业完善复杂而繁琐的不成熟软件体系评价和分析难题，规范体系文件中不完善的指标与准则。

1 可拓学模型建立

1.1 建立评价指标体系

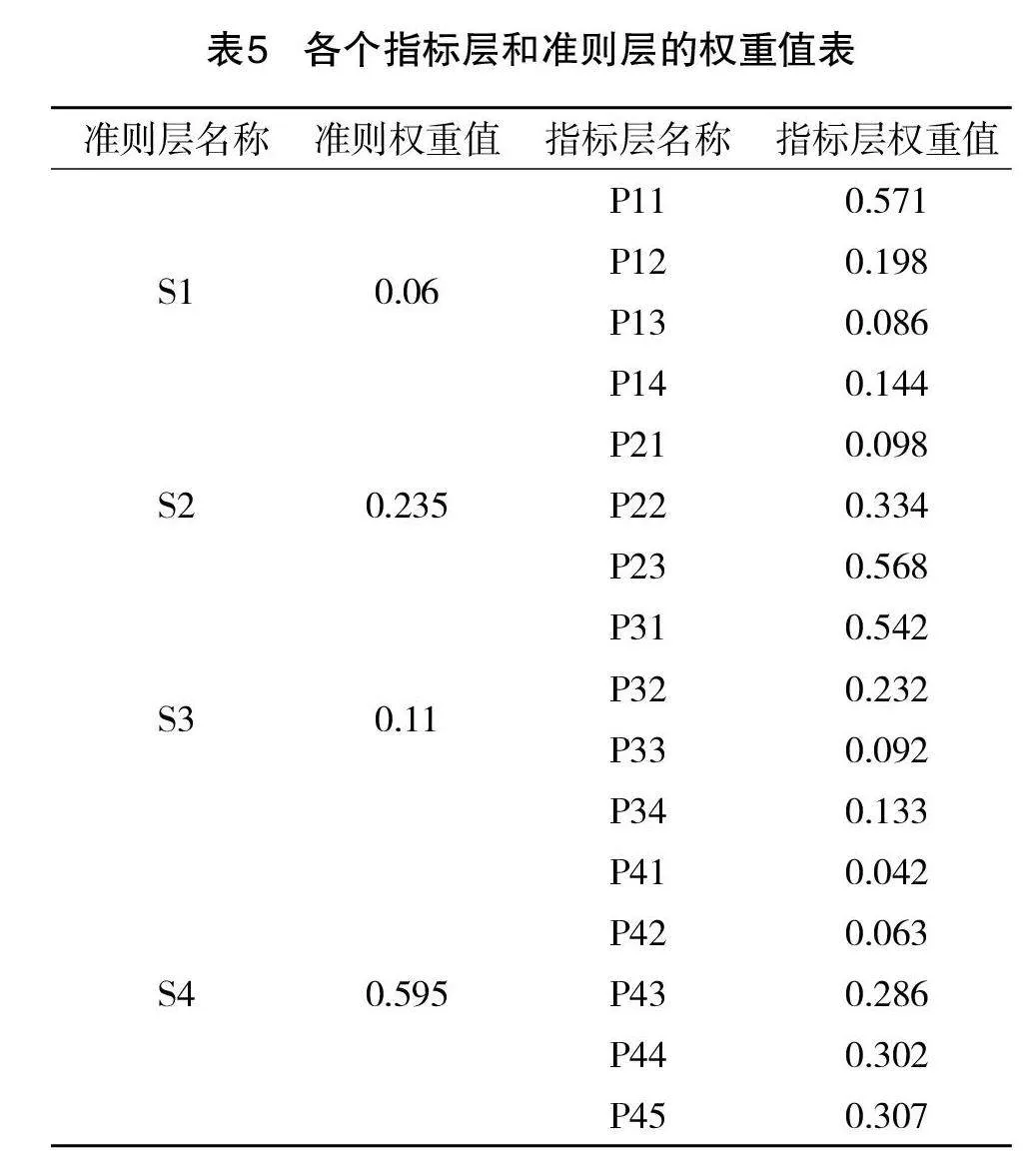
本文使用层次分析法（Analytic Hierarchy Process，AHP）[ - ] ，将相关的各项指标进行分解，再建立评价模型。该分析方法的基本结构模型进行定量分析，对该层不同的因素进行分析，最终综合比较确定最终指标因素，从而解决难以通过定量分析描述的复杂目标难题，为相关的企业和机构提供决策参考。本文结合企业实际软件裁剪工序、软件生产工况、软件工艺和管理要求以及专家和高级技术人员经验，确定软件裁剪体系评价指标。其中，准则层包括，软件人员培训与管理、软件设备操作与匹配、软件开发和工艺设计与拓展4个方面，评价指标共16项。

1.2 确定相关层次指标的权重

通过层次分析法（Analytic Hierarchy Process，AHP），确定相关指标层次的权重，利用专家打分法，邀请相关专家结合表2根据实际工况进行打分，得到各层指标之间的相对权重，以客观的评价相关体系。

G=[（G&S_1&S_2&S_3&S_4@S_1&1&1/5&1/3&1/6@S_2&5&1&3&1/4@S_3&3&1/3&1&1/7@S_4&6&4&7&1）]

CR=（C.I.）/（R.I.）

C.I.=（λ_max-n）/（n-1）

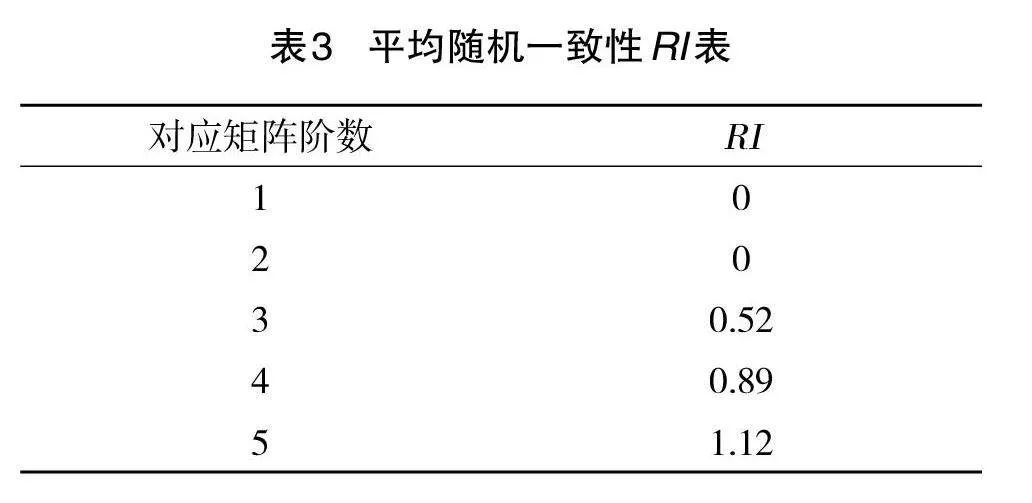
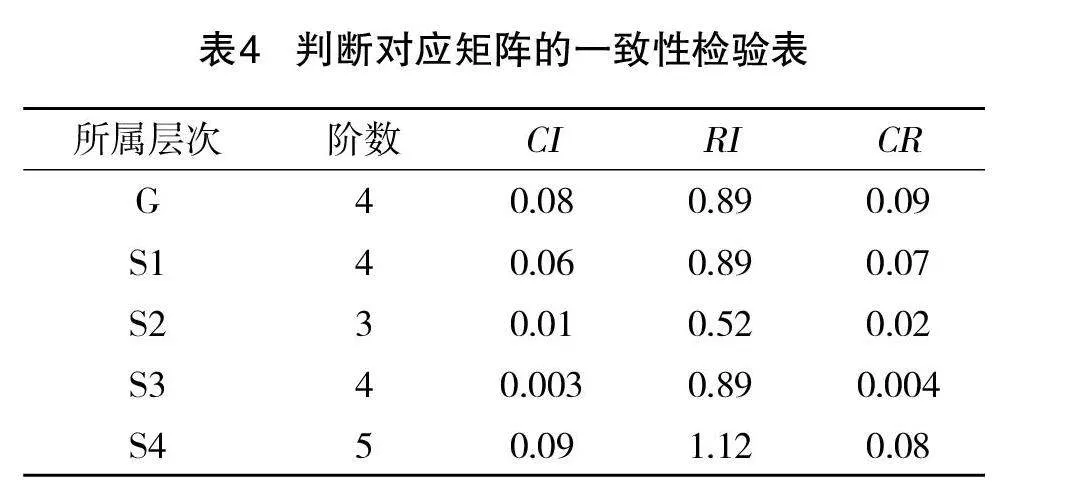
经计算G的特征值λ_max=4.23，根据表3选取n=4时的R.I.值为0.89

CR=（C.I.）/（R.I.）=（0.08）/（0.89）=0.09<0.1

据多次蒙特罗模拟得到随机一致性RI值如表3所示，首先对G层矩阵进行计算，通过python中的numpy库计算矩阵相关特征值，经验证，无须对矩阵进行修正，以此法分别对S1、S2、S3和S4进行验证，得到其一致性检验结果如下，其CR的值小于0.1，满足一致性要求。

1.3 建立可拓学模型

1.3.1 评价等级的确立

根据评价指标体系，准则层的评价因素结合G={S1，S2，S3，S4}，方案层的评价因素结合S1={P11，P12，P13，P14}，S2={P21，P22，P23}，S3={P31，P32，P33，P34}，S4={P41，P42，P43，P44，P45}。并建立评价的集合M={M1，M2，M3，M4，M5}={全面，比较全面，一般，待优化，极待优化}，分别对用其各自等级，并用I、II、III、IV和V这5个安全等级进行对应。

1.3.2 经典域、节域和待评物元

本研究的物元可拓模型主要根据可拓学中的物元理论、关联函数和可拓集合等理论为基础，将事物N、特征C、事物的量值V三者构成的有序三元组R=（N，C，V）作为描述事物的物元。并以此建立裁剪优化体系的相应经典域、节域物元、待评物元、安全关联度等，依据各裁剪体系指标的实际数据计算其体系待优化的等级。

具体的推导步骤如下。

R=（（N&（C_1@C_2@⋮@C_n ）&（V_1@V_2@⋮@V_n ）））=[（R_1@R_2@⋮@R_n ）]

R_j=（N_j，C_ji，V_j）=（（N_j&（C_j1@C_j2@⋮@C_jn ）&（V_j1@V_j2@⋮@V_jn ）））=（（N_j&（C_j1@C_j2@⋮@C_jn ）&（⟨a_j1，b_j1 ⟩@⟨a_j2，b_j2 ⟩@⋮@⟨a_jn，b_jn ⟩ ）））

R_p=（N_p，C_ji，V_p）=（（N_p&（C_j1@C_j2@⋮@C_jn ）&（V_p1@V_p2@⋮@V_pn ）））=（（N_j&（C_j1@C_j2@⋮@C_jn ）&（⟨a_p1，b_p1 ⟩@⟨a_p2，b_p2 ⟩@⋮@⟨a_pn，b_pn ⟩ ）））

R_k=（N_k，C_ji，V_ji）=（（N_k&（C_j1@C_j2@⋮@C_jn ）&（V_j1@V_j2@⋮@V_jn ）））（1）

式（1）中： 是评价对象第j个等级； 是在第j个等级下评价对象第i个特征； 是等级个数； 是特征个数； 是评价对象第j个等级 对应的特征值范围； 是评价对象的全体等级； 是评价对象第i个等级的下限值; 是评价对象第i个等级的上限值; 是第i个评价全体等级的下限值; 是第i个评价全体等级的上限值。

待评价物元体系：

（2）

式（2）中： 是待评物元名称； 是 关于待评物元的量值名称。

1.3.3 关联函数公式推理

（3）

式（3）中： 为待评价物元的第i个特征值。

1.3.4 确定系统的评价等级

针对于目标层G和准则层S的关联度计算公式如下：

（4）

式（4）中： 通过层次分析方法计算的权重；待评价的物元的安全等级为最大的 所对应的安全等级；目标层和准则层所对应的安全等级为 。

（5）

式（5）中： 评价目标的所对应的特征值，表明评价目标评定的等级与相邻等级程度的偏差； 为对应的评价的等级，I，II，III，IV，V。

2 实践探索应用

2.1 确定某裁剪软件优化系统的评价等级

本文以某科技公司的裁剪优化体系为例，对软件系统的指标层进行建模和评价，并要求相关专家进行打分，并对评价的指标取对应打分的均值，结果如下。

={71，86，81，89} ={65，62，82}

={83，92，61，69} ={68，72，67，86，93}

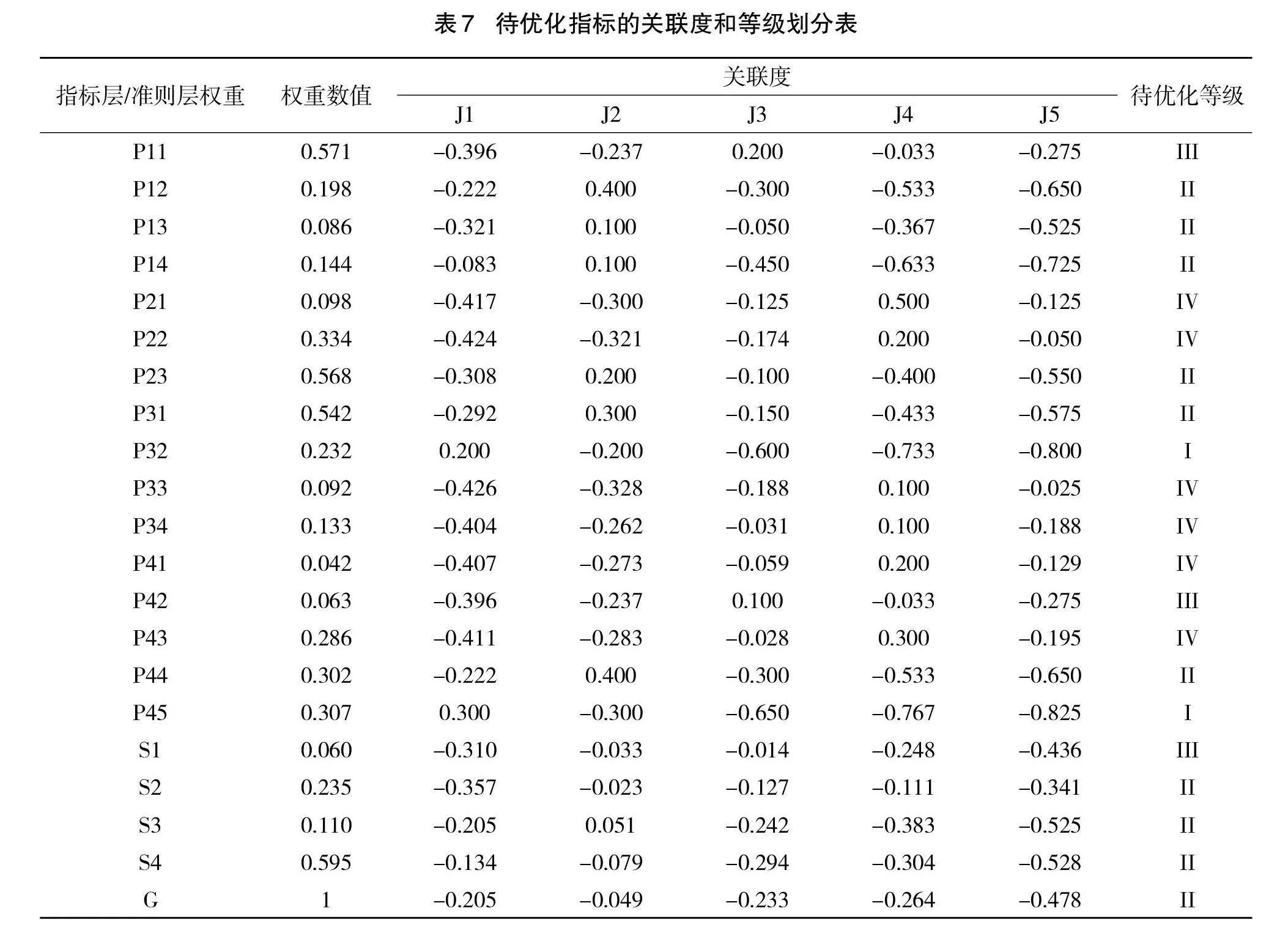
根据关联度计算结果显示，目标层G的整体裁剪软件模块体系等级为II级，整体软件模块体系较为完善。该企业的裁剪软件模块体系总体比较全面。但针对于相应指标层之下的决策层各项待优化等级，P21软件设备稳定性和P22软件关键刀具匹配、P41软件质量检验机制、P43软件工艺节拍设计、P33软件技术实施和P34软件开发成本和周期等方面，存在一定优化空间。

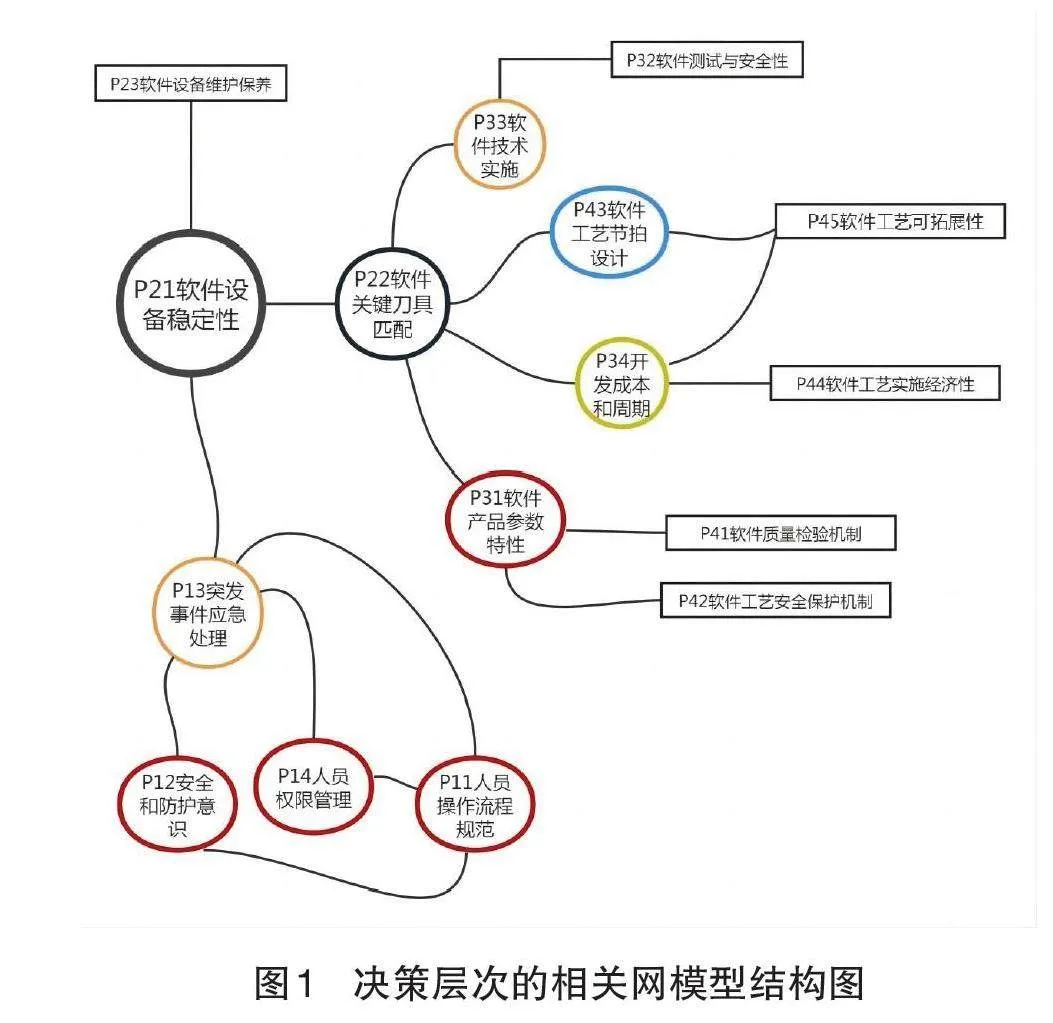
2.2 建立某裁剪软件相关网的模型

因发现多个待优化决策层，本次针对该软件体系，建立相关网络模型[ ]，从而分析主要矛盾。据该相关网模型可见，在所有待优化层次中，P22软件关键刀具与匹配在网中的影响因素较多，因此将P22层为主要矛盾进行优化，更能提高该裁剪软件体系模型的整体质量水平。

3结论与总结

通过建立软件模块的可拓学基元模型并根据关联度等，把本指标层和其下一层次复杂的定性问题转化为定量的数理计算问题，初步确定了该软件体系的综合等级、各指标层以及策略层分等级，发现需要优化的具体层次。但待优化层次较多，利用可拓学相关网模型理论，发现主要矛盾层级，并针对软件关键刀具匹配层进行优化改进。通过验证，能够提升小型裁剪模块的效率，降低设备刀具使用损耗。本次小型裁剪软件模块评价时已经是半成熟的模块，如能够在设计初期就结合可拓学模型对软件各个设计指标体系进行评价，可能会进一步减少中后期评审收等阶段的修改频次，极大提高软件模块体系的总体质量。

参考文献：

[1]冷超，徐小迪.采选充一体化质量评价体系软件开发与应用[J].山东煤炭科技，2022 ，40（4）：185-187.

[2]王燕妮，张振超，李静.基于可拓学的有限空间作业安全管理现状评价[J].安全，2023 ，44（9）：44-50.

[3]方楠.软件技术企业绩效评价体系研究[J].合作经济与科技 ，2023（8）：106-109.

[4]姬广东.层次分析法在直升机重量控制风险评价中的应用[J].中国科技信息，2024（6）：74-76.

[5]马轶旭.基于层次分析法的中小物流企业财务风险评价探讨[J].现代商业，2023（13）： 149-152.

[6]丁怡，朱弘扬.物元相关网在企业联盟合作模式选择中的应用[J].科技创新导报，2019， 16（28）：162-168 .