初中数学开放性题型教学探究

【摘要】数学开放性题型是数学教学中的一种新题型，它主要是相对于传统的封闭式的题型而言的，其教学的目的是促进学生素质的全面提高.它是一种新的教育理念在课堂教学中的具体体现.众所周知，数学教学不仅只是让学生能理解、能记忆，更重要的是培养学生的数学思维习惯、创新意识以及提高创新能力，引导学生积极参与、独立思考并且能自觉动手实践，它对学生开展研究性学习十分重要.

【关键词】开放性题型；初中数学；课堂教学

1 提供开放性的题目

教师在平时的教学中，在解答数学题时，要善于逐步渗透一些开放性解题的思想，坚持循序渐进地引入一些有研究性和探索性的问题，让学生在尝试中体会学习数学的乐趣，激发学生学习数学的兴趣.教师提供的开放性的题目一般要具备以下特征.

1.1 问题的结果不唯一

同一个数学问题，可以应用不同的解题思维.教师应该想方设法，引导学生展开联想，培养学生的发散性思维，找出多种结论.

例如 ①写出经过两点A （2，0）、B（0，-1）的一条抛物线的解析式；

②整数范围内的因式分解，如①x2+Mx－24；②x2+7x+N，则M，N可以取哪些整数？

1.2 解题的思想要开放

教师要运用各种知识的横向联系去解决同一实际问题，引导学生养成应用不同的思路和方法解决问题的习惯.举例说明：

请你设计几种不同的方案，测出池塘边两点AB之间的距离.

以上这一数学题，学生可以采用多种方法来解答，如等边三角形三边都相等的性质；平行四边形、矩形、正方形的性质；直角三角形的勾股定理；三角形的中位线的性质定理；相似三角形对应边成比例；解直角三角形等数学知识.在课堂上，教师可以慢慢地进行引导，开阔学生的思路，发挥学生的想象力，多角度、多方位、多层次地探求解题思路和方法，找到数学知识和实际问题的最佳切入点，从而达到培养学生创新思维、创新能力的目的.

1.3 解题的方法要开放

在解答问题的方法上，教师不要局限于一些解题的程序，注意引导学生使用不同的解决方法.如在初中梯形面积公式的教学中，教师可以通过“分解与组合”的不同解题思路把未知问题转化为已知问题（见图1－图9），同时，引导学生运用此种数学思想去寻求问题的多种解决方法，培养了学生数学方法的灵活性和开拓性.

2 探索解题方法，培养能力

开放性课堂教学，主要体现在：以教师为指导，以学生为中心.根据“提出问题—分析问题—解决问题—提出新问题”的结构来培养学生的解题能力.具体流程图如下：

2.1 创设问题情境 ，激发学生学习数学的兴趣

在学习内容上，教师应该选择与当前学习知识相关的实际问题作为学习的中心内容，创设问题情境，引起学生的好奇心，给学生一个需要立即去解决问题的动力.

例如 有理数章节的教学时，教者可从校运会篮球比赛某班队的进球数、失球数等实例引入正负数，因而激发学生学习兴趣，引导他们主动参与，从而进入学习最佳状态.

又如，在讲正多边形时，首先，教师可以展示一些由正多边形构成的美丽的图案.其次，向学生提出这样的问题：哪些正多边形可以用来设计铺地的瓷砖？要使铺成的地面既无空隙又不重叠的条件是什么？（条件是围绕每一个公共顶点的各角之和为360°，所以用一种正多边形为规格的瓷砖铺地，只能使用正三角形、正方形、正六边形三种）最后，引导学生使用不是正多边形的图案（平行四边形、矩形、三角形等）和几种正多边形混合而成的图等，不断引导学生在情境中愉快地、深刻地理解和掌握新学的知识，努力培养学生创造性思维的能力.

2.2 尝试探索，培养学生分析问题的能力

在引导学生解决所提出的问题时，教师不要直接告诉学生如何去解决所提出的问题的方法，而是尽量引导学生主动参与，不断地向学生提出带有启发性和挑战性的问题，给学生提供动手、动脑、动口的机会，逐渐地提供解决问题的有关线索，积极引导学生通过自学、观察、猜想、讨论、交流等方法来解决问的例题.

让学生在掌握知识的同时，教师还要教会学生怎样接受问题、分析问题、解决问题.

例如 在教学圆的相交弦性质和切割线性质时，可以通过对几何图形中某些元素位置的变化而引起的图形的演化来进行探索.第一，让学生在圆中画出两条相交弦（图11），作辅助线，同时，教师充分尊重学生的自主探索思路，并引导他们小组讨论出结论（如角相等、线段成比例、三角形相似），从而得出相交弦性质；第二，提出新问题：若两条弦的交点在圆外（图12），一条弦变成切线（图13），两条弦都变成切线时情况又如何变化（图14），当一条弦通过圆心时又有怎样的（图15和图16），又如何性质？教师不断地提出问题，不断地引导学生自主探索学习，使学生既能掌握所学知识，又能培养他们的解题能力.

2.3 解决问题，培养学生的思维品质

教师在让学生观察、猜想、分析、归纳、概括、探索、解决数学问题的全过程中，要善于让学生在学习中，经过自学、质疑、讨论、交流去发现问题，分析问题，从而得出一些猜想和结论，通过证明来解决问题，不断地提出新问题，引导学生不断地进取，培养学生良好的思维品质.

2.4 实践应用，培养学生思维的发散性和创造性

张玺恩教授曾指出：“数学教育给予学生不仅是知识，更重要的是在于使学生受到数学思维与教学思想方法的训练，提出问题，把实际问题抽象为数学问题进行分析，探索和解决.”因此，日常的教学中，我们要努力引导学生运用所学知识去仔细观察、细致分析和逐一解决实际问题.强化学生动手实操能力的培养，增强学生使用数学思维来解决身边实际问题的欲望，培养学生的发散性思维和创造性思维.

3 题目变式，提高解题素质

为扩大学生的思维空间，我们可把教材中学生熟知的例题、问题、训练题进行改编，变“封闭性题型”为“开放性题型”，进一步提高学生解决问题的能力素质.

3.1 改变命题的结构

教师可以采用以下方法，改变教材中的命题结构：

（1）基于课本的例题、训练题，我们可特意把原问题稍作改编，使该问题的答案多样化.

（2）去掉题目中的一个或多个条件，让学生去探求其结果成立的条件.

（3）去掉题目中得出的结果，使它答案非唯一.

（4）先给出结论，让学生去探求使结论成立的必要条件.

3.2 增强命题的探索性

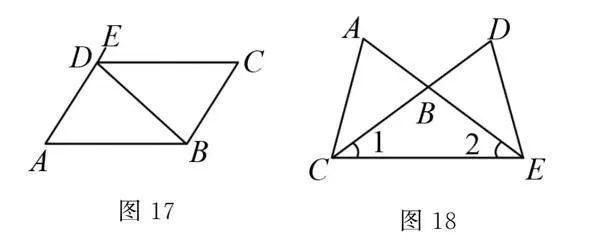
在例题教学中，教师尝试把多个条件进行组合和探究，从而激发学生的学习兴趣.例如：图17，要得到AB∥CD，只需满足条件（只填一个）；再如：图18，AB = DB，∠1=∠2，请你添加一个适当的条件，使△ABC ≌△DBE，则需添加的条件是？.

3.3 加强命题的变式训练

教师在教学中，还可以改变引导的方式，强化“变式训练”，让学生在变化中去体验、探求.

例如 在探讨对角线互相垂直且相等的四边形是正方形，就可以向学生提问：当对角线发生变化时，四边形又如何变换？另外，教师可以设计结论发生变化时，如正方形改为平行四边形、矩形、菱形时，条件又如何变换？最后，还可以向学生提问：除对角线外，还有什么条件判定一个四边形（平行四边形、矩形、菱形）是正方形？这样随着问题的不断深入，让学生产生一种好奇心，兴趣盎然地去自主思考、自主探究.

4 结语

总之，在全面推进素质教育的今天，如何探索课堂教学模式，培养和发展学生的创造性思维，是摆在我们每一位数学教师面前的一项重要任务.教师只有切实转变教育观念，优化课堂教学，充分调动学生学习数学的积极性，才能让学生主动地参与学习的全过程.教师只有注重引导、鼓励学生敢于提出问题，勇于探索求异，善于应用数学思想去解决一些实际问题，才能促使学生养成良好的数学思维习惯，培养创新意识，提高创新能力，使学生积极参与、独立思考并且自觉动手实践.这为学生以后的终身学习，打下了一个坚实的基础.

参考文献：

［1］曲培富.数学教学中“教为主导、学为主体”的认识与实践［J］.中学数学杂志，1993（01）：13-14.

［2］肖柏荣.数学教育设计的艺术［J］.数学通报，1996（10）.

［3］张行涛，周卫勇.新课程教学法（中学卷上册）［M］.北京：中国轻工业出版社，2004.

［4］张立兵.新课程怎样教［M］.北京：开明出版社，2003.