培养学生数学兴趣的方法探究

【摘要】数学是基础教育课程中一门最基本、最重要的学科，而学好数学又离不开数学兴趣的培养.本文先论述培养学生数学兴趣的重要性，兴趣的本质，然后结合教师的教学实践探究培养数学兴趣的方法的四个方面.教师只要培养出了学生的数学兴趣，就能教会学生思维的方法和努力探索的精神，使学生的素质得到全面提高.

【关键词】兴趣培养；初中数学；学生培养

1 引言

21世纪，中国全面进入了一个新的发展与竞争的时代，归根结底，是人才的竞争和知识的竞争.而数学知识又是这些知识中最基本、最重要的知识.数学家拉普拉斯说过这样一段话：“数学是一种手段，而不是目的，是人们为解决科学问题而必须精通的一种工具”.又如华罗庚教授所说：“宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，生物之谜，日月之繁，无处不用数学.”可见数学知识在日常生活及其生产技术中应用的广泛性与重要性.

2 学习兴趣研究及培养

兴趣是学习的强大动力和内在力量，是推动学生自觉学习的动力.只有当学生本身对学习发生浓厚的兴趣时，才能使整个认识活动兴奋起来，促使他们去追求知识，探索科学奥妙，增强学习情绪和克服困难的意志，从而提高学习效率.

我国的大教育家孔子早已指出：“知之者，不如好知者；好之者，不如乐之者.”意思是说，对于学识，懂得它的人不如喜欢它的人，喜欢它的人又不如醉心于它，以它为乐的人.教育家蔡元培也主张：“我们的教书，并不是像注入水瓶一样，注满就算完事，最主要的是引起学生读书的兴味（如果引起学生的兴味了），做教员的竟不讲也可以.”从当前教学状况来看，学生在学习上花时多，负担重，质量却不高.究其原因，无不与学习兴趣有关.凡具有强烈兴趣的学科，学业成绩明显地好，并且学得活，能做到举一反三，触类旁通.兴趣比智力更能促进学生勤奋学习，从而取得优秀的学业成绩.兴趣能使个体的整个心理活动积极起来，处于“最佳状态”，从而促进智力的个体发展，著名心理学家皮亚杰十分重视兴趣对智力的作用，他指出：“……所有智力方面的工作都要依赖于兴趣.”由此可见，兴趣的培养对学生学习具有重要意义.

然而在教学实践中应如何培养学生学习数学的兴趣呢？下面是笔者从教三十多年，针对培养学生数学兴趣的方法进行的一些探究.

2.1 悬念引申，激发数学兴趣

强烈的好奇心，是引发兴趣的重要原因，它可以紧紧抓住人的注意力，使其在迫不及待的情绪中积极探索事情的前因后果及内涵.一节课的良好开端，不仅具有画龙点睛的作用，还有制造悬念的效果，使学生的学习兴趣在上课伊始就被引发起来.悬念的设置能激发学生的学习动机和兴趣，使思维活跃，想象丰富.

例如 在讲解有理数的乘方运算时，教师拿出一张仅有0.1mm厚的纸，说：把它反复对折27次后，估计一下厚度会有多高呢？下面有的学生估计有课本厚，有的估计有墙厚，只有一个学生说比较厚，说大约有教室的高那么厚，结果引来了学生的笑声，讨论热烈.但当教师说出它的厚度将大于世界最高峰——珠穆朗玛峰时，全班学生都惊呆了，一张纸反复对折，能有珠峰的高那么厚吗？想让教师论证.在学生的密切注意下，教师写出：纸对折一次厚度为0.1×2=0.2mm，对折两次厚度为0.1×22=0.4mm，……当对折27次时，其厚度为y=0.1×227=134217728mm=13421.7728m，大于珠峰高度8848m，使学生们都在强烈的求知欲望下学习了有理数的乘方，悬念把他们引入了诱人的知识境界.在教师的引导下，学生的好奇心由潜伏状态，诱发为活动状态，投入到良好的学习情境中，产生了良好的效果.正如苏霍姆林斯基说的：“惊讶感情——是寻求知识的强大源泉.”悬念的作用在于学生了解学习的目的性，激发学生学习兴趣.设置悬念时，要富有启发性、趣味性、惊奇性，还要注意学生认知事物的规律性.

2.2 设置矛盾，诱发学习数学的兴趣

数学论指出：“在学生已形成的概念，他们对某些问题的生活经验和对该问题的更科学、更精确的解释之间树立矛盾，是激发学生学习兴趣的有力手段.”学生运用自己智慧克服困难越多、越大，兴趣就越高.

在讲解例题，布置作业时，有意识地设置“陷阱”，能有效地引起学生对某些易忽视的概念、公式和条件的重视，激发他们的学习兴趣，提高判断正误的能力.

例如 在学习分式方程解法时，教师出示了这样一道题：

解分式方程：x+1x2+2x+1=x+1x2+2x+2.

解 方程两边都除以x+1，

得1x2+2x+1=1x2+2x+2

去分母、化简，得：

x2+2x+2=x2+2x+1

移向、合并同类项，得2=1.

当教师把这样一个结果板演到黑板上时，全班学生鸦雀无声，解题过程好像没有问题，而结果却是大大的矛盾.带着疑惑，学生急于想知道为什么，然后教师再讲解分式方程的解法和应注意的问题.这样设置矛盾，引起学生的数学兴趣，其效果是不言而喻的.为了解决类似这样的矛盾，学生必须认真听教师讲解，随之而来的是，使他们在实践中辨别真伪，认真思索，努力解决矛盾，达到对知识的深化和巩固，诱发学生的求知欲，产生浓厚的数学兴趣，越学越爱学，越学越有趣.

2.3 一题多解，激发学生数学兴趣

要培养学生学习数学的兴趣，教师还应不断地改进教学方法，深入理解和钻研教材，引导学生探索多种解题方法，开拓视野，把知识有机地结合起来.

例如 讲了乘法公式后，教师出了这样一道题：用多种方法求出（a+b）2（a-b）2的值.

解法1 a+b2a－b2

=a2+2ab+b2a2－2ab+b2（完全平方公式）

=a4－2a3b+a2b2+2a3b－4a2b2+2ab3+a2b2－2ab3+b4（多项式的乘法）

=a4－2a2b2+b4 （合并同类项）.

很明显，这种方法比较繁琐且易出错，属于一般的解法，用此方法解答的学生对知识只是一般的了解，不够灵活.

解法2 a+b2（a－b）2

=a2+2ab+b2a2－2ab+b2（完全平方公式）

=a+b2+2aba2+b2－2ab（转换平方差公式）

=a2+b22－4a2b2 （平方差公式）

=a4+2a2b2+b4－4a2b2 （完全平方公式）

=a4－2a2b2+b4（合并同类项）.

这种方法较前者简便些，考虑到用乘法公式（特别是转换为平方差公式）来解，能省去繁琐的运算步骤，但要求学生对各种公式熟练掌握.

解法3 （a+b）2（a-b）2

= a+ba－b2 （结合幂的运算性质转换）

=a2－b22（平方差公式）

=a4－2a2b2+b4 （完全平方公式）.

比较三种解法，此种方法最简捷，先转化为积的乘方，再用平方差公式和完全平方公式.这就要求学生对知识要深入理解，熟练掌握并且思维敏捷.

经过比较，大家公认最后一种方法最佳，然而最佳方法的掌握要求学生对乘法公式不但要熟练掌握，更要进行系统化的思维活动，运用智慧进行概括方能做到“灵活运用”.灵活运用使学生在思维的灵活性和创造性中看到了知识的力量，尝到了甜头，也对数学更加感兴趣了.

2.4 一题多变，深化学生的数学兴趣

教师在课堂教学中，必须创设最佳思维情境，造成学生求新知识的心理状态.课堂要注意“思”与“变”.一道好的数学题，教师要充分发挥其效应，采用多变的方法，培养学生学习的兴趣.如一道数学题可变换条件、结论等近似或相反的许多题目，以结合各方面的知识，把学生引入胜境，开拓知识视野，做到解一题知一类，达到触类旁通的效果.这种拓宽问题、深化知识的教学常常能推出新的规律，使知识得以推广，并在推演的过程中培养学生良好的思维品质，形成良好的学习习惯，产生学习兴趣.

例如 在学生刚刚学完平行线的性质时，教师出示了这样一题：

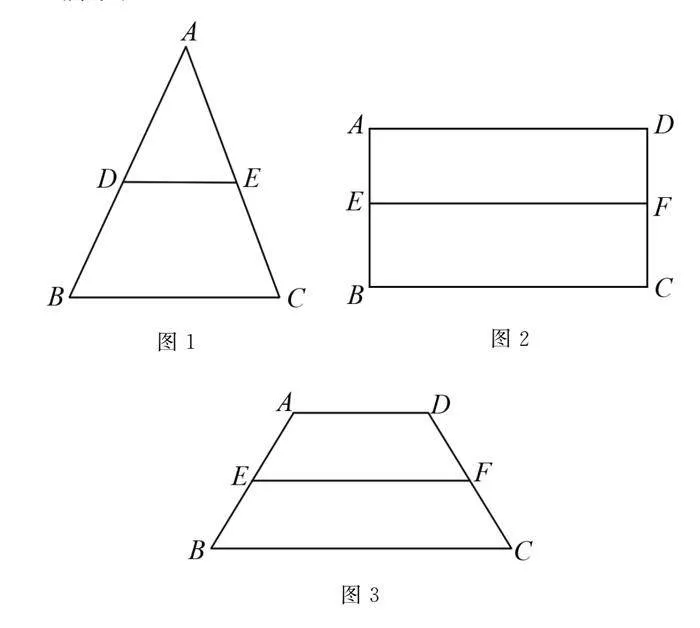
如图1所示，D是AB的中点，DE∥BC，请你通过测量比较AE和CE的长度有何关系，你得出了什么结论？当学生得出AE = CE = （ ）cm时，教师把题设变为：若把三角形换成长方形，如图2所示，

E是AB中点.EF∥BC，AD和EF平行吗？为什么？经测量，你发现DF和CF有什么关系？在学生得出正确结论后，教师又把题设换为，若把长方形换成梯形，如图3，E是AB的中点，EF∥BC ，那么AD和EF平行吗？为什么？经测量DF，CF，你发现有什么关系？

这样一题变换了三种图形，而学生却得到了一类题的解法，这为学生以后学习平行线等分线段定理作了良好的铺垫.这种由浅入深，由表及里，由横到纵，由正到反的练习，增强了学生学习数学的兴趣、学好数学的信心，提高了克服困难、解决问题的能力，经历了学习、探索、成功的过程，其乐无穷.尤其是差生，当他们感受到了有能力通过自己的思考把问题弄明白时，也就产生了学习的兴趣，认识到数学并不是枯燥无味的，而是学有所乐，乐在其中，使他们完成了由没有兴趣到感兴趣，由不爱学到爱学，由学不会到会学习的转变.

3 结语

数学学习既有苦的探索，也有甜的享受，为了掌握某种技能和方法，学生需要做大量的练习，为了提高解综合题的能力，更需要长时间地去苦思，去探索，因此保持长久地学习兴趣很重要.教育家赫尔巴特指出：教育应当贯穿在学生的兴趣当中，使学生的兴趣在各阶段都能连贯地表现为注意、等待、探究和行动，兴趣是教学的手段，又是教学的目的.“兴趣是学习的先导.”学习兴趣有动力作用，会推动学生满腔热情地进行钻研.教师在教学过程中尽力挖掘数学内容中的兴趣因素，注重激发学生学习数学的兴趣.学生只要有了学习数学的兴趣，才会主动、自觉、积极地地去学习，这也可以说是学好数学的必备条件.在这样的数学教学中，学生既得到了知识，学会了思维的方法，又培养了他们克服困难、努力探索的精神，使他们的数学素养得到了全面提高.

参考文献：

［1］李淑文.中学数学概论［M］.北京：中央广播电视大学出版社，2003.1.

［2］叶奕乾.心理学［M］.北京：中央广播电视大学出版社，1995.2.

［3］王道俊、王汉澜.教育学［M］.北京：人民教育出版社，1989.12.

［4］苏霍姆林斯基.给教师的建议﹙全一册﹚（杜殿坤编译）［M］.北京：教育科学出版社，1984.6.