以问题为导向，促进深度学习

【摘要】课堂问题是数学课堂教学的重要手段，它在激发学生学习动机、引导学生深度思考、培养学生高阶思维等方面发挥着重要作用.课堂提问为学生提供了独立思考和合作交流的机会，为开展深度教学提供了前提.在课堂教学中，教师应结合教学实际精心设计问题，让学生在问题的探索中领悟数学本质、积累数学活动经验、提升数学素养.

【关键词】课堂提问；深度教学；数学素养

在传统课堂教学中，部分教师认为提高学生学习能力、培养学生数学思维能力的捷径就是“多讲多练”.然而“多讲多练”易使思维固化，不利于学生的长远发展.为改变这一局面，教师应创设有意义的教学情境，提出有价值的“课堂问题”，以此在问题的驱动下促进深度学习，培养学生勤于思考的习惯，提升学生的综合素养［1］.笔者在教学“图形的旋转”时，围绕旋转的本质特点精心设计课堂问题，让学生在问题的探索中挖掘知识本质，发展学生核心素养.

1 教学分析

旋转是继平移、轴对称之后的又一图形运动.学生通过前面两种图形运动的学习，已经有了一定的变换思想，加之初中生具有一定的观察、分析、抽象能力，这为“生本”课堂的开展提供了便利.在教学中可以从学生已有的知识、经验出发，引导学生运用类比方法来探究旋转，这样从学生熟悉的内容出发不仅可以巩固探究方法、强化认识，而且可以降低学习的难度，激发学生对数学探究的兴趣，同时通过有效的类比可以将三种运动有机地结合在一起，让学生深刻地体会三者之间的异同.不过，虽然类比设计好处很多，但是难免会缺少一些创新和内涵.在本课教学中，教师围绕“旋转”这一本质属性设计核心问题，让学生在问题的引领下去发现、去探索，逐渐揭开“旋转”的神秘面纱.

2 教学简录

2.1 认识旋转

师 你们能列举一些生活中有关旋转的例子吗？

生1 摩天轮、风车.

生2 转动的风扇.

生3 地球自转、公转.

……

师 非常好，那么你们能在网格纸上画一些旋转的图形吗？教师预留时间让同学们动手画图，并与同桌进行互动交流.

师 结合旋转实例及创作成果，你能用语言来描述它们的运动过程吗？（学生积极思考）

生4 围绕一个点转动.

生5 围绕一个点转动一定角度.（生补充道）

师 还有其他不同意见吗？

设计意图 引导学生从生活实际出发，通过感知生活中的旋转，逐渐抽象旋转的定义.这样在师生、生生的互动交流中，抽象的概念变得更加生动、形象，更易于学生理解和接受，使课教学更堂生动、活跃.

2.2 探究旋转

师 这里有个旋转，结合视频说一说它的运动过程.（教师投影展示三角形绕某点旋转的视频）

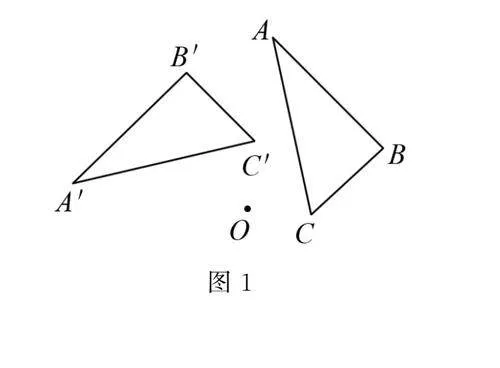
生1 如图1，△ABC绕点O逆时针旋转90°得到△A′B′C′.

师 很好，它是否满足旋转的定义呢？

生齐声答 满足.

师 观察图1，说一说旋转前后哪些量不变？

生2 旋转前后，△ABC的形状没有发生改变，它与△A′B′C′全等.

师 很好，那么除了看到△ABC在旋转以外，还有其他变换吗？（学生沉思）

生3 线和点也在作同样的旋转.

生4 图形和线是有无数个点组成的，所以当图形转动时，点也在转动.

师 大家说得非常好，分析得非常透彻.现在我们从点的角度思考，你能发现怎么样的结论呢？

师 图形中有无数个点，大家在思考问题时可以从某一个具体的点出发，看看通过这个具体的点的运动过程，你能得到什么结论？猜想那些无法具象的点会怎样变化呢？

以上问题具有一定的开放性，教师预留充足的时间让学生思考、交流，教师采集素材展示.

生5 点A绕着点O逆时针旋转90°到A′，点B绕着点O逆时针旋转90°到B′，其他点亦是如此.

生6 ∠AOA′=90°，OA=OA′；∠BOB′=90°，OB=OB′；∠COC′=90°，OC=OC′.其他对应点亦是如此，因为它们绕O点转动，所以O点到它的距离相等.

师 非常好的发现，你能进一步总结一下吗？

生7 旋转前的点与旋转后的点到O的距离相等，它们形成的以O为顶点的角的度数均为旋转角.

师 还有吗？（生表示没有其他发现了）

师 比如由OA=OA′相等，你能够得到什么结论呢？（教师及时提示，引导学生进一步探究）

生9 连接AA′，在△AA′O中，OA=OA′，点O在AA′的垂直平分线上.

师 很好，通过研究点的旋转我们发现了这么多结论.现在再看图形，此时可以怎样理解旋转呢？

生10 在图形旋转时，与图形相关的所有元素也发生着同样的变化.而图形是由点组成的，所以其本质是点的运动.点怎么动，图形就怎么动；反之，图形怎么动，点也怎么动.

师 在之前我们也有过类似的经验，课后大家不妨将这三种运动进行类比，看看你有哪些收获.

设计意图 在教学中，教师引导学生思考图形变换与点变换之间的关系，引导学生通过对点的运动变化来刻画图形的变化，凸显数学本质.在教学中，教师将类比学习的机会交给学生，让学生将新、旧知识串联起来，通过类比明晰三种运动的区别与联系，进而将新知纳入到原有认知体系中去，培养学生的自主学习能力［2］.

3 结语

在本课内容学习前，学生已经有了平移、轴对称的学习经验，为此在具体教学中大多教师会运用类比思想展开教学.虽然通过类比学生也能很好地理解相关的概念，但是直接运用类比，似乎缺少一些新意，难以凸显问题的本质.另外，初中生已经具备了一定的类比分析能力，为此教师可以将类比学习的机会交给学生，这样既可以提高学生的自主学习能力，又可以让学生通过进一步探究深化对知识的理解.

总之，教师应以学生发展为目标设计教学活动，引导学生通过思考、探索、交流等方式揭示数学本质，进而提高学生学习能力，发展学生基本素养.

参考文献：

［1］陈柏良.构建深度学习的数学课堂［J］.中学数学教学参考，2017（11）：14-17.

［2］祝艳.教学之“法”，贵在“以生为本”——核心素养视角下对初中数学教学的思索［J］.数学教学通讯，2019（2）：35-36.

［3］李勇.类比思想在初中数学中的应用研究［J］.中学数学（初中版），2020（9）：27-28.