基于混流生产的农机制造物料配送期量优化研究
王保森 吕锋 张雷雷


摘 要:针对传统物料配送方式难以满足农机制造混流生产的问题,提出多品种小批量的物料配送期量优化方法,解决农机制造商仓储中心向线边配送物料过程中存在的配送总成本高、线边库存大、配送不及时等问题。以配送总成本、AGV配送小车装载空置率为优化目标,构建了多目标、多频次、小批量物料配送期量优化模型。根据模型决策变量的特征,设计了改进种群初始化生成方法和改进收敛因子的多目标灰狼优化算法,提高了算法寻优和收敛能力。实例验证了模型和算法的可行性和有效性。研究结果表明:较优化前,总配送成本减少21.3%,平均配送间隔期缩短23.4%,减少了库存积压和浪费,实现了多品种物料配送期量优化,有效降低了配送总成本。
关键词:农机制造;混流生产;配送期量;线边配送;多目标灰狼优化算法
中图分类号:F252.14 文献标志码:A
DOI:10.13714/j.cnki.1002-3100.2024.13.001
Abstract: In response to the problem of mixed agricultural machinery manufacturing mixed production methods, it is difficult to meet the problem of agricultural machinery manufacturing mixed production. Large, not timely delivery and other issues. Based on the total delivery cost and the vacancy rate of the loading of the AGV delivery car as the optimization goal, the optimization model of multi-target, multi-frequency, and small batch material distribution period is built. According to the characteristics of the model decision variable, the multi-target grey wolf optimization algorithm that improves the group initialization generation and improves the convergence factor has been designed, which improves the ability of algorithm and convergence. Examples verify the feasibility and effectiveness of the model and algorithm. The results of the study show that before optimization, the total distribution cost is reduced by 21.3%, and the average distribution interval is shortened by 23.4%, reducing the backlog and waste of inventory, the optimization of multi-variety material distribution period, and effectively reduced the total delivery cost.
Key words: agricultural machinery manufacturing; mixed flow production; delivery period; lineside delivery; multi-objective grey wolf optimization algorithm
0 引 言
为了快速响应客户多样化的需求,提升企业竞争力,多批次、小批量的混流生产已成为农机制造业的主攻方向。混流生产模式下的农机制造需要物料配送经济、快速、准确、有序、齐套地满足生产对物料种类、数量、时序、地点的动态需求。传统的物料配送方式是以经验为主,人为地制定配送计划,易产生配送批量不合理、线边库存高等现象,造成人力、物力等资源浪费问题,直接影响了生产效率和成本。因此,研究基于混流生产的农机制造物料配送期量动态优化方法,实现物料配送期量的智能决策,对提升农机制造生产效率具有重要的意义和价值。
针对生产制造的物料配送问题,国内外学者进行了广泛的研究。张艳姣等[1]研究了农机制造业仓储缓冲件库存控制策略。马艳丽等[2]开展考虑成本最优的物料配送方式研究。王昀睿等[3]通过对混流装配车间物料配送环境进行分析,解决混流装配车间配送不及时、费用高等问题。胡小建等[4]研究了以工位为中心的配送优化路径。杨晓英等[5]研究了农机制造多供应商配送多物料至核心制造商的物料配送模式。葛妍娇等[6]研究了基于智能感知网的物料配送动态优化模型。王金宇等[7]研究了与混流生产相适应的供应商直供线边物料配送动态期量优化问题。张世文等[8]提出一种基于实时定位的物料配送方法。WANG Y等[9]提出一种基于数字孪生的物料配送系统模型构建方法。MULLER等[10]在考虑软时间窗的基础上,研究物料配送多目标优化问题。
以上研究成果对物料配送问题在生产制造中的应用进行了深入的研究。国内研究侧重于针对传统的配送方式进行优化建模求解,国外研究多从物流成本入手设计合理有效的物料配送方案。现有研究很少涉及多品种物料的特性对成本影响的研究。鉴于此,本文在综合考虑混流生产的复杂性和物料本身特性的基础上,构建了能够满足混流生产需求的物料配送期量优化模型和算法,为农机制造的物料配送科学决策奠定理论基础。
1 问题描述
农机生产所需的物料储存在仓储中心,仓储中心负责存储物料并根据各工位对物料种类、规格、数量和时间等需求信息实施配送,配送过程由AGV小车完成。物料在仓储中心先由工人对物料进行分拣装车出发,再由AGV小车送至生产车间线边存储区,最后由生产线装配工人进行装配。
由于农机生产为多品种、多物料的混流生产,设置混流生产计划为U,w,r,其中:U为q机型的产量,w为q机型p物料的单机装配量,r为生产节拍。物料配送需要满足混流生产的计划需求,避免缺料停线现象发生。因此,与生产计划适应的配送期量是核心,以Nr,tr,Nr和tr分别为生产节拍r时的物料配送量与配送间隔期。物料配送问题模型如图1所示。
配送小车容量有限,各装配工位线边库存空间有限。求解满足生产物料需求的基础上配送过程配送总成本和配送间隔期最小。且假设:(1)各生产线工位的物料需求已知;(2)在一个计划期内,制造商生产计划确定,生产线按节拍生产,不发生停线现象;(3)AGV小车从仓储中心出发,完成配送后返回;(4)物料配送量体积不能超过AGV小车的容量限制。
2 模型构建与符号描述
2.1 参数设置
U为q机型的生产数量,Nr为节拍r时小车单次物料配送量,V为AGV小车容量,V为机型p配件占据的体积,C为小车单次使用成本,C为物料的单位库存费用,q为机型种类索引且q∈Q,p为物料种类索引且p∈P,L为从仓储中心到所需物料工位的距离,S为p物料对应的装配工位安全库存,tr为配送时间间隔,t为q机型p物料的单位分拣时间,r为生产节拍,v为小车行驶的速度,w为q机型p配件的单机装配量,I为q机型p配件的线边最大储存量,μ为AGV小车装载空置率。
2.2 模型构建
以配送总成本f与AGV小车空置率μ为优化目标,综合考虑生产计划物料需求的数量、AGV小车最大承载量、线边库存等约束条件,建立不同机型q不同物料p的物料配送优化模型。
(1)配送成本C为AGV小车在一定时间内配送总次数乘以单次配送成本。
C=cxy (1)
(2)线边库存成本C为各个线边平均库存水平与单位库存成本乘积。
C=+Sc (2)
(3)f表示配送总成本。
f=c++Scxy (3)
(4)AGV小车装载空置率。
μ= (4)
(5)tr为配送间隔期。
tr= (5)
综上,建立多目标物料配送模型:
F=minf∪minμ (6)
s.t
y=1 (7)
≤Nr (8)
Nr×V≤V (9)
Nr≤I (10)
+Nrt≤tr≤ (11)
式(6)为以配送总成本最小、装载空置率最小的多目标函数;式(7)表示每个工位都能被服务到;式(8)表示每种物料的单次配送量满足配送期间的消耗;式(9)表示单次配送体积小于小车容积;式(10)表示单次配送量限制,单次配送数量小于工位最大储存量;式(11)表示每个物料的配送周期需满足在最小和最大配送周期之间。
3 改进多目标灰狼优化算法设计
多目标灰狼优化(Multi-Objective Grey Wolf Optimizer, MOGWO)算法是MIRJALILI等受狼群合作捕食过程启发而提出的智能优化算法,用于解决多目标优化问题[11]。然而在使用标准算法进行求解时,多约束条件会使得算法陷入局部最优,解无法算出。
算法的核心及改进过程如下所示:
(1)改进初始化灰狼群体生成方式
本文的物料配送优化问题是非线性多约束问题,为了避免出现早熟收敛问题,引入差分进化[12]的过程提高算法的性能。生成初始种群具体过程如下:随机生成一组初始种群P:
P=P,P,…,P (12)
其中:P=x,x,…,x,表示第i个个体的D维位置向量。其中l和u分别表示第i个维度的上界和下界。选取两个不同的个体P和P,其中j≠k。生成一个差分向量v:
v=P-P (13)
利用差分向量更新当前个体P的位置,得到一个新的个体Q,F为缩放因子,取值为0,2。将适应度高的个体Q保留在新种群Q中,替换适应度低的个体P。
Q=P+F×v (14)
(2)设置适应度函数
为了使不同指标之间具有可比性。对两个目标函数f和μ进行归一化处理,可得f和f:
f=f-minf/maxf-minf (15)
μ=μ-minμ/maxμ-minμ (16)
确定归一化后的适应度函数为:
fitness=f×θ+μ×θ (17)
其中:θ+θ=1,且θ,θ取值范围为0,1。
(3)计算每个灰狼的适应度值
fitnessi=fitnessX (18)
其中:fitnessi表示第i只灰狼的适应度值,X表示第i只灰狼的位置。
(4)改进灰狼位置和速度生成
①包围猎物。灰狼在包围猎物时先确定自己的位置与猎物的距离。算法中,灰狼位置的计算方式如下:
D=C×Xt-Xt (19)
Xt+1=Xt-A×D (20)
A=2a×r-a (21)
C=2×r (22)
D为灰狼与猎物之间距离,X为猎物的当前位置,a为收敛因子。改进收敛因子具体表达式如下:
a=a-a×cos (23)
a,a为收敛因子最大值和最小值,t表示当前迭代次数,Maxit表示最大迭代次数。
②进行狩猎。通过考虑α、β和δ这三个最好的解的位置,随后引导其他灰狼判断猎物所在位置并进行狩猎。
4 实例验证及分析
4.1 实例数据
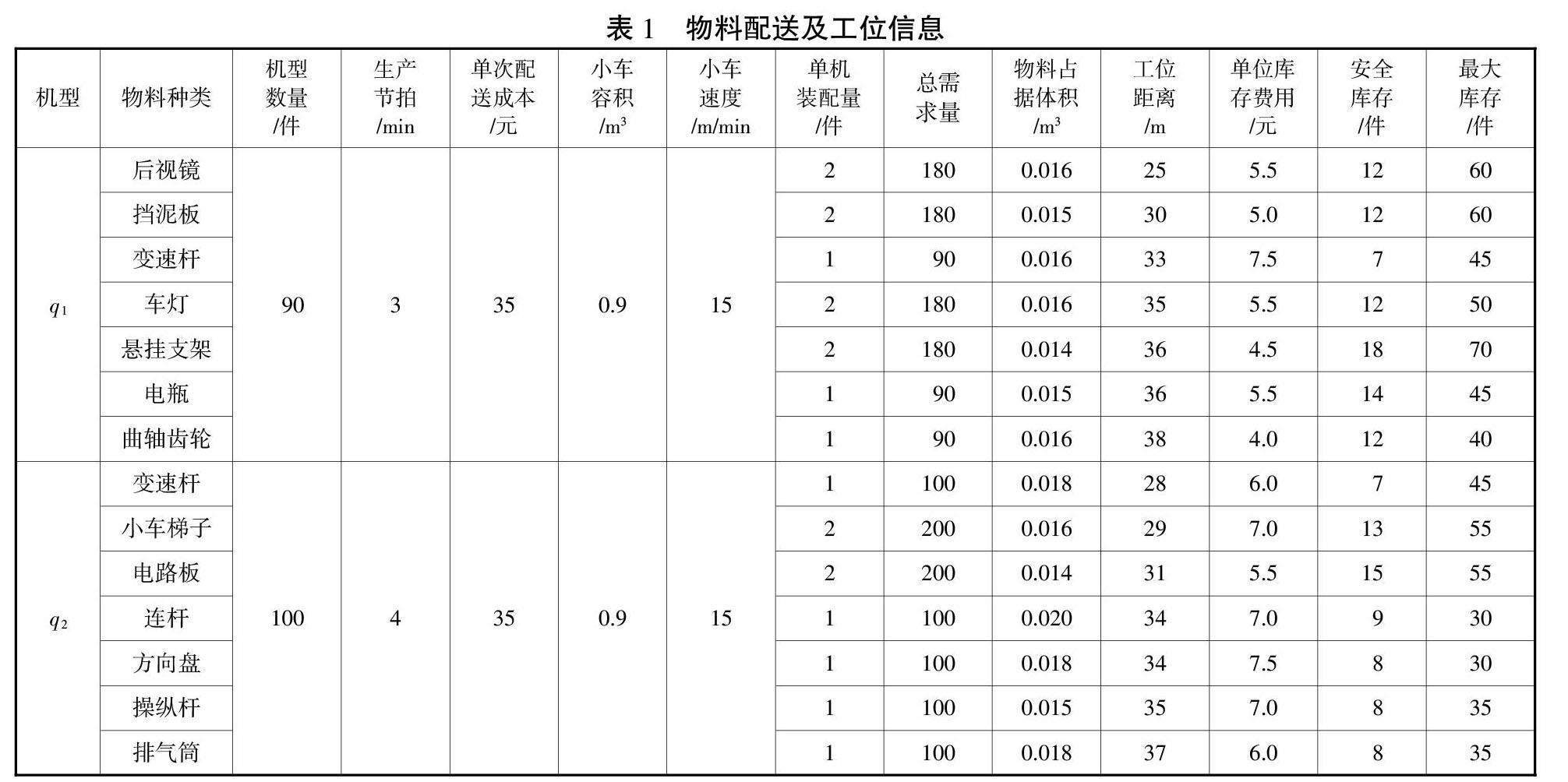
某农机制造企业生产车间采用混流生产模式,各物料的需求不同。选取其中2种机型14种关键物料进行验证研究。车间q1机型生产计划总量为90台,生产节拍为3min/台,车间q2机型生产计划生产总量为100台,生产节拍为4min/台。物料配送及工位信息和物料需求信息及参数设置如表1所示。
4.2 算法应用及效果分析
(1)仿真实验
采用MATLAB软件运行上述改进MOGWO算法,对参数进行设置:设置种群大小为100,最大迭代次数为300,网格膨胀参数为0.1,每个维度网格数为10。运行标准MOGWO算法和改进MOGWO算法得到目标函数收敛过程如图2所示。
(2)算法对比
改进MOGWO算法种群在85代收敛至最优解,标准算法在120代收敛,改进算法的收敛速度更快。对比标准算法和改进算法分别求得的目标函数适应度值大小,改进算法的函数适应度值更小,优于标准MOGWO算法,验证了算法的有效性和优越性。
(3)优化结果
优化后,求得的Pareto解集如图3所示。结合式(15)至式(17),选出最优解可得到优化后各物料的最优配送批量和配送间隔期,如表2所示。
对比分析优化前后各物料总配送成本、车辆空置率和物料配送间隔期变化。如表3所示,优化前各物料配送批量缺乏经济性,配送总成本为6 760.8元,小车空置率为24.3%。优化后物料配送总成本为5 321.4元,相比优化前减少1 439.4元,减少了21.3%。平均车辆空置率与优化前相比有所上升,由24.3%增加至36.9%。平均物料配送间隔期由113.5min缩短为86.9min,缩短了23.4%,实现了物料配送的优化。本算例说明该优化模型确定的物料配送期量,减少了配送时间间隔,避免物料大批量配送和线边物料库存过多,降低配送总成本的同时兼顾AGV小车空置率,验证了该模型和算法的有效性及可行性。
5 结束语
针对传统物料配送难以满足农机混流生产的问题,考虑混流生产物料配送的复杂性,以配送总成本和AGV小车空置率为优化目标,建立了符合生产需要的物料配送期量优化模型。并设计改进了多目标灰狼优化算法,提高了算法的全局寻优能力及其收敛速度,求解了物料最优配送批量。实例验证了多目标物料配送期量优化模型和算法能更好适应农机混流生产的特性,具有良好的有效性和可行性。
参考文献:
[1] 张艳姣,吕锋,杨晓英. 面向农机制造的缓冲件库存控制策略研究[J]. 制造业自动化,2019,41(9):46-50.
[2] 马艳丽,秦钦,刘进平. 考虑成本最优的物料配送方式组合优化模型[J]. 哈尔滨工业大学学报,2022,54(3):48-56.
[3] 王昀睿,赵旭雯,等. 基于混流生产模式的装配车间物料配送路径规划方法[J]. 现代制造工程,2021(7):105-116.
[4] 胡小建,陈茹梦. 面向数字化车间液压元件的物料配送研究[J]. 合肥工业大学学报(自然科学版),2020,43(3):419-424. [5] 杨晓英,王金宇. 面向智能制造混流生产的供应链物流协同策略[J]. 计算机集成制造系统,2020,26(10):2877-2888.
[6] 葛妍娇,郭宇,等. 基于智能感知网的物料配送动态优化方法[J]. 计算机工程与应用,2019,55(22):212-218,230.
[7] 王金宇,杨晓英. 基于JIS-VMI的供应商直供线边动态物料配送期量优化[J]. 系统科学学报,2021,29(4):94-100.
[8] 张世文,袁逸萍,等. 基于实时定位的离散制造车间物料配送方法研究[J]. 机械设计与制造,2020(11):18-20,25.
[9] WANG Y, JIANG Z, WU Y. Model construction of material distribution system based on digital twin[J]. The International Journal of Advanced Manufacturing Technology, 2022,121(7):4485-4501.
[10] MULLER J. Approximative solutions to the bicriterion vehicle routing problem with windows[J]. European Journal of Operation Research, 2010,202(1):223-231.
[11] MIRJALILI S, SAREMI S, MIRJALILI S M, et al. Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization[J]. Expert Systems with Applications, 2015,47:106-119.
[12] STORN R. Differential evolution-A simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997,11(4):341-343.

