融合小波分析和时间序列模型的大跨径桥梁损伤识别技术研究

作者简介：李金儒（1990—），工程师，主要从事道路与桥梁技术研究和施工管理工作。

为了及时识别桥梁结构损伤，提高桥梁工程安全性，文章提出一种融合小波分析和时间序列模型的大跨径桥梁损伤识别技术。研究通过小波分析从监测信号中提取出与损伤相关的特征，利用时间序列模型对这些特征进行分析和预测，以实现对桥梁损伤的识别和诊断。结果表明：次边跨、高边跨、1/4跨、跨中、3/4跨和低边跨测点位置的损伤识别指标的值分别为0.999 8、0.999 4、1.099 8、1.000 0、0.999 8、0.999 9。其中，监测部位挠度值损伤识别指标的值处于95%置信区间内。在延迟11阶后，主梁跨中偏自相关系数仍在2倍标准差范围内。11阶后的偏自相关系数为0，即偏自相关系数会在11阶后截尾。该改进的方法可以提高损伤识别的准确性和可靠性，实现对大跨径桥梁损伤的早期发现和及时修复。

大跨径桥梁；损伤识别；小波分析；时间序列；AR模型

U445.7A361284

0 引言

随着交通基础设施建设的快速发展，大跨径桥梁在城市交通、物流运输等领域的地位日益重要。然而，由于各种因素的影响，桥梁可能会遭受损伤，严重时甚至可能导致垮塌［1］。桥梁作为交通基础设施的重要组成部分，其结构和安全性对经济发展和民生有着重要影响。因此，对大跨径桥梁的损伤识别技术进行研究，以实现对损伤的早期发现和及时修复，对于保障公众安全和促进经济发展具有重要意义。大跨径桥梁损伤识别技术主要依赖于对桥梁各种物理参数的监测和分析，物理参数包括桥梁的挠度、应变、振动等［2］。目前主流的损伤识别方法包括以信号处理、模型角度的方法等，以信号处理为基础的方法主要是利用小波分析等技术对监测数据进行处理，以提取损伤特征。而以模型为基础的方法，则是通过建立桥梁健康监测的数学模型，对损伤进行诊断［3］。因此，为了及时识别桥梁结构损伤，加强桥梁工程安全性，研究结合小波分析和时间序列模型对采集信号完成降噪处理，分析大跨径桥梁敏感性、损伤程度和抗干扰性。

[HS（3*1]1 融合小波分析和时间序列模型的大跨径桥梁损伤识别技术

1.1 基于小波分析的大跨径桥梁实测挠度数据降噪处理

小波分析是一种强大的数学工具，能够在不同尺度下对信号进行分解和分析。在桥梁损伤识别领域，小波分析可以从监测到的信号中提取出与损伤相关的特征。还可以将监测信号分解为不同的频率成分，并通过对这些成分进行分析，提取出与损伤相关的特征，这些特征可以包括损伤的位置、大小、类型等［4］。傅里叶变换是一种分析信号的方法，它可分析信号的成分，也可用这些成分合成信号。设时域信号函数ft任意可积，ft是t的周期函数，时域信号函数ft的傅里叶变换，如式（1）所示：

时域信号函数ft的傅里叶逆变换如式（2）所示：

傅里叶变换的局限性在于需要利用信号的全部时域信息，时域变化带动频域特征的变化，缺少时域定位功能导致无法同时在时频域内分析信号。针对此问题，短时傅里叶变换可以确定时变信号其局部区域正弦波的频率与相位。其选择一个时频局部化的窗函数，假定分析窗函数gt在一个短时间间隔内是平稳状态，移动窗函数，使ft、gt在不同的有限时间宽度内是平稳信号，从而计算出各个不同时刻的功率谱。短时傅里叶变换时频分析能力强，窗函数具有灵活性，计算效率更快。但时间和频率的分辨率存在矛盾性，选择窗函数较难，信号长度有所限制，过长过短均会导致结果误差。连续小波变换是将小波函数在某个尺度下与待处理信号卷积，利用连续小波变换可以从频率表征中构建良好的时频局域化。本质上，连续小波也就是一组可控制通带范围的多尺度滤波器。连续小波变换会产生大量冗余数据，而离散小波变换为解决冗余可以生成紧凑数据。Mallat在Meyer提出一组构成标准化正交基的小波基础上，从函数角度上提出了多分辨分析的概念，结合所有的正交小波的构造方法，提出了Mallat算法，即从空间概念上形象说明小波的多分辨率特性，随着尺度由大到小变化，在各尺度上可以由粗到细的观察图像的不同特征的一种算法［5］。假设正交多分辨分析的尺度函数θx，如式（3）所示。

研究红岩村大桥位于重庆市，线路北起红石路隧道，上跨嘉陵江水道，南至红岩村隧道。大桥全长732.8 m，主跨375 m，上层桥面为双向六车道城市快速路，设计速度为80 km/h，下层为双线城市交通轨道及双向四车道城市支路，设计速度分别为100 km/h及40 km/h。桥梁模型示意，如图1所示。

图1中，红岩村大桥分别由主桥、两座桥塔、斜拉索、两岸引桥等组成，主桥路段呈西北至东南方向布置，设计荷载等级为城市A级。主梁采用双主桁等高度连续钢桁梁，主桁为两片主桁的纯滑轮桁架，桁间距为28.2 m。P3为高塔，总高度为202 m，布置28对斜拉索，P4桥塔为低塔，总高度为150.75 m，布置14对斜拉索，采用门式框架钢筋混凝土结构。1、2、3、4、5均为有限元模型中大跨径桥梁的主跨测点，为了测量加速度响应，在测点均设置加速度传感器，在跨中位置3施加均值为0、方差为1的高斯白噪声作为外激励荷载［6］。

1.2 基于时间序列模型的大跨径桥梁损伤识别指标

在小波分析基础上，研究利用Mallat算法对采集数据完成分解、降噪，去除信号中的趋势项，建立以AR（Auto-regressive）模型残差损伤识别指标。AR模型原理是对于某一任意时刻t所对应值Xt是前面p个时刻对应观测值的线性估计，表示现在与以前观测值的关系。随机序列Xt，如式（7）所示。

该平稳序列性质延续弱平稳序列，即Varrt=Varrt-1，其中ACF值可以用来描述序列的自相关性，并且还需要设置置信区间，在公式中由alpha来代表，其中alpha=0.05表示为有5%的可能性会发生误判。研究成功进行损伤识别的决定因素，在于通过拟合采集得到的时间序列Xt，得到正确的时间序列模型。在构建一个时间序列建模之前，首先要获得该组织的输出信号，进而构建一个观察的时间序列Xt，之后对其进行测试和预处理，最终获得满足平稳、正态、零均值等条件的时间序列。时间序列建模的流程为数据的采集、检验和预处理、模型参数φi估计、模型的定阶。由于建模中，要求时间序列Xt离散，而物理系统绝大部分的输出为连续信号，故离散化采集连续信号。研究选取适合的采集频率fx及样本长度L，从而获得连续信号中含有的有效信息［7-8］。离散化采集连续信号构成Xt的频谱可能会在频域产生变化，为了避免采样信号频谱发生变化，而出现高、低频成分发生混淆现象，fx需要达到fx≥2.5fmax，fmax为连续信号中适合频率要素的最大频率。L主要与信号发生于频域的能量泄漏效应，以及谐波的分辨力由不同频率主导的问题有关。加窗即是为了减少频谱泄露而对每个时间窗口进行一些处理，使其更加平滑。加窗会产生能量泄露，通常是通过使用不同类型的窗函数来解决。窗函数的宽度L用来破解不同频率分辨力的问题。因此，为确保能够分辨出信号中适合的谐波要素，样本长度L应满足，如式（11）所示。

式中：Δfmin表示在该讯号中适用于该讯号之最少频率。AR模型建立正确与适用是时间序列模型能否成功使用的关键，而在AR模型建立过程中，最重要的就是估计模型参数φi，其次为检验模型是否适用。当估计参数φi的方式不够准确时，就不能获得成功的结果。研究对模型的定阶法为结合AIC准则和FPE准则，AIC信息准则（Akaike information criterion）是衡量统计模型拟合优良性（Goodness of fit）的一种标准［9］。其建立在熵的概念基础上，可以权衡所估计模型的复杂度和此模型拟合数据的优良性，表达如式（12）所示：

式中：e2kT——惩罚因子。最终预报误差准则（Final Prediction Error Criterian，FPE），表达如式（13）所示：

建立时间序列模型并进行损伤识别，损伤识别指标α为未知状态的AR模型残差方差和未损伤状态的AR模型残差方差之比，如式（14）所示：

式中：varμivarei为测点处于未知或受损的情况下的一组模式对应残余值的方差，为测点处于无损伤的情况下的一组模式残余值的方差［10］。以某测点的损伤识别指标α和前一测点的损伤识别指标α之差的绝对值与前一测点的损伤识别指标α之比作为损伤敏感指标β，如式（15）所示。

式中：i——测量点的个数。

[HS（3*4]2 融合小波分析和时间序列模型的大跨径桥梁损伤识别技术性能分析

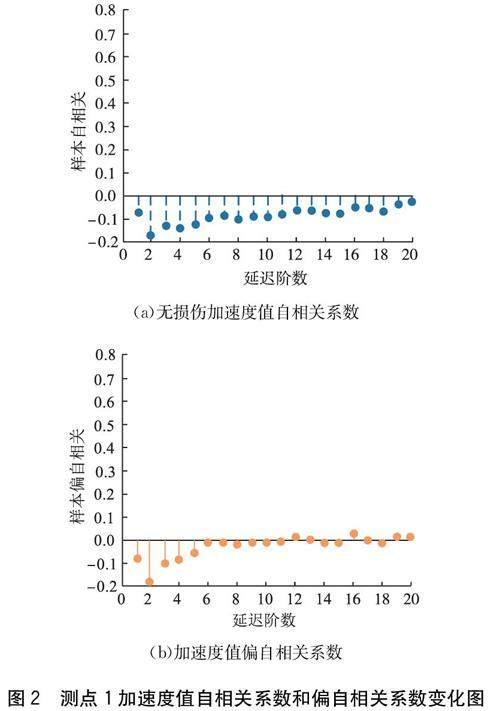
研究采集了五个测点各100 s的加速度时程数据，采样频率500 Hz，并选取了5 000个测点加速度数据进行数据分析。对测点1、2、3、4、5的无损伤加速度建立AR模型，对各处无损伤加速度值进行白噪声检验和平稳性检验，然后将各测点的无损伤加速度值平稳化后，计算测点1无损伤加速度值的自相关系数和偏自相关系数，如图2所示。

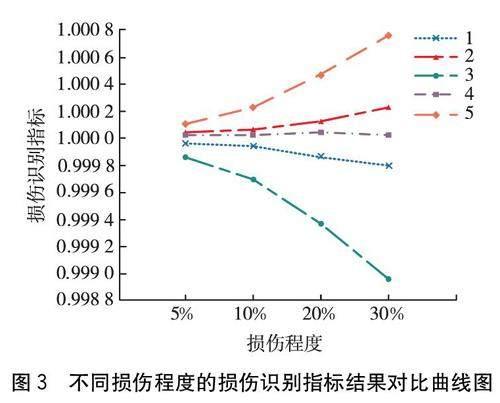
图2（a）中，测点1的加速度自相关系数衰减速度缓慢，序列以指数率单调递减，自相关系数存在拖尾现象。图2（b）中，在5阶之后测点1的加速度偏自相关系数明显大于2倍标准差范围，因此在5阶之后测点1加速度的偏自相关系数为0，即在5阶之后测点1加速度的偏自相关系数呈现截尾现象。根据AR模型的统计特性，测点1加速度值是AR（5）模型。为了模拟损伤，研究通过改变损伤区域单元的弹性模量来标识损伤区域，并设置了5%、10%、20%和30%四种不同程度的损伤情况。测点1～5不同损伤程度的损伤识别指标结果对比，如图3所示。

图3中，随着损伤程度增加，测点2、5损伤识别指标曲线均有上升趋势，其余测点损伤识别指标曲线均有不同程度的下降，但5个测点在不同损伤程度的损伤识别指标值相差较小，所以难以判断损伤位置。研究1～5测点之间在不同程度的损伤敏感指标β，如图4所示。

图4中，4个测点区间中，损伤程度为30%的β数值均为最高，损伤程度为5%的β数值均为最低。在测点区间［2，3］中，5%、10%、20%和30% 4种损伤程度的β数值均为最高，分别为0.019%、0.038%、0.078%和0.127%。测点区间［3，4］的4种损伤程度β数值仅次于测点区间［2，3］，因此设置损伤区域为测点3。研究对采集到的数据降噪之后进行标准化处理，以便检测数据达到时间序列建模要求。研究2021年10月被降噪后的数据，主梁跨中挠度自相关系数和偏相关系数对比结果，如图5所示。

图5（a）中，在延迟11阶后，偏自相关系数仍在2倍标准差范围内。因此，11阶后的偏自相关系数为0，即偏自相关系数会在11阶后截尾。图5（b）中，主梁跨中2021年10月挠度值的自相关系数的衰减速度缓慢，说明自相关系数存在拖尾现象。由于AR模型的统计特性，初步判定该数据是AR（11）模型。在主跨的1/4跨、跨中、3/4跨以及辅助跨的跨中处设置测点，将各测点经过小波分析降噪后的数据建立了时间序列模型，并计算损伤识别指标α，各测点具体计算结果，如图6所示。

图6中，次边跨、高边跨、1/4跨、跨中、3/4跨和低边跨测点位置的α分别为0.999 8、0.999 4、1.099 8、1.000 0、0.999 8、0.999 9。不同测点的α相差不大，大约为1，因此斜拉桥梁处于未损伤或微小损伤状态。

3 结语

为了避免出现桥梁工程事故和经济损失，研究利用小波分析对采集数据完成分解、降噪，去除信号中的趋势项。完成数据预处理之后，研究通过AR模型残差损伤识别指标，分析大跨径桥梁敏感性和抗干扰性，对其结构进行损伤识别。结果表明，测点1的加速度自相关系数衰减速度缓慢，序列以指数率单调递减，自相关系数呈现拖尾现象。在5阶之后测点1的加速度偏自相关系数明显大于2倍标准差范围，因此在5阶之后测点1加速度的偏自相关系数为0，即在5阶之后测点1加速度的偏自相关系数呈现截尾现象。4个测点区间损伤程度为30%的β数值均为最高，损伤程度为5%的β数值均为最低。在测点区间［2，3］中，5%、10%、20%和30% 4种损伤程度的β数值均为最高，分别为0.019%、0.038%、0.078%和0.127%。测点区间［3，4］的4种损伤程度β数值仅次于测点区间［2，3］，因此设置损伤区域为测点3。次边跨、高边跨、1/4跨、跨中、3/4跨和低边跨测点位置的α分别为0.999 8、0.999 4、1.099 8、1.000 0、0.999 8、0.999 9。不同测点的α相差不大，大约为1，因此斜拉桥梁处于未损伤或微小损伤状态。该数值处于95%置信区间，即桥梁处于未损伤或微小损伤状态。但时间有限未扩大范围采集数据，未来可以在此改进以适应更复杂和更广泛桥梁类型和环境条件。

参考文献

［1］巫生平，蒋国平.基于位移平均曲率差的桥梁结构损伤识别方法研究［J］.振动与冲击，2023，42（10）：240-250.

［2］程东风，王万庆，张秀成，等.基于遗传算法的两阶段铁路桥梁结构损伤识别［J］.科学技术与工程，2023，23（16）：7 096-7 103.

［3］戴乐诚，俞阿龙，周星宇，等.改进粒子群算法在桥梁结构损伤识别传感器优化布设中的应用［J］.现代电子技术，2019，42（7）：133-138，152.

［4］包龙生，曹 悦，赵 宁，等. BP神经网络和曲率模态理论在桥梁损伤识别中的应用［J］.沈阳建筑大学学报（自然科学版），2021，37（2）：296-302.

［5］安 宁，和海芳，马 瑞，等. 基于车-桥响应连续小波变换的桥梁无模型损伤识别方法［J］.公路交通科技，2022，39（8）：25-31.

［6］杨婷婷，李 岩，林雪琦. 基于车辆制动激励和小波包能量分析的连续梁桥基础冲刷识别方法［J］.中国公路学报，2021，34（4）：51-60.

［7］黄 淇，郭惠勇.基于GARCH-M模型的非线性损伤识别和实验研究［J］.振动.测试与诊断，2022，42（6）：1 092-1 098，1 241-1 242.

［8］Oskoui E A，Taylor T，Ansari F. Method and monitoring approach for distributed detection of damage in multi-span continuous bridges［J］.Engineering Structures，2019，189（6）：385-395.

［9］孔 烜，李思琪，韩振勇，等.适用于中小跨径桥梁频率识别的移动检测车辆参数研究［J］.湖南大学学报：自然科学版，2023，50（7）：12-22.

［10］ZHANG，Yumei，BAI，Shulin，LU，& Gang，et al. Kernel Estimation of Truncated Volterra Filter Model Based on DFP Technique and Its Application to Chaotic Time Series Prediction［J］.Chinese Journal of Electronics，2019，28（1）：131-139.