基于博弈论和BP神经网络的桥梁风险预测模型

黄伟 袁光杰

摘要：文章以桥梁施工风险的定义为主线，分析了常用桥梁风险评估方法的特点并取其长处，同时引入了熵理论和博弈论思想，提出了一种新的风险评估方法——基于博弈论和BP神经网络的风险预测模型，并以庞纳子大桥为工程实例进行应用分析。研究可知：该模型以减少主观成分为原则，通过提高评价指标的准确度、全面性和科学性进而获得可靠的风险预测值；该桥高墩施工风险值为0.348，判定该项目风险较低，在可接受范围内；主要风险因素依次为墩身垂直度、风荷载、日照温差、混凝土强度等；建议在施工过程中对其墩身垂直度进行风险监控。

关键词：桥梁风险；博弈论；BP神经网络；风险评估方法；风险预测

中图分类号：U442.3+9  文献标识码：A

文章编号：1673-4874（2024）04-0173-04

0 引言

随着内陆平原地区交通网日趋完善，公路桥梁建设的重心逐步向西部山区延伸［1］。这些桥梁往往处于风力大、温湿差大等复杂环境，施工过程面临的风险较大，如何识别和应对施工过程中可能发生的风险问题显得愈加突出。通过风险评估来解决前述问题成为近年来的一个新思路。

然而，国内外学者关于桥梁风险分析理论的研究和应用相对较少，现有常用风险评估方法也存在一定的不足。因此，本文以桥梁施工风险的定义为主线，分析常用桥梁风险评估方法的特点并取其长处，同时引入了熵理论和博弈论思想，提出一种新的风险预测模型，并以庞纳子大桥为工程实例进行应用，为指导工程风险评价提供高效准确的方法。

1 桥梁施工风险的定义及度量

在桥梁施工过程中，对相关利益团体的某种既定目标造成影响的不确定事态［2］，称为桥梁施工的风险事态，简称桥梁施工风险。其一般的数学表达如式（1）所示，即风险值R是关于风险事件发生的概率p、风险后果c、目标利益发生的概率q和目标利益b的某种函数关系式，该式也呈现了风险与收益之间的博弈关系：

R=f（p，c，q，b）（1）

式中：R——风险的数值度量；

p——风险事件发生的概率；

c——风险事件引起的后果（损失）；

q——目标利益发生的概率；

b——目标利益。

其中，在并协原理下，风险事件发生的概率p与目标利益发生的概率q呈互补关系，见式（2）；当收益可忽略或难以衡量时［3］，可将式（1）简化为如式（3）所示，即由风险事件发生的概率p和风险后果c来综合表达风险值R。

p+q=1（2）

R=f（p，c）（3）

2 常用桥梁风险评估方法分析

常用的桥梁风险评估方法有层次分析法、模糊综合评价法、BP神经网络分析法。

2.1 层次分析法

层次分析法（AHP）是将与决策相关的因素分解为目标、准则、指标等层次，对复杂决策问题的本质、影响因素及其内在关系等进行深入分析，利用较少的定量信息使决策的思维过程数学化，从而为复杂问题提供简便的决策方法，适用于决策结果难以量化的场合。由层次分析法可计算风险因素的相对权重或发生概率，见式（4），但定量数据较少，定性成分多，其计算结果不易令人信服。

ω=f（p）f（p，c）（4）

2.2 模糊综合评价法

模糊综合评价法基于模糊数学将定性评价转化为定量评价，适用于各种非确定性问题的解决。由模糊综合评价法可计算风险值，见式（5）、式（6），但评价指标权重向量ω的初始判断矩阵、评价指标关系矩阵S的构建很大程度上受决策者主观意向的影响，双重主观判断使得评价结果向量B和风险值R的准确性有待商榷。

B=ω·S（5）

R=B～·MT（6）

式中：B——评价结果向量；

ω——评价指标权重向量；

S——评价指标关系矩阵；

B～——归一化后的评价结果向量；

MT——评价等级的风险值向量。

2.3 BP神经网络分析法

BP神经网络是指一种基于逆传播算法的多层前馈网络，其本质为一个输入向量x[DD（-*9]→[DD）]到输出向量y[DD（-*9]→[DD）]的函数，（见式7）［4］。BP网络以自学习、自适应、非线性映射等优点在函数逼近等领域应用甚广，其在运用中常与层次分析法相结合，将由层次分析法解得的各风险指标权重作为网络中目标项目的变量，同时使自变量涵盖了层次分析法准确度不高的特性，进而影响了网络的预测值。

y→=f（x→）（7）

3 基于博弈论和BP神经网络的风险预测模型

基于上述对常用桥梁风险评估方法的分析，引入熵理论和博弈论思想，提出一种新的风险预测模型。

3.1 熵权法

在信息论中，熵为系统无序程度的度量。

熵权法是基于工程项目历史或现有客观数据的考察利用，有较强的数理依据，其基本思路是根据指标的变异程度来确定客观权重。对于某项指标，其信息熵值越小，表明该指标的离散程度越大，在综合评价的权重越大，反之则相反。若某项指标的值均相等，则该指标在综合评价中不起作用。因此，熵权本身并不表示指标权重，而表示在该指标下对评价对象的区分度。

3.2 博弈论集化模型

博弈论集化模型的核心思想是在不同赋权方法所获取的指标权重之间寻求一致或妥协，极小化可能的权重与各基本权重之间的偏差［5］，提高指标赋权的科学性。具体实现过程如下：

运用AHP、熵权法对评价指标进行求解，可得指标权重集如式（8）所示，记基本权重向量ωl的任意线性组合如式（9）所示。运用博弈论集化模型在前述两种不同权重之间进行优化，由优化目标（ω与ωl的离差极小化）可推导出决策模型如式（10）所示。

ωl=（ωl1，ωl2，…，ωln） l=1，2（8）

ω=∑2l=1αlωl（9）

式中：αl——线性组合系数。

min‖∑2i=1αiωTi-ωTl‖（10）

根据矩阵的微分性质，上述决策模型的最优化一阶导数条件［6］如式（11）所示，对应式（12）的线性方程组。

∑i=1αiωlωTi=ωlωTl（11）

ω1·ωT1ω1·ωT2ω2·ωT1ω2·ωT2α1α=ω1·ωT1ω2·ωT2（12）

解式（11）并按式（13）进行归一化处理，最终可求得综合指标权重如式（14）所示。

αl=αl∑2l=1αl（13）

ω=∑2l=1αlωl（14）

3.3 基于博弈论和BP神经网络的风险预测模型

在定性定量综合风险评估中，指标权重的确定尤为重要。

为得到更准确、更全面的工程指标权重，以减少主观成分为原则，在仅考虑“风险事件发生的概率p”这一判断准则下，立足于博弈论并以Nash均衡为协调目标［5］对AHP权重、熵权进行优化，可根据实际相似工程评价指标的变异程度，通过熵权对AHP指标权重进行修正，提高指标的准确度；同时，避免了单一赋权方法的片面性，获得兼顾专家意见和项目客观情况的综合权重，提高了指标的全面性、科学性。

联合BP神经网络能学习和存贮大量类似项目输入-输出（风险事件发生的概率p-风险值R）模式映射关系的特性，合理有效地解决了非正态分布、非线性的风险预测问题［7］。

基于博弈论和BP神经网络的风险预测模型技术路线如图1所示。该模型适用于决策系统难以定量的情形。

4 工程应用

4.1 工程概况

G580线和田至康西瓦公路工程庞纳子大桥位于新疆和田地区，主桥桥跨布置为100 m+100 m的预应力混凝土连续刚构桥（下页图2），T构采用悬臂施工，最大悬臂长度为93 m，桥宽9 m，主墩为空心薄壁墩（下页图3），高161 m，其墩高位居国内同类型桥梁中第6位，采用爬模施工。

由于本桥结构体系复杂，同时桥址区位于峡谷风口地带、地震基本烈度为Ⅷ度的高海拔区域（桥面海拔约2 460 m），加之高温差、高紫外线、干旱等气候条件的影响，使得施工过程中不确定因素较多，施工难度较大。针对该桥建设条件的特殊性，应加强对施工技术和方案的研究［3］，开展施工过程风险评估工作。

4.2 实桥应用

由于超高墩连续刚构桥主墩施工控制参数较主梁少，没有预应力束张拉控制等参数，且墩身截面较主梁尺寸较小，不利于不平衡荷载等工况的模拟，部分主墩施工风险指标难以量化。因此，采用基于博弈论和BP神经网络的风险预测模型对该桥高墩施工风险进行预测。

通过典型案例分析并结合工程实际，识别高墩施工风险因素进而建立具有层次结构的风险预测指标体系，具体如图4、表1所示。

基于上述风险预测指标体系，分别运用AHP、熵权法对各层评价指标进行求解。由于篇幅限制，此处直接给出各评价指标的权重ω1、ω2，如式（15）、式（16）所示。

ω1=0.107，0.088，0.066，0.396，0.134，0.111，0.052，0.046（15）

ω2=0.110，0.053，0.055，0.397，0.170，0.111，0.057，0.047（16）

由博弈权重集化式（10）～（14），求出该项目施工风险评价指标的综合权向量ω，如式（17）所示。

ω=0.108，0.077，0.063，0.396，0.145，0.111，0.053，0.046（17）

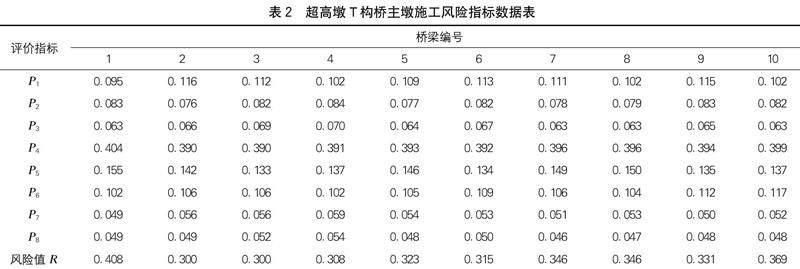
利用Matlab软件创建该指标体系下的BP神经网络。为确保网络（函数）的准确性，选取10座经项目验证的超高墩T构桥（如赫章特大桥等）作为网络的训练和测试样本。随机抽取9组数据作为训练集，1组数据作为测试集，具体数据如下页表2所示。

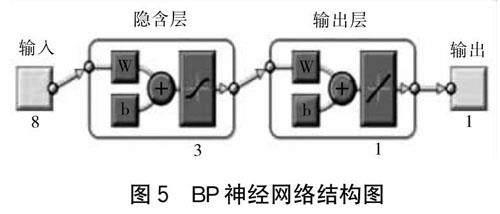
将评价指标Pi作为输入层神经元，将风险值R作为输入层神经元，采用试凑法确定网络收敛最快、误差最小时对应的隐藏层节点数为3［7］，其结构如下页图5所示。

然后将所有样本代入后检验得，10组数据平均相对误差为0.489%，最大误差为1.57%，故该网络拟合较好，可用于超高墩T构桥主墩施工风险预测。

将庞纳子大桥高墩施工风险评价指标的综合权向量ω输入上述网络，得到风险预测值为0.348，由表3可判定该项目风险较低，在可接受范围内。

根据综合权向量ω及表2中风险指标Pi-风险值R之间的映射关系可知，该项目施工主要风险因素依次为：墩身垂直度、风荷载、日照温差、混凝土强度等。其中，风荷载、日照温差均会影响高墩的垂直度，因此建议在该项目施工过程中对其墩身垂直度进行风险监控。

5 结语

（1）基于博弈论和BP神经网络的桥梁风险预测模型以减少主观成分为原则，通过提高评价指标的准确度、全面性和科学性进而获得可靠的风险预测值。

（2）由预测模型求得庞纳子大桥高墩施工风险值为0.348，判定该项目风险较低，在可接受范围内。

（3）该项目施工主要风险因素依次为：墩身垂直度、风荷载、日照温差、混凝土强度等。

（4）建议在该项目施工过程中对其墩身垂直度进行风险监控。

参考文献

［1］袁光杰.复杂环境下超高墩T构桥施工过程风险分析与应对措施研究［D］.重庆：重庆交通大学，2020.

［2］姜越川.连续刚构桥施工风险评估研究［J］.中外建筑，2011（2）：77-78.

［3］李凌俊.超高墩连续刚构桥施工期内风险评估研究［D］.重庆：重庆交通大学，2012.

［4］金 晶，李宗昊，朱 亮，等.BP神经网络在铁路建设风险评估中的应用［J］.铁道工程学报，2019，36（3）：103-109.

［5］吴小萍，储诚诚，李月光，等.博弈论在高速公路施工期环境影响评价中的应用［J］.郑州大学学报（工学版），2012，33（6）：36-40.

［6］苏观南，付修庆，刘天祥.改进的博弈论综合权重在大坝安全综合评价中的应用［J］.中国农村水利水电，2014（11）：82-85.

［7］王飞球，黄健陵，符 竞，等.基于BP神经网络的跨既有线高速铁路桥梁施工安全风险评估［J］.铁道科学与工程学报，2019，16（5）：1 129-1 136.

［8］方 鸿.跨铁路高墩连续刚构桥稳定性研究及风险分析［D］.长沙：长沙理工大学，2012.

［9］纳启财.高原地区环境及养护条件对混凝土性能的影响［J］.混凝土与水泥制品，2016（1）：10-13.

［10］张谢东，郭俊峰，余建宜，等.山区高墩大跨桥梁施工过程中的风险识别［J］.桥梁建设，2008（6）：80-83.

［11］虞 辉，李利军，张 溪.山区高墩连续刚构桥安全风险评估研究［J］.现代交通技术，2012，9（1）：29-32.

作者简介：黄 伟（1988—），研究方向：桥梁风险评估、桥梁健康监测。