梯级枢纽联合调度下通航水位的确定分析

唐继彬 黄伟荣 胡颖 郑景琦 汪路瑶

摘要：文章通过建立桂江航道京南枢纽至旺村枢纽长河段二维水流数学模型，基于两枢纽调度规则和实际调度情况，分析不同水情下研究河段沿程水位特征，并确定了采用枢纽联合运行各组水位下包络线作为该河段的设计最低通航水位，重现期10年一遇的洪水位作为该河段的设计最高通航水位，为该航段整治工程提供了技术支撑。研究成果可为类似梯级枢纽联合调度下航道设计水位的确定提供技术参考。

关键词：桂江航道；枢纽；梯级；联合调度；通航水位

中图分类号：U641.7+3   文献标识码：A

文章编号：1673-487（2024）04-0213-04

0 引言

航道通航水位是水域交通规划和工程设计中的重要参数［1-2］，一般包括设计最低通航水位和设计最高通航水位［3］。其中，最低通航水位直接关系着船舶航行的通航保证率［2，4-6］，最高通航水位主要关系到通航建筑物或跨河建筑物的通过能力等［7-12］，其合理确定直接影响船舶的安全通行和水上交通系统的运行效率。科学且综合地制定通航水位，可以为航道规划和工程设计提供坚实的基础，促进水域交通的发展和优化。

两枢纽间航道设计通航水位的确定是航道设计的关键。本文的研究河段位于桂江航道京南枢纽和旺村枢纽两梯级间。区别于受径流控制的天然河道，研究河段沿程水位受两枢纽联合运行影响，具体表现为受到上游京南枢纽的出库流量与下游旺村枢纽坝上运行水位共同控制，沿程水位变化复杂，水位流量关系并非单调的变化趋势。

本文通过建立桂江京南枢纽至旺村枢纽长河段二维水流数学模型，深入剖析两枢纽调度规则和实际调度情况，分析研究河段在不同水情下的沿程水位分布特征，并确定研究河段的沿程设计通航水位。研究成果可为本河段航道整治提供技术支撑，也为类似梯级枢纽联合调度下航道设计通航水位的确定提供技术参考。

本文高程数据如无特殊说明为1985国家高程系统。

1 研究河段概况

桂江位于广西壮族自治区东北部，作为珠江水系西江干流的主要支流之一，是西江黄金水道的重要组成部分，是沟通桂江流域桂林、贺州、梧州与西江干线的重要航运通道，也是《国家综合立体交通网规划纲要（2021—2035）》高等级航道“四纵”之一的汉—湘—桂通道的重要组成航段。目前桂江已建成巴江口、昭平、下福、金牛坪、京南和旺村共计6个梯级，基本实现渠化，为航道提档升级提供了有利条件。

研究河段位于桂江京南枢纽-旺村枢纽区间，河段全长约42.3 km。桂江京南枢纽是桂江干流（平乐以下河段）的第5个梯级，位于桂江下游的苍梧县京南镇，距梧州市68 km，以发电为主，兼有航运、灌溉、水产养殖、旅游等综合利用效益。京南梯级工程于1993年9月动工，1997年3月一期工程完成，1997年6月28日第一台机组发电。桂江旺村枢纽是桂江干流（平乐以下河段）的第6个梯级，也是桂江开发的最末一个梯级电站，位于桂江下游梧州市长洲区倒水镇平浪村附近，距桂江河口24.3 km，是一座以发电为主，结合航运，兼顾其他综合利用的水电枢纽工程。旺村梯级工程于2006年12月18日正式开工建设，2011年12月31日船闸通航。

在本次桂江航道扩能升级工程中，研究河段按内河Ⅲ级航道标准建设。航通航保证率95%，航道尺度为3.5 m×60 m×480 m（航道设计水深×通航宽度×最小弯曲半径）。

2 研究河段基本水情分析

2.1 水文站点水位流量关系

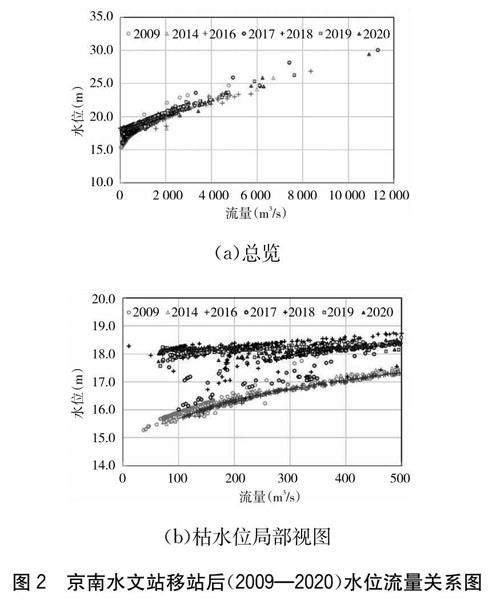
研究河段设有京南水文站，位于京南枢纽坝下，于1999年1月设立并开始观测水文观测项目。考虑旺村电站尾水影响，对水位观测不便，于2009年1月1日起，将观测水尺移至坝址下游3 km处。

根据京南水文站移站后2009—2020年间的水位流量关系（图2）可以看出，研究河段来流量一般集中在0～5 000 m3/s，2009—2014年京南水文站水位流量关系未发生显著变化，2014—2017年，旺村枢纽蓄水初期，水位逐步上升，尔后在2018—2020年水位流量关系基本未发生显著变化。可见，表明研究河段河床总体保持较为稳定的状态。

根据旺村枢纽投入运行后坝上水位流量关系可以看出（图3），旺村枢纽投入运行后蓄水初期，运行水位从12.43 m逐步抬升，至2017年蓄水期末期逐步抬升至17.13 m以上；汛期提前腾库，水位下降，＜17.13 m；遇船闸检修时水位下降至13 m以下。

2.2 旺村枢纽运行调度情况

研究河段位于京南枢纽至旺村枢纽区间，在京南水流出库流量一定的条件下，旺村枢纽坝上运行水位将直接影响着区间内的沿程水位。因此主要分析旺村枢纽坝上运行水位的运行方式。

根据《旺村电站水库调度运行规程》（Q/GGSD112.019-2017），梳理研究河段下游旺村枢纽坝上水位运行方式。

旺村枢纽坝上正常蓄水位为18.13 m，水库水位必须严格控制在正常水位以下运行。在无泄洪要求时，水库水位须高于水库最低运行死水位17.13 m。当来水量大于742.5 m3/s后，为减少上游回水淹没，通过发电或开启泄水闸提前腾库，以降低水库运行水位，水位逐步下降。当来流量大于4 700 m3/s时，机组全停，水库敞泄，河道恢复天然状态。

旺村坝上运行水位具体见表1。

2.3 旺村枢纽实际运行调度分析

鉴于缺少旺村枢纽历史入库流量资料，因此根据2014—2020年京南水文站流量资料和旺村坝上运行水位分析旺村枢纽坝上实际运行情况。

旺村枢纽于2013年投入运行，2014—2017年初蓄水期库区低水位运行，坝上运行水位在极限死水位13.65 m附近；2017年以来，除因设备检修等原因以13 m以下低水位运行外，非汛期运行水位基本能够维持在17.13～18.13 m。如图4所示。

总体上看，旺村实际运行方式基本符合调度规程的运行方式。

3 设计通航水位计算分析

与天然河道不同，两梯级间河道水位同时受上游梯级出库流量和下游梯级坝上运行水位共同控制，沿程水位与上游来流量未必呈单调变化趋势。因此，需要厘清梯级枢纽运行调度规则和实际运行情况，分析研究河段水位情况，采用二维水流数学模型计算推求可能出现的多组回水曲线［3］，方能合理确定梯级枢纽间的通航水位。

根据研究河段相关设计文件，该河段按内河Ⅲ级航道标准建设，航通航保证率95%。根据《内河通航标准》：Ⅲ级航道取为重现期20年一遇洪水位，对出现高于设计最高通航水位历时很短的山区性河流，Ⅲ级航通可采用10年。

3.1 二维水流数学模型简介

研究河段二维水流数学模型范围上起京南枢纽坝址，下至旺村枢纽，模型全长约43.2 km，模型范围如图5所示。

桂江京南枢纽至旺村枢纽段模型地形采用2022年12月至2023年2月实测的1∶2 000和局部河段1∶500水下地形资料。根据京南枢纽平面布置、河道地形特征对计算区域进行网格剖分，计算网格由无结构三角形网格单元构成。网格尺寸一般在5～30 m。整个计算网格节点约105 362个，单元208 422个。模型上游采用流量边界，下游采用水位边界控制，区间内考虑龙江支流入汇。结合京南枢纽与旺村枢纽下泄流量关系，分配龙江流量。沿程河道主槽内糙率为0.023～0.028，滩上糙率取0.028～0.040。如图5所示。

模型采用2023年1月12日实测水文资料进行了枯水验证。考虑到本河段河床总体稳定，采用2020年汛后地形及京南水文站水位对模型进行中、洪水补充验证，结果表明模型能够满足《内河航道与港口水流泥沙模拟技术规程》（JTJ/T232-98）要求，计算精度能够较好地反映研究河段的沿程水位。具体验证过程在此不一一赘述。

3.2 研究河段沿程水位变化规律

3.2.1 计算水位流量组合的确定

桂江京南枢纽至旺村枢纽段，受两级枢纽运行调度共同影响，结合枢纽调度原则，从京南枢纽最小通航流量（95%保证率流量）～最大通航流量（十年一遇洪水流量）间选取特征流量级作为本次计算条件的组合。

（1）最小通航流量：根据桂江工可报告，京南枢纽坝下最小通航流量60 m3/s（95%保证率），结合旺村枢纽运行调度规程，旺村坝上运行水位17.63 m。基于最低通航水位的不利考虑，最小通航流量条件下下游选取非汛期正常运行死水位17.13 m。

（2）最大通航流量：10年一遇洪水流量条件下，旺村枢纽敞泄，河道恢复天然状态。

总体上看，最小通航流量～旺村枢纽敞泄流量条件下，上游来流量逐步增加，而下游旺村枢纽运行水位逐步降低，沿程水位呈现出非单调变化。根据旺村枢纽运行调度规则，上游来流量大于1 600 m3/s后随着流量的增大旺村坝上水位不断下降，至4 700 m3/s电站停止发电，上游水位应≥13.63 m。因此，通过在这最低、最高通航流量级之间增设多级流量，通过不同水位流量组合条件下沿程水位的上、下包络线，以确定研究河段的最高、最低通航水位。如表2所示。

3.2.2 沿程水位分布特征

研究河段最小通航流量（95%保证率流量）～最大通航流量（十年一遇洪水流量）沿程水位计算结果如图6所示。

最小通航流量～旺村枢纽敞泄流量4 700 m3/s之间，区别于天然河道水位与来流量的单调变化，受京南枢纽下泄流量和旺村枢纽坝上水位双重控制的影响，研究河段上下游表现出相反的变化规律。随着上游京南枢纽来流量的增大，河道上游水位逐步抬升，即上游水位受来流量主导，随流量的增加呈单调递增趋势；而旺村枢纽坝上运行水位自非汛期正常运行死水位17.13 m不断下降至汛期最低运行死水位13.63 m，下游水位逐步下降，即下游水位主要受旺村坝上运行水位影响主导，尽管来流量增加，但水位仍随旺村枢纽坝上运行水位的降低而单调递减趋势。从图6可以看出，上、下游水位反向变化的转折点位于京南枢纽坝下20～30 km，且随着上游来流量的增大逐步向下游移动，表明沿程水位受流量主导的范围逐步增大。

旺村枢纽敞泄流量后（流量＞4 700 m3/s），旺村枢纽坝上水位控制取消，该河段恢复天然河道水流特性，随着流量的增大，沿程水位总体呈上升。至2年一遇洪水流量条件以上，旺村枢纽处天然水位已超过旺村坝上正常蓄水位。

3.3 设计通航水位的确定

根据上述沿程水位的变化规律，最终确定本河段的设计通航水位。

3.3.1 设计最低通航水位

根据上一节沿程水位特征，枯水期上游水位较低，而汛期旺村枢纽提前腾库，坝上运行水位下降，引起下游库区水位的降低。因此本河段设计最低通航水位并非发生于同一水情条件下。采用前文各组水位的下包络线作为本河段的设计最低通航水位。其中，0～20 km段最低通航水位对应设计最小通航流量下水位，该段也是航槽开挖主要集中的区域，鉴于水面比降趋近于0，采取平挖方式疏浚后基本不会引起本段的枯水位降落；20～30 km段为各组回水曲线的下包络线，该段航深条件良好；30～42.3 km段最低通航水位对应旺村枢纽敞泄流量下水位，此时旺村枢纽坝上运行水位降至极限死水位。

3.3.2 设计最高通航水位

根据前文沿程水位特征，洪水期当入库流量达到2年一遇洪水流量以上时，旺村枢纽处天然水位已超过坝上正常蓄水位。因此可直接采用重现期10年一遇的洪水位作为该河段的设计最高通航水位，同时也是重现期10年一遇的洪水位与多组回水曲线的上包络线。

4 结语

航道设计水位是航道规划设计的重要参数。本文针对桂江京南枢纽至旺村枢纽河段Ⅲ级航道建设中通航水位的确定，采用二维水流数学模型，计算分析了梯级枢纽间受上游流量和下游水位双控条件下沿程水位变化规律，并确定了研究河段的最低和最高通航水位。主要结论如下：

（1）2017年下游旺村枢纽运行进入蓄水期末期，受水库非恒定泄流影响，京南坝下枯水期水位流量关系散乱，而洪水期水位流量关系相对单一。水位流量关系年际总体稳定，表明研究河段河床总体保持较为稳定的状态。

（2）研究河段在旺村枢纽敞泄以前，受上游京南枢纽下泄流量和下游旺村枢纽坝上运行水位共同控制，上游水位受流量主导，随流量的增加呈单调递增趋势；下游水位主要受旺村坝上运行水位影响主导，尽管来流量增加，但水位仍随旺村枢纽坝上运行水位的降低而单调递减趋势。旺村枢纽敞泄流量后，旺村枢纽坝上水位控制取消，该河段恢复天然河道水流特性，随着流量的增大，沿程水位总体呈上升。

（3）结合京南和旺村枢纽调度规则，选取枢纽联合运行各组水位的下包络线作为该河段的设计最低通航水位，采用重现期10年一遇的洪水位作为该河段的设计最高通航水位，该航段整治工程提供技术支撑。

参考文献

［1］陈婷婷，周玉洁，赵 江，等.高坝库区和变动回水区设计最低通航水位的确定［J］.水运工程，2023（S1）：80-84.

［2］赵 燕.内河航道设计最低通航水位推求探讨［J］.中国水运，2022（10）：96-97.

［3］GB.50139-2014，内河通航标准［J］.

［4］陈 艺，黄贤智.长洲枢纽坝下3 000吨级航道设计最低通航水位可靠性研究［J］.珠江水运，2023（8）：3-5.

［5］陈婷婷，杨 涛.白鹤滩枢纽变动回水区设计最低通航水位的确定［J］.水运工程，2023（8）：134-138.

［6］吴凌波，祁永升.黄河兰州城区段航道设计通航水位分析［J］.水运工程，2023（9）：119-125.

［7］姜兴良，蔡翠苏，张德茹.株洲二线船闸设计最高通航水位的确定［J］.水运工程，2019（8）：147-150，198.

［8］徐 红.山区河流船闸设计最高通航水位确定方法的探讨［J］.中国水运（下半月），2021，21（10）：71-72.

［9］唐存本，贡炳生，张贤明.山区天然河流设计最高通航水位确定方法的探讨［J］.水运工程，2007（4）：66-69.

［10］郑 静，邓丰昌.平原河网地区内河航道设计最高通航水位取值［J］.水运工程，2017（11）：104-108.

［11］普晓刚，韦巨球，刘俊涛.西江航运干线（广西段）设计最高通航水位标准探讨［J］.水道港口，2015，36（6）：550-554.

［12］张 宇，欧阳飞，李 彪，等.长江支流河口段跨河建筑物设计最高通航水位确定方法探讨［J］.中国水运，2020（3）：21-24.

作者简介：唐继彬（1974—），工程师，主要从事航道工程管理、航道养护、航道水文等方面工作。