兼顾重心的最密堆积算法设计与实现

王红娟 李航硕 叶松扬 李儒林 肖洋洋

摘  要：该文针对目前物流行业迫切需要解决的货物存储空间利用率不高，长途货运过程中因堆叠方式不当造成货车重心不稳而存在一系列安全隐患等问题，提出一种兼顾重心的最密堆积算法。将存储空间分层，通过扫描得到货物体积、质量、是否有特殊需求等参数，综合G2LA重心算法及同、异构货物二维、三维空间最密堆积算法对货物堆积方式进行设计，以达到在保证运输过程中运输车辆重心稳定的前提下，实现仓储空间利用率最大化的目的。本算法的设计与实现，对进一步推动物流行业的发展具有重大意义。

关键词：重心问题；空间最密堆积；算法设计；仓储空间利用率；物流行业

中图分类号：TP399      文献标志码：A          文章编号：2095-2945（2024）18-0028-05

Abstract： This paper aims at the problems that the logistics industry urgently needs to solve， such as the low utilization rate of cargo storage space and a series of security hidden dangers caused by the instability of truck center of gravity caused by improper stacking mode in the process of long-distance freight transport. In this paper， a densest stacking algorithm taking into account the center of gravity is proposed. The storage space is layered， and the parameters such as cargo volume， quality and whether there are special needs are obtained by scanning， and the goods stacking mode is designed by combining the G2LA center of gravity algorithm and the two-dimensional and three-dimensional packing algorithm of the same and heterogeneous goods， so as to achieve the purpose of maximizing the utilization rate of storage space on the premise of ensuring the stability of the center of gravity of transport vehicles. The design and implementation of this algorithm is of great significance to further promote the development of the logistics industry.

Keywords： center of gravity problem; space densest packing; algorithm design; warehouse space utilization; logistics industry

在大力提倡智慧物流的背景下，物流行业发展迅速的同时也存在一些问题，如货物存储时仓储空间利用率较低，在长途运输过程中由于货物堆叠方式不当造成运输车辆重心不稳而存在一系列安全隐患等问题。为此本文提出了一种兼顾重心问题的空间最密堆积算法设计，考虑货物的质量和体积等参数，对仓储空间进行分层，综合GL2A重心算法及同、异构货物二维、三维空间最密堆积算法对货物进行合理的堆放，在保证重心稳定的前提下实现仓储空间利用率的最大化。

将同、异构货物二维[1]、三维[2]空间最密堆积算法和重心平衡约束算法[3]进行融合，首先根据货物体积、数量以及仓储空间的容量对仓储空间进行分层，在判断货物类型是相同构型或相异构型后，采用同、异构货物空间利用率最大化算法在每层对货物进行排列以保证每层的空间利用率最大化，之后考虑重心问题进行层交换、层平移、层旋转调整，对调整后的方案通过评价函数进行评价以最大程度地保证空间利用率最大化的基础上实现运输过程中重心平衡的目的。

1  空间最密堆积算法

1.1  二维排列算法

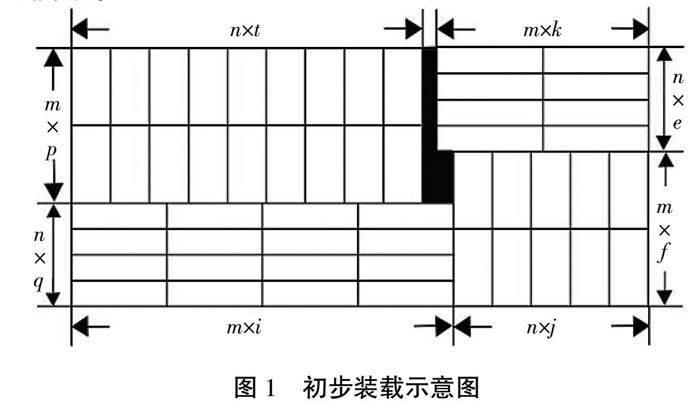
首先来讨论二维相同结构的货物排列方案[4-5]，设在给定的边长为A×B的矩形区域内（上A、下A、左B、右B），尽可能多地放入边长为m×n的小矩形，假设m≥n，通过对m、n的各种排列组合，使得在装载时对大矩形的2个边长A和B有更高的利用率，可以对m×n的小矩形进行平移和旋转对组合方案优化。如图1所示。

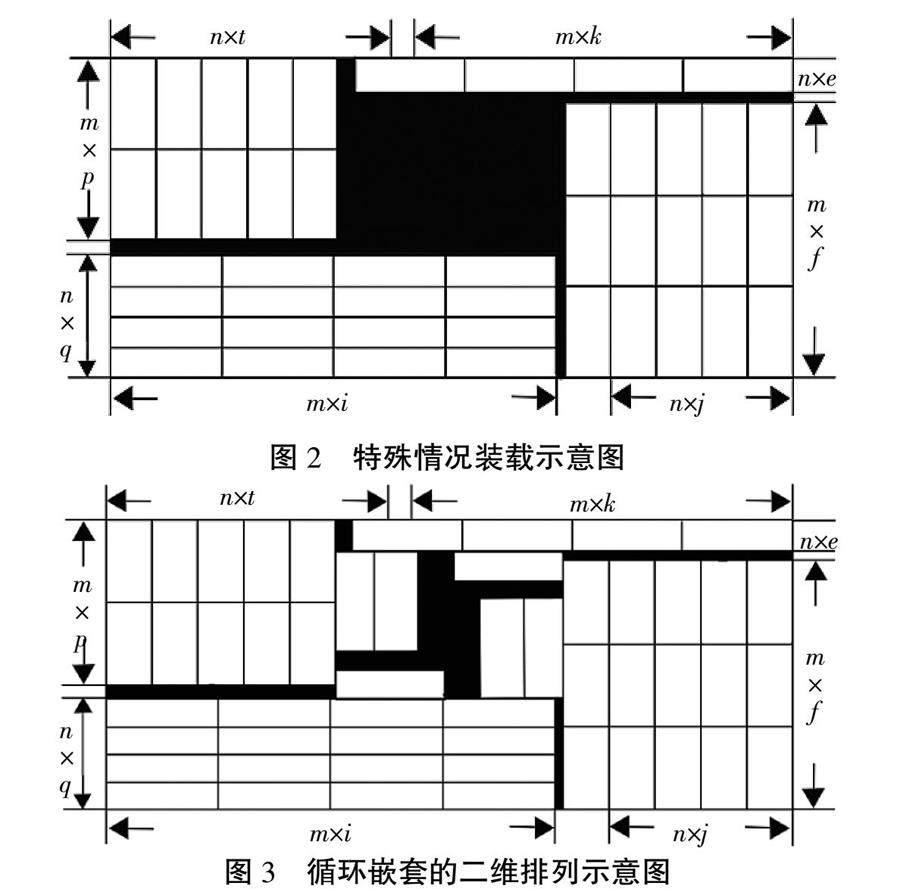
在图2中，由于算法本身是按照矩形的外侧进行排列的，故而在进行物体的空间利用排布时，可能会在中间区域形成较大的未被利用的部分，如图中x的阴影部分，此时可以将阴影部分视作一个新的矩形，再次利用本算法进行循环嵌套，直至剩余空间不足以存放货物为止。最终效果图如图3所示。

1.2  三维排列算法

鉴于在结构上完全一致的货物三维空间排布使用率问题，以上述二维货物的排布形式为基础，采取分层的方法，将空间三维立方体的长和宽的参数作为每一层的长和宽的参数，沿着本层的法向量以单个货物的参数为层高把三维空间分成不同的层，以此完成相同结构三维空间排布的初步装载布局。针对每一层的排布，就可以参考上述二维相同结构货物的排布方案，如图4所示。以选定装载空间左后下角作为坐标原点O建立空间直角坐标系，沿装载空间立方体的各棱所在直线延伸分别建立X轴、Y轴、Z轴，且装载空间的长、宽、高参数分别为P、Q、R。

由于在上述方案中采用了分层的思想，这里对分层的方法作进一步说明。在划分层时，要沿着已建立的空间坐标系的其中一条坐标轴，层的高度就是沿着划分层的轴的方向的长度，进而在指定的层进行二维排布。因为货物在三维空间中能绕自身的长宽高任一方向旋转，都可以达到平行于装载空间底面的状态，故共有6种摆放方式，其中3种分层方式如图5所示。

沿Z轴即箱体高度方向分层，二维布局矩形平面为P×Q。

沿Y轴即箱体长度方向分层，二维布局矩形平面Q×R。

沿X轴即箱体宽度方向分层，二维布局矩形平面P×R。

2  G2LA重心平衡约束的装载算法

2LA算法是解决近似立方体装载的高效算法，展示出较高的空间利用率，本文基于G2LA算法通过研究目前存在的其他较为高效的基于块装填的近似立方体装载的算法后通过4个重要环节组成的此类算法的研究模式并在此基础上进行了一定的改良，下面是对这4个重要环节进行简述。

近似立方体装载的空间约束的表达形式，不采用 G2LA 算法的 cover representation，而选择采用更有利于形成更高空间利用率的基于矩阵的空间约束表达形式。

把G2LA算法选取的多异构块装填方式变成选取简单异构装填方式，其意义是能够和混合禁忌搜索算法的编码模式相匹配。

通过尽可能缩小G2LA算法的以定义立方体的底面参考点来计算的anchor distance值来选用所提供装载空间的方式，意义是能够采用混合禁忌搜索算法的编码模式来按照物品类型的顺序来模拟装载物品。示意图如图6所示。

简单块选择算法采用G2LA算法。G2LA算法示意图如图7所示。

G2LA算法示意图参考点表示目前的搜索状态。当要装填一个物品块时，通过评价函数筛选最高效的M个物品块所筛选出的装填方式，对M个物品块中的所有筛选出的一部分装填方式，再次筛选出最高效的M个物品块所形成的装填方式，这样每一次迭代要总共筛选2M个装填方式。对这一部分装填方式，虽然存在评价函数不能准确描述剩余空间的情况但利用基于最大体积的贪婪算法可以得到一个较为完整的装填方式。所以，对一个可装填空间t和一个物品块f（b），可以采用评价函数：f（t，f）=V+k·Vs。

3改进型兼顾重心问题的异构货物空间利用率最大化算法

3.1异构算法设计

继续沿用相同结构货物装载中分层的思想，在进行相异结构货物装载时，分为底层装载和非底层装载[6-7]。

3.1.1  底层装载函数

选取相同结构货物分层步骤中的第一层作为底层，从坐标原点处开始装填，底层装载函数的步骤如下。

1）从已知参数的货物中选择体积最大的货物首先放入装载空间，紧靠x=0，y=0，z=0处，并以此作为参考。计算此时本层的剩余空间参数，并列出剩余长度、宽度及最大高度。

2）在其余货物中挑选出符合体积参数符合剩余长度、剩余宽度、最大高度的箱子，依据所求得的体积参数降序分布，选取体积最大的箱子放入装载空间，随后再次计算剩余长度、剩余宽度、最大高度、判断剩余空间是否还能够放入箱子，循环遍历，直至本层空间无法放入箱子为止（箱子可旋转）。

3）返回装载结果，本层剩余空间的长度、宽度、最大高度，集装箱的剩余空间。如图8所示。

3.1.2  非底层装载函数

底层装载完成后，随即开始进行非底层装载。同样以该层的x=0，y=0处为起点开始装填，具体装载步骤如下：

1）筛选出体积小于剩余空间的所有箱子，并根据箱子的体积大小，对所有箱子进行排序。选取体积最大的箱子首先放入装载空间，作为参考点。

2）读取参考点货物的长、宽、高参数，并将其高度参数作为当前装载层的最大高度，确定好层高后计算该层的剩余装载空间。

3）在其余货物中挑选出符合本层剩余空间参数的箱子，计算这些箱子的体积并依据体积降次排列。选取其中体积最大的箱子放入剩余空间。随后再次计算剩余长度、剩余宽度、最大高度，判断剩余空间是否还能够放入箱子，循环遍历，直至本层空间无法放入箱子为止（箱子可旋转）。

4）计算该层的剩余空间，并将本层剩余空间的长、宽、高与上一层剩余空间的长、宽、高相加，并计算其实际可利用空间的大小，循环遍历所有剩余箱子的体积大小与之比较，若剩余实际可利用空间大于某个箱子的体积，则将上下两层合为一层，放入对应的箱子，循环遍历直至无法放入（箱子可旋转）。

5）返回装箱结果，剩余货物个数及长宽高参数，剩余空间的最大剩余高度、最大剩余宽度、最大剩余长度。

流程图如图9所示。

3.1.3  函数的应用

1）在装载空间大于0，并且待装货物中有体积参数小于装载空间容积的箱子时，执行底层装载函数。

2）执行非底层装箱函数，在装载空间高度大于待装载箱子高度的情况下，循环执行非底层装载函数，（箱子可旋转）直至没有符合高度要求的箱子为止。

3）沿y轴增加，重复执行步骤1、步骤2，直至没有符合y轴剩余宽度的箱子为止。

流程图如10所示。

3.2  兼顾重心的调整优化策略

采用上述的算法已经可以得到初步的装填方式，但需要测试结果是否满足货物重心位置约束[6-7]。为了能让重心位置偏移量在可控的范围内，依据货物分层装填的特点，对各层物品进行同层旋转、上下层交换、同层水平移动等操作来实现重心位置的优化。

1）同层旋转。依据同一层“重”物在该层的几何中心为经验，进行旋转，来调整重心。

2）上下层交换。通过对相同的层之间进行交换，以将“重”物置于下层的经验来改变各层的位置来调整重心。

3）同层水平移动。考虑将同层的物品按“重”物居中的经验，通过水平移动层内物品来调整重心。

4  实例计算与结果分析

在JavaScript、Python的脚本语言和Django框架下基本完成了对该算法的检测并可对装填结果进行三维图像仿真展示[8-9]。为确认提出方案的可行性，采用算例数据进行试运行，7个算例的子算例有100个，箱子类型由少到多，异构性从弱到强，通过Python程序计算7组算例数据的体积利用率同时记录计算时间，算例结果见表1，仿真结果如图11所示。

由表1可以发现，随着箱子类型数量的增多，体积利用率呈现上升趋势，计算时间较短且不会随箱子类型的增多而延长计算时间。

5结论

随着智慧物流的不断发展，在运输过程中物体最密堆积空间利用率问题和重心偏移的物体越来越被重视，本文基于G2LA重心算法和同、异构货物二维、三维最密堆积算法提出了改进型兼顾重心问题的异构货物空间利用率最大化算法，初步解决了在空间利用率最大化的前提下运输过程中重心不稳的问题，对于智慧物流的发展具有重要意义。

参考文献：

[1] 景堃，周圣林，潘华.基于混合遗传算法的飞机转运集装箱布局优化设计[J].航空科学技术，2010（5）：36-38.

[2] 刘瑞瑞.基于遗传模拟退火算法的三维离线装箱优化问题研究[D].长春：吉林大学，2014.

[3] 张长勇，翟一鸣.基于改进遗传算法的航空集装箱装载问题研究[J].北京航空航天大学学报，2021，47（7）：1345-1352.

[4] 王岩，潘卫平，陈秋莲，等．单一尺寸长方体三维装箱问题的一种求解算法[J].包装工程，2015（11）：96-99.

[5] 薛莲.同一规格货物集装箱装载问题研究及其在物流行业的应用[D].天津：天津大学，2008.

[6] 张德富，彭煜，张丽丽．求解三维装箱问题的多层启发式搜索算法[J].计算机学报，2012，35（12）：2553-2561．

[7] 李伟，杨超宇，孟祥瑞.基于混合遗传算法的多品种货物装箱问题研究[J].包装与食品机械，2020，38（3）：51-56.

[8] FANSLAU T，BORTFELDT A． A tree search algorithm for solving the container loading problem[J]. Informs Journal on Computing，2010，22（2）：222-235．

[9] PARRE O F，ALVAREZ-VALDES Ｒ，OLIVEIRA J F，et al． Neighborhood structures for the container loading problem： a VNS implementation[J]． Journal of Heuristics，2010，16（1）：1-22．