基于LightGBM算法和出行链理论的电动汽车充电负荷多时间尺度预测模型
庞松岭 范凯迪 陈超 窦洁
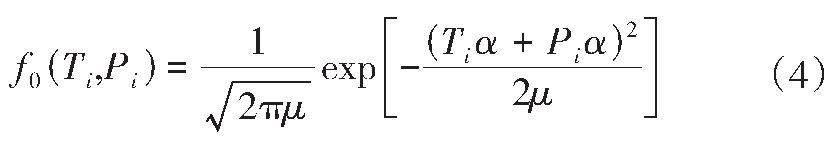
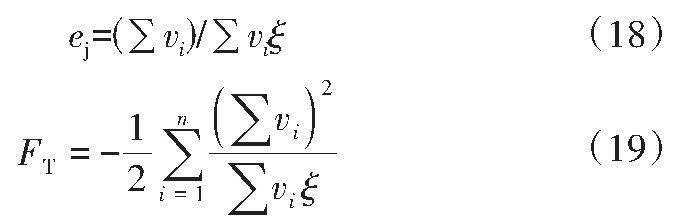
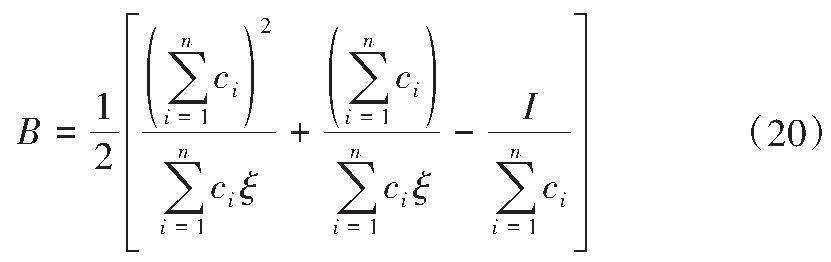
【摘要】为提高电动汽车充电负荷预测的准确性,设计了一种基于轻量级梯度提升机(LightGBM)算法和出行链理论的电动汽车充电负荷多时间尺度预测模型。利用出行链描述用户出行过程,采用蒙特卡洛法抽取时空数据,计算不同区域出行和停留时间的概率密度函数,采用牛顿法划分多时间尺度充电概率,明确驾驶时空分布与充电状况,并运用模糊数学定理与LightGBM分类充电负荷数据,构建了多季节多时段预测模型。采用LightGBM高效并行计算模式,明确充电负荷变化规律,实现了多时间尺度预测。试验结果表明:所建立的模型在不同季节和电动汽车数量条件下,预测误差低于100 kW,预测空报率低于3%,可准确展现充电负荷的变化规律。
主题词:轻量级梯度提升机 出行链理论 充电负荷 多时间尺度 预测模型
中图分类号:TM714 文献标志码:A DOI: 10.19620/j.cnki.1000-3703.20230993
A Multi Time Scale Prediction Model for Electric Vehicle Charging Load Based on LightGBM Algorithm and Travel Chain Theory
【Abstract】To improve the prediction accuracy of electric vehicle charging load, a multi time scale prediction model for electric vehicle charging load was designed based on the Lightweight Gradient Boosting Machine (LightGBM) algorithm and travel chain theory. The travel chain was used to describe the users travel process, Monte Carlo method was used to extract the spatiotemporal data, and the probability density functions of travel and stay time in different regions was calculated. Newton method was used to divide the probability of charging at multiple time scales, clarifying the spatiotemporal distribution of driving and charging conditions. Fuzzy mathematics theorem and LightGBM were applied to classify charging load data, and a multi season and multi time prediction model were constructed. The efficient parallel computing mode of LightGBM was applied which clarified the variation pattern of charging load, and multi time scale prediction was achieved. The experimental results show that the established model has a prediction error of less than 100 kW and a prediction false alarm rate of less than 3% under different seasons and the number of electric vehicles, and can accurately display the variation pattern of charging load.
Key words: Light Gradient Boosting Machine (LightGBM), Travel chain theory, Charging load, Multiple time scales, Prediction model
1 前言
电动汽车大规模充电带来的高用电量与强变化性使传统电网运行压力增大,电动汽车充电负荷预测有助于充电站规划科学的运营制度,对优化电网运行能力具有重要意义[1],是保证电网安全高效运行的关键。
吴丹等[2]基于XGBoost与轻量级梯度提升机(Light Gradient Boosting Machine,LightGBM)提出了电动汽车充电负荷预测模型,并采用岭回归(Ridge Regression,RR)算法进行求解,实现了负荷预测。张琳娟等[3]以出行起讫点(Origin-Destination,OD)时空分布矩阵为基础构建电动汽车负荷预测方法,基于蒙特卡洛方法建立电动汽车充电负荷预测模型,完成了负荷预测。张美霞等[4]建立了一种电动汽车出行时空转移模型,根据OD分析法模拟出行规律,凭借锂电池充放电试验信息确定不同温度对电池容量的影响,引入锚定效应分析用户心理与充电决策的关联关系,基于用户主观意愿构建了充电负荷预测模型。袁小溪等[5]对检测区域进行网格划分,以网格为空间预测单元,使用贝叶斯正则化反向传播(Back-Propagation,BP)神经网络法明确电动汽车充电负荷与各类影响因素的内在关联,实现充电需求预测。上述方法均未考虑充电负荷的时空变化特征,预测结果不够精准。
为了提高电动汽车充电负荷预测的准确性,本文采用出行链理论明确电动汽车用户出行时空规律,对每个特征量间的隐含关系进行近似线性关联分析,依据不同季节一天内多时段等多时间尺度,归一化计算车辆充电负荷多时间尺度指标,明确电动汽车的驾驶时空分布与充电状况,并基于改进的强回归树构建充电负荷多时间尺度预测模型,运用LightGBM算法高效率并行计算模式求解该模型,获得充电负荷多时间尺度预测结果,并通过试验验证所建立模型的有效性。
2 电动汽车充电负荷多时间尺度预测
2.1 出行链特征量近似线性关联分析
出行链表示用户在出行意愿支配下,从初始点出发,依照时间次序途经多个目标地点,最终抵达终点结束出行的过程。出行链特征量涵盖驾驶与停留2个部分。为完整定义用户出行流程,将出行链特征量分为时间特征量和空间特征量。
时间特征量能阐明电动汽车出行的时序改变状况,包含抵达、离开第i次出行目标地的时间Ti、TLi,离开第(i-1)次出行目的地开始第i次出行的时间TLi-1,第i次出行驾驶时间tgi、停留时间tsi。
空间特征量定义了电动汽车移动时的空间转移状况,包含初始出发地与终点的里程P0、第(i-1)次出行目的地里程(即第i次出行初始里程)Pi-1、第i次出行目的地里程Pi和出行的总里程p。
出行链每个特征量之间都具备耦合关系,时间链中,Ti与TLi可使用tgi、tsi获得:
Ti=TLi-1+tgi (1)
TLi=Ti+tsi (2)
同理,空间链中特征量的耦合关系为:
p=Pi+(P0-Pi-1) (3)
依照用户出行类别,将出行目标拟作回家、工作、购物、社交、其他事务5种类型[6-9]。将出行目的地划分为住宅区、工作区、商业区,且设定每个区域充电设备都能正常使用,出行链长度为3,即最多涵盖3个出行目标地。
为明确用户出行时空分布状况,以Pi、tgi、tsi的概率分布作为输入量,使用蒙特卡洛法随机抽取数据[10],产生不同的空间特征量。因当前电动汽车出行信息较少,将燃油车出行规律拟作电动汽车出行规律,经数据分析获得输入量概率分布结果。
假设用户出行时空基本符合正态分布[11],将其概率密度函数定义为:
式中:f0为用户第一次出行时段的概率密度函数;α为正态分布系数,此处为标准正态分布,因此取α=1;μ为密度分布系数,即概率密度函数的标准差。
概率密度函数的标准差σ为:
式中:f0(x)为概率密度函数,x为概率密度,[a,b]为函数定义域,τ为概率密度函数的均值。
概率密度函数的均值τ的计算公式为:
用户出行的行驶时间与行驶前、后的目标地类别相关,将其分成3个类别:从住宅区到非住宅区、从非住宅区到住宅区、从非住宅区到非住宅区[12-13]。假设3种行驶类型的时间均服从对数正态分布,将其概率密度函数定义为:
式中:μj为对数正态分布的均值,j=1,2,3分别表示从住宅区到非住宅区、从非住宅区到住宅区、从非住宅区到非住宅区。
电动汽车充电只能发生在抵达目标地后的停留过程中,因此每个目标区域的停留时间与充电模式的选择和充电时长直接相关[14-15]。将工作区停留时间的概率密度函数f(w)记作:
式中:tz为工作区的平均停留时间,w=(tsi-tz)/c为每个目标区域的停留时间,c为次数。
根据式(8)同理可得商业区与住宅区的停留时间概率密度。
不考虑交通堵塞,结合每个出行目标区域停留时间的概率密度,将时间链与空间链的特征量间进行耦合。整合不同时间尺度下的充电负荷数据与对应的地理位置信息,获取时间和空间上的充电负荷数据。从整合后的充电负荷数据中提取时间链和空间链的特征。运用统计和建模方法,研究不同时间尺度下的充电负荷对应的地理位置分布以及在不同地理位置上的充电负荷变化趋势等,进而获得电动汽车用户行驶里程:
Pi=f(w)vtgi (9)
式中:v为用户本次出行的平均车速。
通过近似线性关联分析出行链特征量,对时间链和空间链的特征量进行具体分析,获得电动汽车用户行驶里程,作为充电负荷多时间尺度预测的基础。
2.2 充电负荷多时间尺度预测模型构建
基于前文获得的行驶目的地概率密度和电动汽车用户行驶里程,从多时间尺度构建充电负荷预测模型。对历史充电负荷数据进行季节特征提取,通过季节分解法分析季节性变化的趋势和周期性。增加时间尺度的维度,以捕捉不同时间尺度上的季节变化。分析后发现,季节变化中气温是负荷的主要影响因素[16],因此在构建模型前,需进行负荷数据和气温数据的归一化处理。将不同季节(季节时间尺度)一天之内多时段(小时尺度)的负荷数据归一化到[0,1]范围,使用最大-最小归一化方法,将负荷数据映射到指定范围内,以便统一比较和分析不同季节、不同时段的负荷数据。采用量化因子归一化处理方式量化处理负荷数据的时间尺度指标。考虑气温对负荷的影响,因不同季节一天之内气温会发生变化,过冷或过热均需要启动空调,负荷将发生变化,因此将气温作为负荷数据归一化指标,将气温的归一化形式记作:
Yt=(ut-umin)(ut-umax) (10)
式中:Yt为t时段归一化后的温度,ut为t时段实时气温,umin、umax分别为最低、最高气温。
现阶段,电动汽车多为每天充电一次或设置固定的充电模式,但用户驾驶至某目的地时是否选择充电与剩余电量有很大关系,一般剩余电量在40%以上才能保证电动汽车正常运行[17]。基于前文的电动汽车用户行驶里程,计算第i次出行结束时的电池荷电状态Ri:
[RiG=Ri-1G-ziP] (11)
式中:G为电池容量,zi为第i次出行的每公里耗电量。
由此获得约束电动汽车行驶至目的地时的充电条件为:
[RiG-zi+1Pi+1<0.4G] (12)
电动汽车充电时间由电池容量、起始荷电状态与充电功率等因素决定[18-20]。如果在目的地充电,则充电时间为:
Tc=[(1-Ri-1)G+zip]/kQ (13)
式中:k为充电效率,Q为充电功率水平。
牛顿法利用函数的一阶和二阶导数信息逐步逼近函数的根。在划分充电概率的问题中,牛顿法可以将充电概率视为一个函数,通过迭代近似求解该函数的根,优化了充电概率的计算过程,辅助提高了充电概率计算的收敛性和稳定性。因此,在上述各项指标基础上,采用牛顿法划分多时间尺度的充电概率[21-22],即可明确电动汽车的驾驶时空分布与充电状况,获得其在各目的地的充电负荷。若汽车到达目的地后,通过充电概率可以推算当前剩余电量,并评估能否满足下个行程的驾驶需求,基于牛顿法将电动汽车处于t时段的充电概率Jt表示为:
式中:Ty为驾驶到目的地的行程终止时间段。
同时,运用加法模式训练,得到预测改进回归树模型Bt,记作:
式中:ci、di分别为损失函数一阶与二阶梯度统计结果,Di为叶子样本数据集,β为惩罚系数,n为数据量,ai为分类系数,fi为负荷数据的第i棵分类决策树(即第i次出行)。
改进回归树模型的训练流程为:
a. 选择特征。从所有特征中选取一个最优的特征作为当前节点的分裂特征。
b. 划分数据。根据选定的分裂特征将数据集划分成2个子集,每个子集包含具有相同特征值的样本。
c. 计算误差。使用某个指标(例如均方误差)计算每个子集中实际值与预测值间的误差。
d. 如果满足迭代次数最大条件,则将当前节点标记为叶节点,并结束流程,否则转到步骤e。
e. 递归划分数据。对于每个子集,重复步骤a~步骤d,直到满足停止条件。
为探寻最能反映因变量本质的自变量特征,完成多时间尺度充电负荷数据分类工作,将i棵弱回归树线性融合成强回归树,强回归树可降低数据内存占用量,确保在不降低计算速率的基础上训练更多数据,提高运算准确率。由此完成改进回归树模型的训练,作为预测的基础数学模型。
充分考虑前文获得的汽车停留充电的时空概率密度,累加每个时间尺度的电动汽车充电负荷,基于训练后的改进回归树模型构建充电负荷多时间尺度预测模型为:
式中:Jc为充电功率水平,Nh为充电车辆总数,Ji,t为第i次出行目的地t时段的充电功率。
了解电动汽车出行规律后可知,车辆充电负荷预测存在多种随机元素,上述基于改进回归树模型的充电负荷多时间尺度预测模型获得的预测结果在随机元素干扰下难以获得最优解,因此需要选择合适的算法求解模型的最优值。
2.3 充电负荷多时间尺度预测求解
模糊数学原理普遍用于处理不确定性和模糊性的问题。LightGBM通过多个基学习器的集成,可以有效减少复杂问题求解过拟合的风险,能够处理离散型和混合型数据。因此,运用模糊数学定理与LightGBM可以完成随机元素推导,适用于求解前文构建的充电负荷多时间尺度预测模型这种复杂的数据模型。
利用LightGBM算法训练前文的改进回归树模型,获得多时间尺度负荷预测的分类求解结果。将LightGBM算法下的回归树模型表示为:
式中:T为全部树总棵数,A为叶子数量。
训练过程为:
a. 初始化。将训练集中的所有样本视为一个叶节点,并计算它们的均值作为初始预测值。
b. 迭代训练。在每次迭代中,首先计算当前模型的残差(即实际值与当前预测值的差),然后训练一个新的回归树模型来拟合残差。
c. 叶节点分裂。对于每个叶节点,根据某个指标(例如最小化方差或最小化绝对误差)选择最优的分裂特征和分裂点,将该叶节点分裂成2个子节点。
d. 剪枝。使用正则化方法(例如最小化叶节点数或最小化复杂度)对生成的树进行剪枝,以避免过拟合。
e. 更新预测值。对于每个叶节点,用该节点的均值作为该节点上所有样本的预测值。
f. 循环迭代。重复步骤b~步骤e,直到达到预定的迭代次数或满足其他停止条件。
在已知树结构的情况下,设置各叶子节点vi内的最佳叶子质量分数ej与全部树集合的极值FT,计算公式分别为:
式中:ξ为节点权值。
对式(17)引入模糊数学原理中的拆分计算,基于LightGBM算法的充电负荷预测多时间尺度分类求解结果为:
式中:B为充电负荷结果数据量,I为样本集样本数量总和。
电动汽车充电负荷多时间尺度预测方法流程如图1所示。
3 试验验证与结果分析
3.1 试验准备
依照相关电力标准,设定居住地与公共场所的充电功率水平分别为3.5 kW、20.3 kW。电动汽车数量参照某市2022年6月汽车保有量520.3×104 辆的0.1%取整为5 200辆。利用MATLAB平台完成验证分析,以出行链夏、冬季为不同检验场景。
区域内建设的充电站每天需完成3辆以上汽车的充电服务,汽车充电等待时间不超过30 min。该区域内最多可布署11个充电站,且不少于5个,区域内电动车抵达目标地充电站的行驶距离小于1 km。充电站的分布概率密度为0.5,电动汽车在各充电站充电的分布概率密度为0.42,停留时间概率分布密度为0.42。
电动汽车参数如表1所示。
电动汽车恒充电功率水平为4.0 kW,采取每天充电一次的模式,部分历史数据如表2所示,作为后续数据分析的依据。
对电动汽车充电负荷数据进行清洗补缺,以提升预测精度。
编写试验算法伪代码如下:
# 输入:清洗和补缺后的充电负荷数据
# 输出:充电负荷多时间尺度预测结果
# 使用模糊数学原理和LightGBM算法实现充电负荷多时间尺度预测模型
# 训练LightGBM模型
model = train_lightgbm_model(data) # data为清洗和补缺后的充电负荷数据
# 使用训练好的模型进行预测
predictions = model.predict(test_data) # test_data为测试数据
# 返回预测结果
return predictions
# 执行试验
result = run_experiment()
# 输出试验结果
print(result)
3.2 试验结果分析
3.2.1 出行链时间尺度特征量关联分析
使用所提出的模型预测夏季和冬季伴随电动汽车数量的改变,充电负荷的变化情况,结果如图2所示。
由图2可知,不同电动汽车数量充电负荷对初始负荷存在影响,继而影响负荷预测结果,因此以电动汽车数量作为变量,能够测试本文预测结果与理想值的差距。
3.2.2 充电负荷多时间尺度预测效果
将不同电动汽车数量和不同时间尺度作为变量因素,本文将不同季节、一天内不同时间作为多时间尺度测试本文模型的预测效果,季节时间尺度下充电负荷预测效果如图3所示。
从图3中可以看出,所提出模型得到的不同电动汽车数量条件下充电负荷趋势的峰谷差与理想值基本一致,误差低于100 kW,证明模型在不同季节及电动汽车数量条件下仍能够有效预测。这是因为本文采用牛顿法明确了充电负荷变化规律,不受时间尺度变化影响。
3.2.3 充电负荷多时间尺度预测求解精度测试
为进一步验证方法的预测精度,将XGBoost[2]与LightGBM预测法、OD时空分布矩阵预测法[3]、动态能耗法[4]、网格划分法[5]作为对照组与本文提出的方法共同进行试验对比。从电动汽车充电负荷历史数据中随机抽取一天的数据作为样本,在该样本中,电动汽车数量仍为5 200辆,恒充电功率水平为4.0 kW,并采取每天充电一次的模式。分别采用5种方法进行日均充电负荷预测,结果如图4所示。
从图4中可以看出,因本文提出的方法全面考虑了充电场所区域的多样性,计算得到的负荷曲线更加精准,与其他方法相比更具计算优势。
使用空报率指标检验5种方法的负荷预测性能,空报率表示错误预测结果在全部预测结果中的占比,占比越小,证明预测能力越优秀。设定共进行800次试验,取每100次试验的空报率均值进行对比,结果如图5所示。
由图5可知,本文提出的方法的空报率始终低于3%,显著小于其他方法,在实际应用中更能展现出不同时间尺度下电动汽车充电负荷变化规律,预测性能更好。这是因为本文构建的预测模型融合考虑了不同季节时间尺度下温度对负荷的影响的变化、不同时段负荷变化,获得了较高的负荷预测精度。
4 结束语
提升电动汽车充电负荷预测准确性,对确保电网的安全运行尤为关键,本文提出一种基于LightGBM算法和出行链理论的电动汽车充电负荷多时间尺度预测模型。试验结果表明,该模型在不同季节和电动汽车数量条件下,预测误差和预测空报率均较低,能准确预测充电负荷变化。
本文方法在现阶段得到了较好的预测结果,但电动汽车充电负荷预测过程细节还有待优化,具体体现在:
a. 充电负荷数据的优化采集与分类。充电行为具有一定的规律性,往往存在明显的周期性变化,且不同车型、不同充电设备、不同充电策略等均对充电负荷产生影响。因此,负荷数据采集难度较大。
b. 需进一步考虑跨时段充电负荷预测的研究。这需要结合日历信息和行驶轨迹等数据,提高对充电行为的建模和分析能力。
参 考 文 献
[1] 刘志强, 张谦, 朱熠, 等. 计及车-路-站-网融合的电动汽车充电负荷时空分布预测[J]. 电力系统自动化, 2022, 46(12): 36-45.
LIU Z Q, ZHANG Q, ZHU Y, et al. Spatial-Temporal Distribution Prediction of Charging Loads for Electric Vehicles Considering Vehicle-Road-Station-Grid Integration[J]. Automation of Electric Power Systems, 2022, 46(12): 36-45.
[2] 吴丹, 雷珽, 李芝娟, 等. 基于XGBoost与LightGBM集成的电动汽车充电负荷预测模型[J]. 电子技术应用, 2022, 48(9): 44-49.
WU D, LEI T, LI Z J, et al. Electric Vehicle Charging Load Forecasting Based on XGBoost and LightGBM Integration Model[J]. Application of Electronic Technique, 2022, 48(9): 44-49.
[3] 张琳娟, 许长清, 王利利, 等. 基于OD矩阵的电动汽车充电负荷时空分布预测[J]. 电力系统保护与控制, 2021, 49(20): 82-91.
ZHANG L J, XU C Q, WANG L L, et al. OD Matrix Based Spatiotemporal Distribution of EV Charging Load Prediction[J]. Power System Protection and Control, 2021, 49(20): 82-91.
[4] 张美霞, 吴子敬, 杨秀. 基于动态能耗模型与用户心理的电动汽车充电负荷预测[J]. 现代电力, 2022, 39(6): 710-719.
ZHANG M X, WU Z J, YANG X. Electric Vehicle Charging Load Prediction Based on Dynamic Energy Consumption Model and User Psychology[J]. Modern Electric Power, 2022, 39(6): 710-719.
[5] 袁小溪, 潘鸣宇, 段大鹏, 等. 基于网格划分的电动汽车充电负荷预测方法[J]. 电力科学与技术学报, 2021, 36(3): 19-26.
YUAN X X, PAN M Y, DUAN D P, et al. Prediction Method of Electric Vehicle Charging Load Based on Grid Division[J]. Journal of Electric Power Science and Technology, 2021, 36(3): 19-26.
[6] 杨梅, 李忠, 吴昊, 等. 基于多尺度时间特征LSTM的短期负荷预测[J]. 控制工程, 2022, 29(9): 1722-1728.
YANG M, LI Z, WU H, et al. Short-Term Load Prediction of LSTM Based on Multi-Scale Time Characteristics[J]. Control Engineering of China, 2022, 29(9): 1722-1728.
[7] 李香龙, 马龙飞, 赵向阳, 等. 基于LSTM网络的时间多尺度电采暖负荷预测[J]. 电力系统及其自动化学报, 2021, 33(4): 71-75.
LI X L, MA L F, ZHAO X Y, et al. Multi-Time Scale Electric Heating Load Forecasting Based on Long Short-term Memory Network[J]. Proceedings of the CSU-EPSA, 2021, 33(4): 71-75.
[8] 张雅雯, 王志海, 刘海洋, 等. 基于多尺度残差FCN的时间序列分类算法[J]. 软件学报, 2022, 33(2): 555-570.
ZHANG Y W, WANG Z H, LIU H Y, et al. Time Series Classification Algorithm Based on Multiscale Residual Full Convolutional Neural Network[J]. Journal of Software, 2022, 33(2): 555-570.
[9] 刘杰, 金勇杰, 田明. 基于VMD和TCN的多尺度短期电力负荷预测[J]. 电子科技大学学报, 2022, 51(4): 550-557.
LIU J, JIN Y J, TIAN M. Multi-Scale Short-Term Load Forecasting Based on VMD and TCN[J]. Journal of University of Electronic Science and Technology of China, 2022, 51(4): 550-557.
[10] 李恒杰, 朱江皓, 傅晓飞, 等. 基于集成学习的电动汽车充电站超短期负荷预测[J]. 上海交通大学学报, 2022, 56(8): 1004-1013.
LI H J, ZHU J H, FU X F, et al. Ultra-Short-Term Load Forecasting of Electric Vehicle Charging Stations Based on Ensemble Learning[J]. Journal of Shanghai Jiaotong University, 2022, 56(8): 1004-1013.
[11] 刘晓天, 傅军, 赵思翔, 等. 基于二层规划并计及负荷预测的电动汽车充电桩选址定容方法[J]. 电测与仪表, 2021, 58(5): 144-150.
LIU X T, FU J, ZHAO S X, et al. Location and Capacity Determination Method of Electric Vehicle Charging Pile Based on Bi-Level Programming and Considering Load Forecasting[J]. Electrical Measurement & Instrumentation, 2021, 58(5): 144-150.
[12] 秦建华, 李娜, 金泰, 等. 基于Vosviewer与Citespace对电动汽车充电负荷领域的计量分析[J]. 科学技术与工程, 2022, 22(10): 4196-4205.
QIN J H, LI N, JIN T, et al. Metrological Analysis of Electric Vehicle Charging Load Based on Vosviewer and Citespace[J]. Science Technology and Engineering, 2022, 22(10): 4196-4205.
[13] 李楠, 马宏忠. 基于综合预测模型和蒙特卡洛的电动汽车保有量及负荷预测方法研究[J]. 电机与控制应用, 2022, 49(12): 74-80.
LI N, MA H Z. Research on Electric Vehicle Ownership and Load Prediction Method Based on Comprehensive Prediction Model and Monte Carlo[J]. Electric Machines & Control Application, 2022, 49(12): 74-80.
[14] 林铭蓉, 胡志坚, 高明鑫, 等. 基于时空规律的电动汽车负荷建模及其自动需求响应[J]. 南方电网技术, 2022, 16(1): 99-107.
LIN M R, HU Z J, GAO M X, et al. Electric Vehicle Load Modeling and Automatic Demand Response Based on Space-Time Law[J]. Southern Power System Technology, 2022, 16(1): 99-107.
[15] 姚志力, 江斌开, 龚春阳, 等. 计及电动汽车充电负荷特性的区域多能源站规划设计[J]. 电网技术, 2022, 46(9): 3304-3318.
YAO Z L, JIANG B K, GONG C Y, et al. Planning and Design of Regional Multi-Energy Stations Considering Electric Vehicle Charging Load Characteristics[J]. Power System Technology, 2022, 46(9): 3304-3318.
[16] 罗浩成, 胡泽春, 张洪财. 环境温度对电动汽车充电负荷的影响分析[J]. 电力建设, 2015, 36(7): 69-74.
LUO H C, HU Z C, ZHANG H C. Effect Analysis of Ambient Temperature on Electric Vehicle Charging Load[J]. Electric Power Construction, 2015, 36(7): 69-74.
[17] 蔡海青, 代伟, 赵静怡, 等. 基于多参数规划的电动汽车充电站有效容量评估方法[J]. 中国电力, 2022, 55(11): 175-183.
CAI H Q, DAI W, ZHAO J Y, et al. Available Capacity Evaluation Method of Electric Vehicle Charging Stations Based on Multi-Parametric Programming[J]. Electric Power, 2022, 55(11): 175-183.
[18] 朱磊, 黄河, 高松, 等. 计及风电消纳的电动汽车负荷优化配置研究[J]. 中国电机工程学报, 2021, 41(增刊1): 194-203.
ZHU L, HUANG H, GAO S, et al. Research on Optimal Load Allocation of Electric Vehicle Considering Wind Power Consumption[J]. Proceedings of the CSEE, 2021, 41(S1): 194-203.
[19] 方娜, 李俊晓, 陈浩, 等. 基于CNN-GRU-MLR的多频组合短期电力负荷预测[J]. 计算机仿真, 2023, 40(1): 118-124.
FANG N, LI J X, CHEN H, et al. Multi-Frequency Combination Short-Term Power Load Forecasting Based on CNN-GRU-MLR[J]. Computer Simulation, 2023, 40(1): 118-124.
[20] 史亮, 葛晓琳, 顾闻, 等. 考虑需求响应的电动汽车充电负荷研究[J]. 电测与仪表, 2022, 59(7): 42-47.
SHI L, GE X L, GU W, et al. Research on Charging Loads of Electric Vehicles Considering Demand Response[J]. Electrical Measurement & Instrumentation, 2022, 59(7): 42-47.
[21] 江友华, 屈靖洁, 曹以龙, 等. 考虑风电-负荷及综合需求响应不确定性的能量枢纽双层优化运行及配置方法[J]. 电测与仪表, 2022, 59(3): 117-124.
JIANG Y H, QU J J, CAO Y L, et al. Double-Layer Optimal Operation and Configuration Method for Energy Hub Considering Uncertainty of Wind Power-Load and Integrated Demand Response[J]. Electrical Measurement & Instrumentation, 2022, 59(3): 117-124.
[22] 徐蕙, 陈平, 李海涛, 等. MPSR-MKSVM电力负荷预测综合优化策略[J]. 电测与仪表, 2022, 59(1): 77-83.
XU H, CHEN P, LI H T, et al. Comprehensive Optimization Strategy of Power Load Forecasting Based on MPSR-MKSVM[J]. Electrical Measurement & Instrumentation, 2022, 59(1): 77-83.

