双态噪声驱动的分数阶星型耦合网络的随机共振

钟苏川 高仕龙 史思红 张路

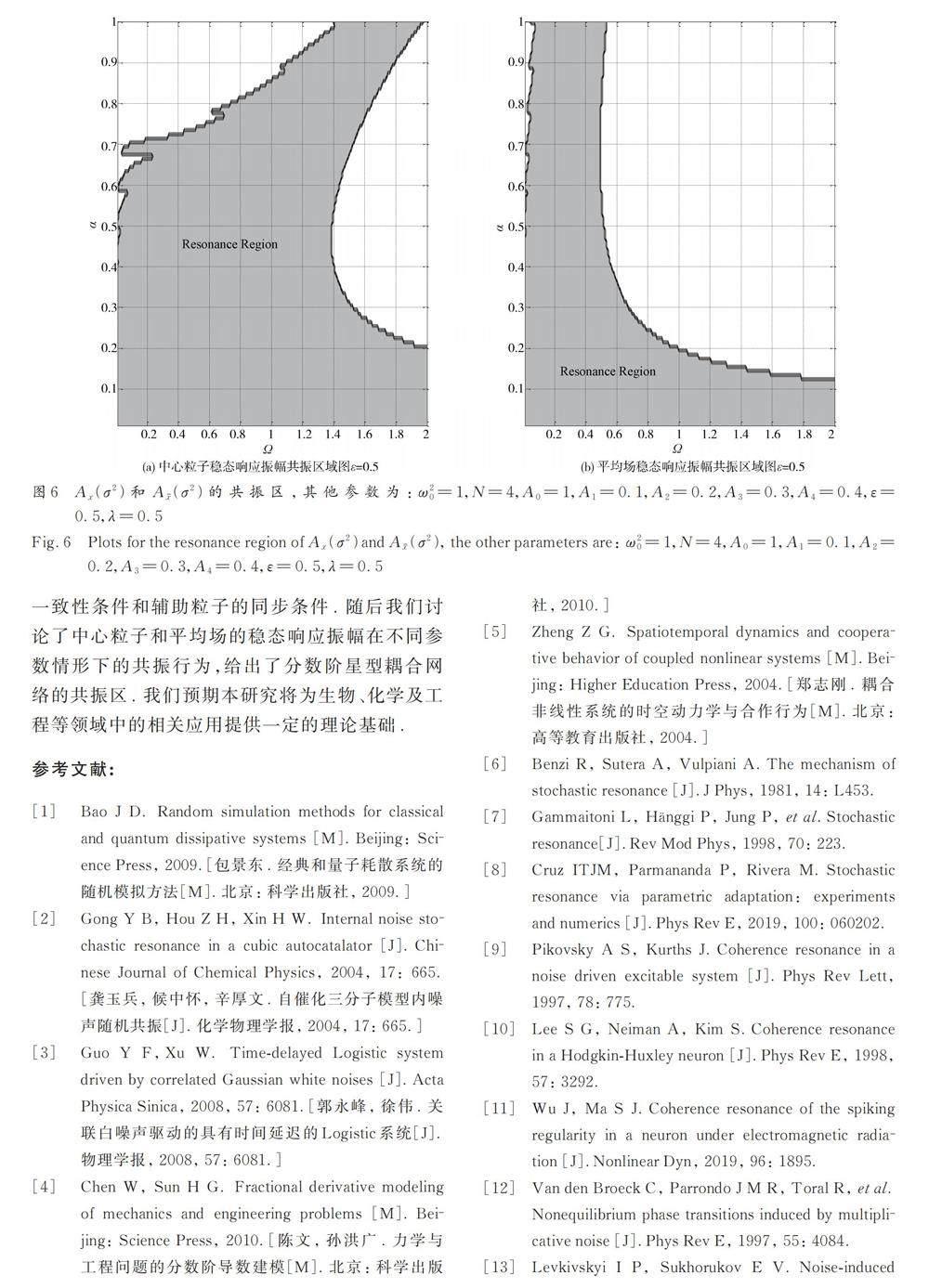
摘 要： 本文研究了一类分数阶星型耦合网络模型的随机共振行为，该网络由一个中心粒子和多个耦合粒子组成，其中粒子的耦合强度受到双态噪声的扰动. 本文将耦合粒子运动轨迹的算术平均值定义为系统的平均场，然后分别讨论了中心粒子和平均场的统计特征和共振行为. 利用随机平均法及变换技巧，本文首先推导了中心粒子和平均场的一阶稳态矩和稳态响应振幅的表达式，然后分析了中心粒子和平均场的运动轨迹的一致性条件以及耦合粒子的同步条件，最后数值研究了中心粒子和平均场的共振行为. 仿真结果显示，网络存在丰富的共振行为：中心粒子和平均场的稳态响应均可能出现“单峰共振”“单峰-单谷共振”“单谷-单峰共振”及“逆共振”等共振行为，说明中心粒子和平均场的稳态响应对参数的依赖性很高. 此外，本文还基于中心粒子和平均场的稳态响应振幅给出了模型的共振区. 本研究可望为分数阶星型网络共振行为的控制提供理论基础.

关键词： 星型耦合网络； 随机共振； 双态噪声； 分数阶Langevin 系统

中图分类号： O29 文献标志码： A DOI： 10. 19907/j. 0490-6756. 2024. 031001

1 引言

在许多应用系统（ 如物理系统、生化系统）中，随机涨落现象普遍存在. 对于小尺度反应系统而言，随机涨落起着关键作用. 引起涨落的主要原因是系统本身的运动产生的内噪声及外部环境波动产生的外噪声［1-4］. 外噪声即通常所说的随机力，一般被视为消极性干扰. 然而，近年来非线性科学和统计物理学的研究揭示，无规则的随机力并不总是对宏观秩序起消极破坏作用，在一定条件下它在产生相干运动和建立“序”上起十分积极的创造性作用［5］. 因此，揭示非线性条件下随机力产生的各种效应，如随机共振（Stochastic Resonance，SR）［6-8］、相干共振（Coherent Resonance，CR）［9-11］、噪声诱导相变（Noise Induced Phase Transition）［12-13］和布朗马达（Brownian Motor）［14-16］等，成为非线性科学和统计物理研究中的一个热点.

近年来，分数阶微积分理论受到极大关注. 在黏弹性材料、色噪声、混沌、反常扩散等现象的研究中，分数阶微积分理论有广泛的应用. 分数阶微积分可以描述具有时间记忆性和长程空间相关性的演化过程，比整数阶微积分更适合于描述有记忆和遗传、路径依赖性质的物理过程和生化反应过程. 特别地，对随机力作用下的分数阶朗之万方程或广义朗之万方程的共振行为的研究已有不少. 其中，Mankin 等［17-19］对双态和三态噪声驱动的分数阶线性朗之万方程进行了研究，分析了乘性噪声驱动的线性分数阶线性朗之万方程的各种广义随机共振现象及机理. Zhong 等［20-22］研究了单个分数阶随机动力系统在不同参数涨落、时延影响下的共振行为. 这些研究为分数阶动力系统的随机共振成为一个新研究方向提供了可能.

然而，仅对单个随机动力系统的共振行为展开研究还不够充分. 事实上，复杂系统的涌现行为意味着我们业需要研究具有相互作用的大量个体所组成的复杂、耦合系统. 在复杂网络系统中，个体之间的合作行为有多种多样的表现形式. 从个体耦合形式来看，耦合系统可以分为线性耦合和非线性耦合、最近邻耦合、全局耦合和星型耦合网络，等［23］. 此外，由于环境波动和系统内部涨落的普遍存在，随机力广泛存在于各网络中. 因此，研究受随机力影响的网络系统的随机动力学行为具有现实意义.

同步和共振作为典型的集群动力学行为，是随机动力学和网络科学研究领域的一个新前沿和交叉点［24］. 在这方面，Lin 等［25， 26］研究了随机耦合粒子在复杂环境中的集体输运行为，揭示了输运速度所具有的随机共振和相干共振等行为对系统参数和环境的依赖性. Gao 等［27］研究了耦合系数的幂律异质性对一类双稳中心耦合系统集体行为的影响，观测到共振、非共振、亚共振和超共振等现象. Xia 等［28］从理论和数值仿真的角度研究了具有质量涨落的双分数阶耦合谐振子系统的多种随机共振行为及其产生机理. Ni 等［29］研究了随机中心耦合布朗马达的定向输运与随机共振现象，分析了耦合系统结构参数和噪声对粒子输运及共振的影响. Lin 等［30］研究了具有截断Mittag-Leffler 噪声的质量涨落耦合振子的集体共振行为及其对模型参数的非单调依赖性.

就我们所知，目前对分数阶星型耦合网络的随机共振行为及噪声作用机理的研究还很少见，本文正是这方面研究的一个尝试. 我们的分数阶星型耦合网络模型由一个中心粒子和N 个完全相同的辅助粒子构成. 为研究方便，我们将环境的扰动作用于耦合强度上的随机力建模为双态噪声.通过将N 个辅助粒子的运动轨迹的算术平均定义为模型的平均场，我们将中心粒子和平均场作为主要研究对象. 我们以随机平均和变换法求解为研究手段，推导获得了中心粒子和平均场响应的一阶稳态矩和稳态响应振幅的解析表达式，分析了中心粒子和平均场的运动轨迹的一致性条件及耦合粒子的同步条件. 最后，基于网络中心粒子和平均场的稳态响应振幅的解析表达式，我们研究了在不同参数组合情况下中心粒子和平均场稳态响应振幅的共振行为. 仿真结果表明，中心粒子和平均场都可以产生“单峰共振”、“单峰-单谷共振”、“单谷-单峰共振”和“逆共振”等多种共振行为，表明网络的稳态响应振幅对参数的强依赖性.