基于深度学习的“函数的单调性”概念教学
左婷

课题信息:江苏省教育科学“十四五”规划2022年度课题“指向深度学习的高中数学单元教学策略研究”,立项编号为C/2022/02/05.
1 深度学习的基本思维
1.1 概念内涵的深层理解
基于数学概念课堂的教学实践与深度学习,从概念层面挖掘,剖析概念的内涵与实质,以及相关概念的来龙去脉与关联,从而联系相关概念的外延与应用,全面构建数学知识体系,形成不同概念之间的节点与联系,促进不同数学知识之间的转化与应用.
1.2 数学思维的深层应用
基于数学概念课堂的教学实践与深度学习,由知识到思维逐步深入,借助构造、类比、联系、创新等思维方式,展示知识所对应的思维,加深对知识的理解与掌握,从思维层面形成数学习惯,构建更加良好的思维品质与核心素养.
1.3 创新应用的深层拓展
基于深度学习,有效构建数学知识、数学思想、数学经验等方面之间的融合,形成更加完善与系统的知识网络体系与架构,对于数学应用与创新应用等都有较好的提升与拓展作用.
2 深度学习的教学过程
2.1 导学聚焦
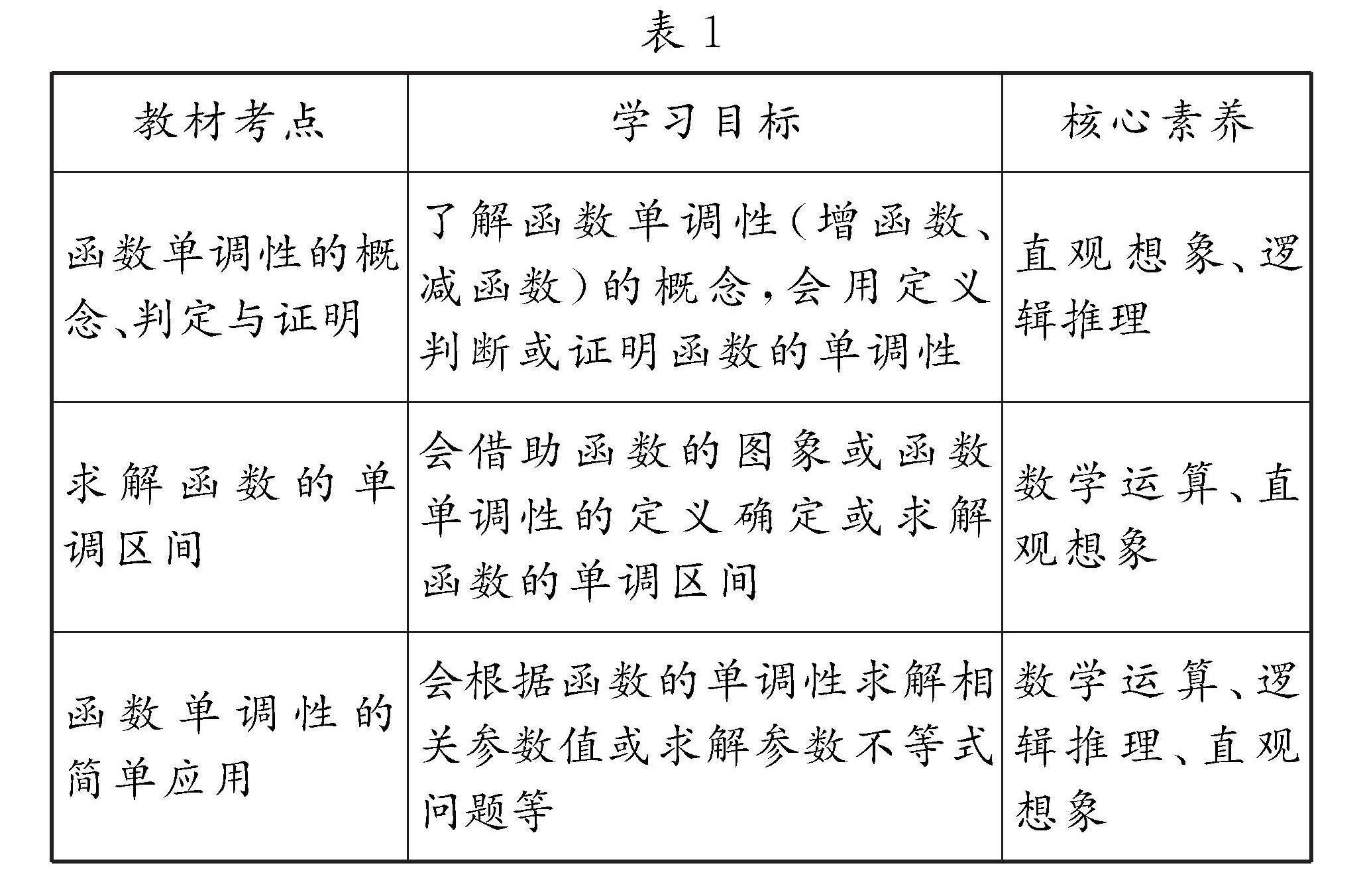
基于深度学习的“函数的单调性”概念教学的导学聚焦如表1.
表1
教材考点
学习目标
核心素养
函数单调性的概念、判定与证明
了解函数单调性(增函数、减函数)的概念,会用定义判断或证明函数的单调性
直观想象、逻辑推理
求解函数的单调区间
会借助函数的图象或函数单调性的定义确定或求解函数的单调区间
数学运算、直观想象
函数单调性的简单应用
会根据函数的单调性求解相关参数值或求解参数不等式问题等
数学运算、逻辑推理、直观想象
2.2 问题导学
预习教材(人教A版数学必修第一册)第三章第二节“函数的基本性质”,对应教材的位置是第76~79页,并思考下列相关问题:
(1)如何定义单调递增与单调递减?增函数、减函数的概念又是怎样的?
(2)函数的单调性与函数图象变化规律有何关系?函数的单调性和其对应的单调区间有何关系?
2.3 情境引入
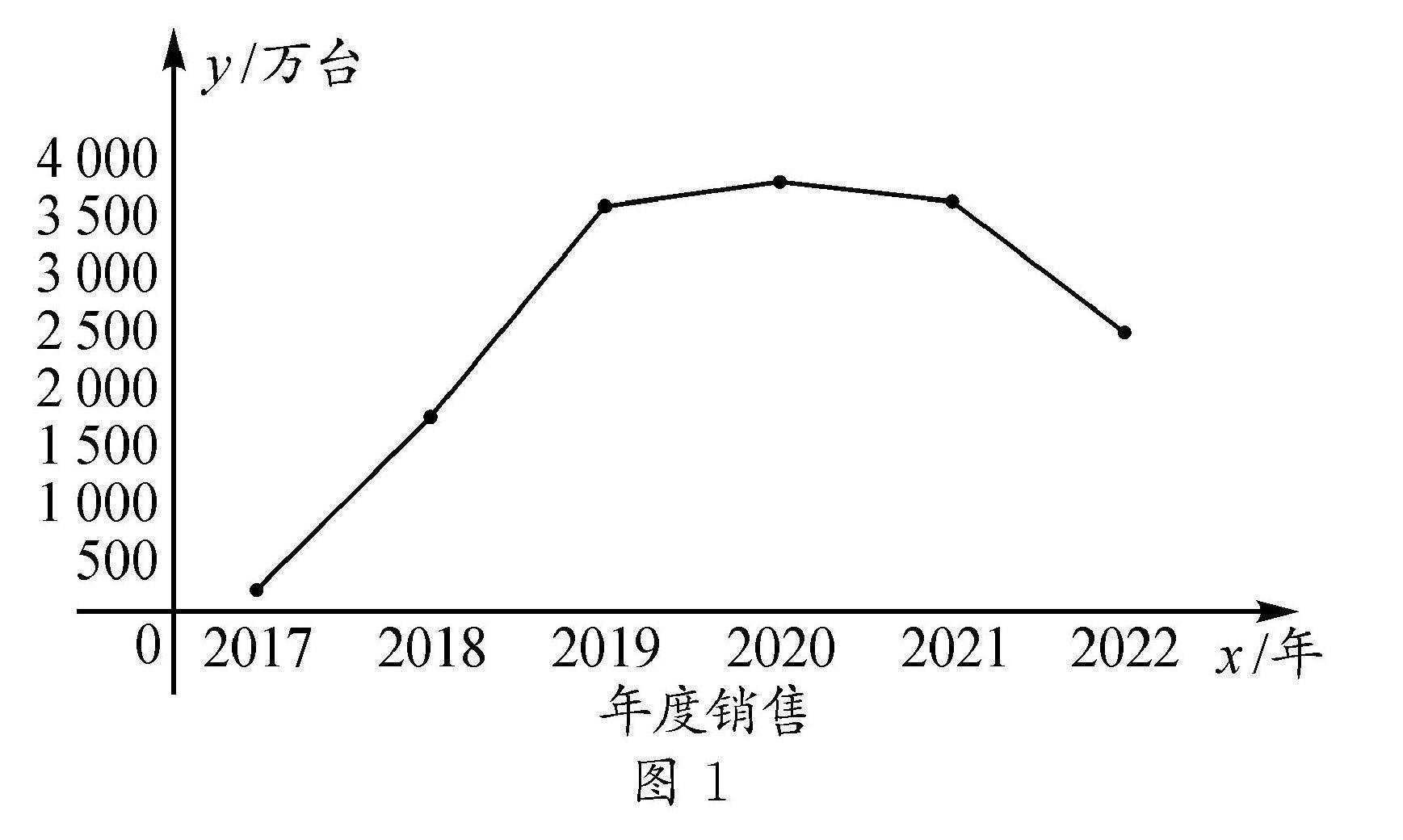
材料1:目前,国内市场销量前三的智能音响分别是:第三名,天猫精灵(浙江);第二名,小爱同学(北京);第一名,小度(北京).图1是2017—2022年中国智能音响市场销售量变化图.
问题1 (1)上述情境中变量分别是什么,哪一个变量随着另一个变量的变化而变化?
(2)从左到右,图象的变化规律是什么?
材料2:二十四节气,是中华民族悠久历史文化的重要组成部分.我们的祖先通过它能直观地了解一年中季节气候的变化规律,它在安排和指导农业生产中,发挥了重大作用.图2是某地一年的气温变化图.
问题2 气温随着时间的改变如何变化,图象的变化规律是什么?
2.4 新知探究
(1)增函数、减函数的概念
一般地,设函数f(x)的定义域为I,区间DI:
①如果x1,x2∈D,当x1<x2时,都有f(x1)<f(x2),那么就称函数f(x)在区间D上单调递增(如图3).
②如果x1,x2∈D,当x1<x2时,都有f(x1)>f(x2),那么就称函数f(x)在区间D上单调递减(如图4).
特别地,
当函数f(x)在它的定义域上单调递增(减)时,我们就称它是增(减)函数.
【微思考1】①在函数单调性的定义中,能否去掉“任意”?
(提示:不能.不能用特殊代替一般)
②x1,x2∈D,若(x2-x1)[f(x2)-f(x1)]>0,则y=f(x)在某个区间D上单调递增吗?若(x2-x1)[f(x2)-f(x1)]<0,则y=f(x)在某个区间D上单调递减吗?简要说明原因.
(提示:是.若(x2-x1)[f(x2)-f(x1)]>0则x2-x1与f(x2)-f(x1)同号,即x2>x1时,f(x2)>f(x1),所以f(x)在D上单调递增;
同理(x2-x1)[f(x2)-f(x1)]<0时,f(x)在D上单调递减.)
③x1,x2∈D,若f(x2)-f(x1)x2-x1>0,则y=f(x)在区间D上单调递增吗?若f(x2)-f(x1)x2-x1<0,则y=f(x)在区间D上单调递减并简要说明原因.(
提示:是.若f(x2)-f(x1)x2-x1>0,则x2-x1与f(x2)-f(x1)同号,即x2>x1时,f(x2)>f(x1),所以f(x)在D上单调递增;
同理f(x2)-f(x1)x2-x1<0时,f(x)在D上单调递减.)
(2)函数的单调性与单调区间
如果函数y=f(x)在区间D上单调递增或单调递减,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间.
【微思考2】区间D一定是对应函数的定义域吗?(
提示:不一定,可能是定义域的一个子区间,单调性是局部概念,不是整体概念.)
2.5 新知应用
(1)函数单调性的判定与证明
例1 根据定义,研究函数f(x)=axx—1(a≠0)在x∈(-1,1)上的单调性.(a>0时,单调递减;a<0时,单调递增.)
点评:利用函数的单调性的定义判断和证明函数单调性的基本步骤如图5所示.
这里要注意:作差变形是判断和证明函数单调性的关键所在,且变形的结果多为几个因式乘积的形式.
(2)函数单调区间的确定与求解
例2 画出函数y=|-x2+2x+3|的图象,并指出函数的单调区间.(增区间为[-1,1],[3,+∞);减区间为(-∞,-1],(1,3).)
点评:确定与求解函数的单调区间的两种常见方法如图6所示.
3 深度学习的教学启示
基于数学概念课堂的教学实践与深度学习,立足数学基础知识,特别是数学概念与性质所对应的内涵,从而从概念或性质等视角切入,进行多视角的深度学习,对于基础性的把握更加到位.
借助深度学习,将相应的数学概念进行“串点成线、织网铺面”,构建一个完善的数学知识体系,从而有效夯实学生的“四基”,培养学生的“四能”,强化创新意识与创新应用,培育理性思维,促进学生高阶思维、核心素养的发展.

