改进蚁群算法在农村垃圾治理问题中的应用

李婷

李 婷. 改进蚁群算法在农村垃圾治理问题中的应用［J］. 湖北农业科学，2024，63（3）：255-259．

摘要：为了减少农村垃圾治理的运输费用，通过引入节约因子、将蚂蚁分为探索蚁和确定蚁两种分工合作模式、保留父代最优路径3个方面对蚁群算法进行改进，并将其应用于农村垃圾车回收最优路径的确定中，从而减少运输路程。将改进后的蚁群算法与最大最小蚂蚁系统进行性能对比试验，结果显示，改进后的蚁群算法在迭代次数为132次时趋于稳定，且其最优值为623.157 9，均优于最大最小蚂蚁系统。该结果说明改进后的蚁群算法的寻找最优路径性能更优，可以利用其对农村垃圾回收路径进行确定，为农村垃圾治理领域提供一个新思路。

关键词：垃圾治理；蚁群算法；节约因子；回收路径

中图分类号：F799.3         文献标识码：A

文章编号：0439-8114（2024）03-0255-05

DOI：10.14088/j.cnki.issn0439-8114.2024.03.038 开放科学（资源服务）标识码（OSID）：

随着人们生活品质的提高，垃圾的产量也越来越高，而农村的垃圾处理问题频发，很多农村对垃圾治理不及时或方式不对，导致农村居民的生活质量下降［1，2］。国家对此非常重视，投入大量资金开展农村垃圾治理工作，但由于农村垃圾回收路径的规划模型不够完善，无法确定最短的垃圾回收路径，导致政府资金的浪费，因此探索一种可以确定农村垃圾回收最短路径的方法具有重要意义［3，4］。蚁群算法是一种根据蚂蚁运动演变而来的算法，其可以利用信息素的帮助确定最短路径［5］。但传统的蚁群算法收敛速度慢，确定最优路径的稳定性不高［6］。故将改进后的蚁群算法与农村垃圾回收路径模型相结合，确定农村垃圾回收的最短路径，从而降低农村垃圾治理的运输费用，为政府节省开支。

1 基于改进蚁群算法的农村垃圾治理模型构建

1.1 农村垃圾治理模型构建及相应路径优化算法

农村垃圾治理问题已成为广大农村的普遍问题，在农村垃圾治理中存在诸多问题［7］。为了更好地对农村垃圾进行治理并降低垃圾的运输成本，研究提出了一种农村垃圾回收路径（Rural garbage collection routing，RGCR）。该回收路径是以各小镇为单位，求得农村生活垃圾的总路程最小的转运路径，从而减少农村垃圾的运输成本。在一个小镇中，垃圾的回收过程如下，首先是多辆垃圾车离开车场，分别前往各乡村进行垃圾回收，当垃圾车回收的垃圾达到其最大载重量时，随即前往转运站进行倾倒垃圾，然后返回车场。RGCR如图1所示。

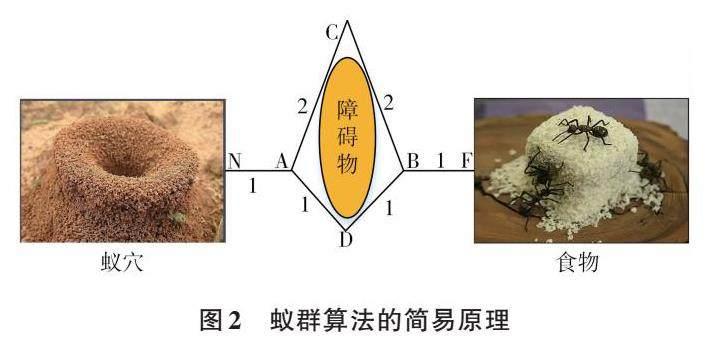
图1为某镇的垃圾回收路径图，从中可以看出，该镇共管辖7个乡村，利用2辆垃圾车对辖内7个乡村进行垃圾处理，2辆垃圾车从垃圾车场出发，对每个农村的垃圾进行回收，当垃圾车的垃圾收集量到达最大承载量后返回垃圾处理厂进行垃圾倾倒，然后返回垃圾车车场。在RGCR中包括垃圾车车场、农村、垃圾处理厂、垃圾车等要素。其中垃圾车车场既是垃圾车的出发位置也是其结束位置，而垃圾车是该路径中的主体，其主要作用是对垃圾进行运输。垃圾对应的是物流中的货物，具有重量及采集地点2个属性，其为垃圾车行驶路径选择的依据。农村为该回收路径中的服务对象，每个农村为1个垃圾采集点，且每个垃圾采集点能且只能被服务1次。垃圾转运站的主要功能是对垃圾进行倾倒。除此之外还有约束条件和目标函数，约束条件是指垃圾车在回收垃圾过程中需要满足的条件，而目标函数是指对路径问题进行求解的函数，研究选取车辆总行驶里程最短为目标函数对该路径问题进行求解。通过该垃圾回收模型找到车辆总行驶里程最短的路径即可节约垃圾运输成本。蚁群算法是一种最优化路径的方法，其基本原理与蚂蚁的运动相关［8］。具体内容为，蚂蚁会在其途径的道路上留下名为信息素的分泌物，蚂蚁之间可以通过信息素进行信息交流，蚂蚁在运动过程中会更喜欢沿着信息素浓度高的路径行走，因此该路径信息素浓度又会升高，从而形成正反馈现象［9］。在蚂蚁的路径行走正反馈现象形成一段时间后，会导致某条路径的信息素浓度远高于其他路径，此时大多数蚂蚁会在该路径上聚集，而该路径即为蚂蚁到食物源的最优路径［10］。蚁群算法的简易原理如图2所示。

如图2所示，蚁穴到食物之间存在NACBF和NADBF两条路径。假设在蚂蚁从蚁穴前往食物所在地的过程中速度相同且其在路过每一段路径时都会分泌相同量的信息素，则蚂蚁在图2的觅食过程具体描述如下所示。假定共有16只蚂蚁从蚁穴出发去食物F处，当过去1个时刻时，所有蚂蚁都移动至A处，此时由于AC、AD两条路径上均无信息素，故有8只蚂蚁选择AD、8只蚂蚁选择AC。在4个时刻后8只通过ADB路径的蚂蚁率先找到食物F并返回蚁穴，返回途径B点时因BC和BD的信息素浓度相同故选择BD和BC路径的蚂蚁数量相同。在8个时刻后，经过BDA返回蚁穴的4只蚂蚁回到蚁穴，其他的蚂蚁处于返回途中，其中BC中点处、AC中点处、D处各有4只蚂蚁。而在9个时刻后，返回到蚁穴的4只蚂蚁再次来到A处，此时AC和AD路径上的信息素数量分别为12和16，由于AD路径上的信息素含量较多，这4只蚂蚁将大概率选择AD路径前往食物F处。这将导致AD路径的信息素含量进一步增大，使得AD和AC路径上的信息素浓度差距越来越大，随着蚂蚁觅食过程时间的增长，最终会导致所有蚂蚁都聚集在NADBF这条较短的路径上。通过蚁群算法可以找到农村垃圾处理车运输的最短路径，从而减少运输成本。

1.2 蚁群算法的优化及其在RGCR中的应用

虽然传统的蚁群算法可以对最优路径进行求解，但其在实际的求解过程中仍存在收敛速度慢、优化能力不足的问题。为了更好地利用蚁群算法对农村垃圾回收最优路径进行求解，对蚁群算法进行了3个改进得到混合蚁群算法（Hybrid ant colony algorithm，HACA）。HACA的第一个改进是在蚁群算法的基础上利用节约算法思想引入节约因子[uij]，在研究提出的RGCR模型中节约因子的计算原理如图3所示。

图3a的过程为从车场派出2辆垃圾车前往[i]、[j]  2个农村进行垃圾回收，在垃圾回收后2辆垃圾车前往转运站倾倒垃圾，然后返回车场，图3b的过程为从车场派出1辆垃圾车前往[i]、[j] 2个农村进行垃圾回收，利用该路径的前提是垃圾车的承载量大于[i]、[j] 2个农村的垃圾总量。而节约因子其实就是图3b中的总里程数与图3a中总里程数的差值，其表达式如式（1）所示。

[uij=din+dn1+d1j-dij]      （1）

式（1）中，[n]为垃圾转运站；[i]和[j]分别为2个农村节点；[dij]表示2个农村节点之间的距离。最大最小蚂蚁系统（Max-min ant system，MMAS）通过只允许在最好的解中增加信息素来实现最优路径搜索。MMAS使用简单的机制限制了信息素的增强，有效避免了搜索的过早收敛。将[uij]应用于MMAS路径选择机制中，可以得到改进混合蚁群算法的路径选择机制公式如式（2）所示。

[j=argmaxs∈allowedkτis（t）αηisβμisγ，q≤q0pkij（t）=τij（t）αηijβμisγs∈allowedkτis（t）αηisβμisγ，                                    j∈allowedk，q>q0                       0，otherwise] （2）

式（2）中，[γ]为节约因子在路径选择过程中的重要程度；[k]为蚂蚁；[t]为蚂蚁访问城市节点[i]的时刻；[j]为蚂蚁[k]下一个需要访问的城市节点；[s]表示访问途中的城市节点；[η]表示启发式因子；[α]和[β]分别表示路径上的信息素浓度和启发信息的相对重要性。HACA的第二个改进之处为在蚂蚁进行食物搜寻时，将蚂蚁分为探索性搜寻和确定性搜寻2类，将1/5的蚂蚁用作探索性搜寻，剩余的蚂蚁用作确定性搜寻，通过2种搜寻方式相结合的方式，对发现最优解有所帮助。若蚂蚁为探索性搜寻蚂蚁，则按照随机比例规则对下一个农村节点进行选择，其选择公式如式（3）所示。

[pkij（t）=τij（t）αηijβμisγs∈allowedkτis（t）αηisβμisγ，j∈allowedk，q>q0        0，   otherwise]   （3）

式（3）中，[α]为信息素重要程度；[β]为启发信息重要程度。除此之外，HACA还选择保留一部分父代最优路径，通过将其与此次最优解相比较，在更优的路径中添加更多的信息素。这种方式不仅可以保留优良基因，还在一定程度上扩大了解的范围，减慢了算法的收敛速度。若算法此次最优解的长度为[Lbest]，次优解长度为[L]，父代最优解的长度为[Lfb]，当路径[（i，j）]在本次迭代最优解中时，信息素增加量表达式如式（4）所示。

[Δτij=0.6×1Lbest] （4）

若路径（i，j）不在本次迭代最优解中时，则信息素额外增量的公式如式（5）所示。

[Δτ*ij=Δτfbij，Lfb≤LbestΔτ′ij，Lfb>Lbest] （5）

式（5）中，[Δτfbij]为路径（i，j）在父代最优解中时的信息素增加量，其表达式如式（6）所示。

[Δτfbij=0.4×1Lfb] （6）

式（5）中，[Δτ′ij]为路径（i，j）在算法迭代最优解中时的信息素增加量，其表达式如式（7）所示。

[Δτ′ij=0.4×1L] （7）

最终通过式（8）所示的表达式对路径上的所有信息素进行更新，在更新结束后对信息素的浓度进行调整，然后确定是否结束迭代。

[τij（t+1）=（1-p）τij（t）+Δτij+Δτ*ij] （8）

式（8）中，[p]为信息素挥发系数。通过改进后的蚁群算法具有更好的收敛性和准确性，其对农村垃圾回收最优路径的求解具体过程如图4所示。

如图4所示，改进后的蚁群算法运行的第一步是对参数进行初始化，然后确定蚂蚁的编号，通过蚂蚁编号确定其是否为探索性蚂蚁，通过式（2）、式（3）分别对路径进行选择，若形成路径则继续下一步，若未形成则重新确定编号。未形成m条路径时，将蚂蚁编号加1再次进行输入，在形成m条路径后，对所有路径的长度排序并找出最短路径，将其与父代最优解长度进行对比，根据对比结果情况，利用式（4）至式（8）对路径上的信息素增加量进行计算，最后将信息素调整在上下限之内，确定是否迭代结束，若结束则输出路径最优解与对应路径，若未结束则继续进行算法。

2 农村垃圾治理模型仿真试验结果分析

为了对研究提出的HACA性能进行验证及对比，将其MMAS在2组算例中的测试结果进行比较。2组算例的具体内容如下所示。算例A中垃圾车的最大载重量为4 600 kg，节点共31个，1号节点为车场，31号节点为转运站，其他节点均为农村节点；算例B中垃圾车的最大载重量为180 kg，节点共51个，1号节点为车场，51号节点为转运站，其他节点均为农村节点。在测试算例A、B时，设置最大迭代次数200次；蚂蚁规模为30；[α=1]；[β=2]；[γ=1]；[q0=0.2]。研究将HACA和MMAS在算例A、B中运行10次，其结果对比如表1所示。

从表1中可以得到，在算例A中的10次运行结果中，HACA的最大值为669.631 7，低于MMAS的最大值702.217 5，且HACA的最小值为623.157 9，低于MMAS的最小值662.378 5；在算例B中的10次运行结果中，HACA的最大值为667.125 8，低于MMAS的最大值753.647 8，且HACA的最小值为619.356 4，低于MMAS的最小值668.247 9。该结果说明HACA搜寻到的最优解最小，说明其路径质量更优，也说明HACA搜寻最优解的性能优于MMAS。

除了对路径结果进行对比外，还对2种算法的收敛性进行对比，其中改进蚁群算法和最大最小蚂蚁算法在算例A、B中的最优解收敛性对比如图5、图6所示。

由图5可知，HACA在算例A中迭代次数为130次时最优值趋于稳定，且最优值稳定在650左右；而MMAS在算例A中在迭代次数为200次时还未趋于稳定，且数值在700～800附近波动。该结果说明，HACA在算例A中的收敛性优于MMAS，且最优值也优于MMAS，此结果也可以说明HACA搜寻最优路径的性能优于MMAS。

由图6可知，HACA在算例B中迭代次数为133次时最优值趋于稳定，且最优值稳定在650左右；而MMAS在算例B中在迭代次数为200次时还未趋于稳定，且数值在700～900附近波动。该结果说明，HACA在算例B中的收敛性优于MMAS，且最优值也优于MMAS，此结果也可以说明HACA搜寻最优路径的性能优于MMAS。通过上述结果可以得出HACA相较于MMAS可以更好地找到最优路径，且其更加稳定，利用该方式对农村垃圾回收路径进行确定，可以有效地减少运输成本。

3 小结

针对农村垃圾回收最短路径较难确定的问题，研究提出一种基于节约因子以及分工模式的改进蚁群算法，通过将该算法与农村垃圾回收路径模式相结合，可得到农村垃圾回收的最优路径。将优化后的HACA与MMAS进行仿真试验对比性能，结果显示，HACA在算例A中结果的最大值和最小值分别为669.631 7和623.157 9，HACA在算例B中结果的最大值和最小值分别为667.125 8和619.356 4；均低于MMAS，且HACA在迭代次数为132次时趋于稳定，且其最优值在650左右，而MMAS在迭代次数为200次时还未稳定。上述结果说明，进行优化后的蚁群算法HACA确定最优路径的性能明显优于MMAS，且其收敛速度也提高了，可以快速进行收敛，从而提高整体性能。也说明利用HACA可以更好地对农村垃圾回收最短路径进行精准确定，从而减少政府的运输成本。虽然研究提出的算法具有较高的性能，但在研究过程中，只针对镇转运进行了研究，建立的模型较单一，后续将会对数学模型进行完善，并对完善的数学模型中的蚁群算法进行改进。

参考文献：

［1］ 曲 青，董立波，赵 涛. 精准施策巧分类 垃圾治理成效显［J］. 环境卫生工程， 2022， 30（1）：90-93.

［2］ LI X R， BI F， HAN Z D， et al. Garbage source classification performance， impact factor， and management strategy in rural areas of China： A case study in Hangzhou［J］. Waste management， 2019， 89：313-321.

［3］ 屠 翰， 华永新， 徐 钢，等. 杭州市农村生活垃圾治理实践及问题对策研究［J］. 农业资源与环境学报， 2018， 35（3）：251-256.

［4］ MELLYANAWATY M，NAKAKOJI S，TATARA M，et al. Enrichment of thermophilic methanogenic microflora from mesophilic waste activated sludge for anaerobic digestion of garbage slurry［J］. Journal of bioscience and bioengineering， 2021， 132（6）：630-639.

［5］ KANSO B，KANSOU A，YASSINE A. Open Capacitated ARC routing problem by Hybridized Ant Colony Algorithm［J］. RAIRO-Operations research， 2021， 55（2）：639-652.

［6］ 陈 宇，王 彪. 基于改进蚁群算法的二维MUSIC多谱峰搜索研究［J］. 声学技术， 2021， 40（1）：128-133.

［7］ 李亚娟. “美丽乡村”下的农村生活垃圾治理影响因素研究［J］. 环境科学与管理， 2019， 44（7）：59-63.

［8］ 胡致远，王 征，杨 洋，等. 基于人工鱼群-蚁群算法的UUV三维全局路径规划［J］. 兵工学报， 2022， 43（7）：1676-1684.

［9］ 陈东宁，刘一丹，姚成玉，等. 多阶段自适应蝙蝠-蚁群混合群智能算法［J］. 机械工程学报， 2021， 57（6）：236-248.

［10］ SALEH A I，ELKASAS M S， HAMZA A A. Ant colony prediction by using sectorized diurnal mobility model for handover management in PCS networks［J］. Wireless networks， 2019， 25（2）：765-775.

收稿日期：2022-10-13

基金项目：陕西省2021年度政务公开第三方评估项目（SCZC2021-CS -1289/001）

作者简介：李 婷（1986-），女，陕西米脂人，讲师，在读硕士研究生，研究方向为社会治理、政务公开，（电话）13991182045（电子信箱）935742690@qq.com。