V2Si(n=8~17)团簇几何结构、稳定性及特性分析

李成刚 申梓刚 崔颍琦 田浩 丁艳丽 任保增

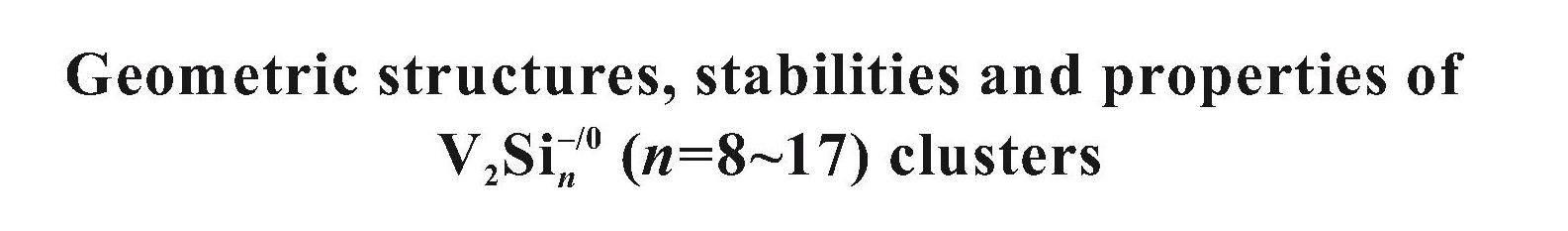
doi： 10.11835/j.issn.1000-582X.2022.128

收稿日期：2022-07-25

网络出版日期：2022-11-28

基金项目：国家自然科学基金资助项目（11904328，12104416）；郑州师范学院青年骨干教师培养计划（QNGG-211361）；郑州师范学院本科教学改革研究项目（JXGG-20773）；郑州师范学院优秀基层教学组织建设项目（物理与电子工程学院物理学教研室）资助。

Foundation：Supported by National Natural Science Foundation of China （11904328， 12104416）， Training Plan for Young Core Teachers in Zhengzhou Normal University （QNGG-211361）， Reform of Undergraduate Teaching in Zhengzhou Normal University （JXGG-20773）， and Basic Teaching Organization of Zhengzhou Normal University （Physic Teaching and Research Office in College of Physics and Electronic Engineering）.

作者简介：李成刚（1979—），男，博士，主要从事团簇的结构及物性研究，（E-mail）chenggangli@zznu.edu.cn。

通信作者：申梓刚，男，博士，教授，（E-mail）11134809@qq.com。

摘要：随着硅团簇研究的深入，过渡金属原子掺杂硅团簇的研究得到广泛关注。基于密度泛函理论，系统分析了钒原子掺杂硅团簇的几何结构、稳定性及特性。首先，基于粒子群优化算法的卡里普索结构预测程序，对（n=8～17）团簇的基态和亚稳态结构进行了系统搜索。B3LYP/6-311+G（d）水平下优化发现，基态结构中2个钒原子的掺杂引起了原硅团簇结构的重构；随着掺杂体系尺寸增大，2个钒原子（形成V-V键）逐渐被硅笼包裹。其次，以此结构为基础，通过分析平均键能、二阶能量差分和HOMO-LUMO能隙，研究了体系的稳定性。结果表明，团簇在各自体系中具有相对高的稳定性。此外，磁性分析发现，闭壳层V2Sin （n=8～17）体系的总自旋磁矩均为零，开壳层 （n=8～17）体系分别拥有1 μB的总磁矩。分析极化率发现，拥有最大的平均极化率，具有强的非线性光学效应。拟合得到的光电子能谱、红外和拉曼光谱为进一步的实验研究提供了理论支持。热力学特性分析表明，研究体系在热力学上是稳定的。随着温度升高，定容热容和标准熵逐渐增大；随着压强增大，标准熵逐渐减小。

关键词：卡里普索；几何结构；稳定性

中图分类号：O6          文献标志码：A               文章编号：1000-582X（2024）05-122-11

Geometric structures， stabilities and properties of V2Si （n=8～17） clusters

LI Chenggang1，2， SHEN Zigang1， CUI Yingqi1， TIAN Hao1， DING Yanli1， REN Baozeng2

（1. College of Physics and Electronic Engineering， Zhengzhou Normal University， Zhengzhou 450044， P. R. China; 2. School of Chemical Engineering and Energy， Zhengzhou University， Zhengzhou 450001， P. R. China）

Abstract： The study of silicon clusters has led to significant interest in transition metal atoms doped silicon clusters. In order to provide robust guidelines for future experimental and theoretical investigations of vanadium doped silicon nanomatrials， the geometric structures， stabilities and properties of  （n=8～17） clusters were systemically studied using density functional theory. Firstly， the lowest and lower lying energy structures of （n=8～17） clusters were globally predicted using the CALYPSO （crystal structure analysis by particle swarm optimization） searching method via the particle swarm optimization algorithm. Geometry optimization at the B3LYP/6-311+G（d） level revealed that two vanadium atoms tend to form V2 bonds encapsulated gradually into silicon cages with an increasing number of silicon atoms. Secondly， based on the lowest energy structures， calculations of the average binding energy， second order energy difference， and HOMO-LUMO gaps indicated that the  clusters exhibit higher stability， respectively. In addition， magnetic properties analyses revealed that the total magnetic moment is zero for the closed-shell structures of V2Sin （n=8～17） clusters; However， the open-shell structures of V2Sin （n=8～17） clusters have magnetic moments with values of 1 μB. Upon polarizability analysis，  clusters with the highest mean dipole polarizability possess stronger nonlinear optical properties. Furthermore， the simulated PES（photoelectron spectroscopy）， IR （infrared）， and Raman spectra can provide theoretical guidance for future experimental investigations. Finally， the lowest energy structures of V2Sin （n=8～17） clusters are stable thermodynamically. Moreover， the heat capacity at constant volume （Cv） increases with the increasing of temperature， and standard entropy （S） decreases with temperature increasing.

Keywords： CALYPSO; geometric structures; stabilities

位居第IVA族的硅原子sp2轨道杂化缺失，导致其存在大量悬挂键，使硅团簇的稳定性很差。大量的理论和实验研究发现，当非金属或金属原子掺杂硅团簇后，原有硅团簇的几何结构和性质发生了很大变化，如：提高了稳定性、提升了特性（如能级结构、电离势、几何结构和电子布局等）、改变了反应活性、改变了局域电子磁矩的分布等[1-5]。特别是具有空d轨道的过渡金属原子掺杂硅团簇，不仅可以填充硅团簇表面的空轨道，减少团簇表面的悬挂键数目，有效提高硅团簇的稳定性，而且产生具有高对称性的新颖构型，表现出诸多特殊物理化学特性。因此，此类掺杂体系引起了科研工作者的广泛关注。文献[6-8]报道了在实验中制备出过渡金属掺杂硅团簇。基于密度泛函理论，众多研究关注不同电荷下过渡金属原子（Sc、Ti、V、Cr、Mn、Fe、Co、Ni、Cu等）掺杂硅团簇的几何结构、稳定性和电子特性[9-12]。基于实验和密度泛函理论相结合，文献[13-14]报道了过渡金属（V、Mn、Ag）掺杂硅团簇的几何结构、电荷及HOMO-LUMO能隙。此外，对Cu、Cr、Ti、Co和Au等掺杂不同尺寸硅团簇的几何结构、稳定性和电子及磁学特性的研究发现，基态结构多呈现为过渡金属原子内包于硅团簇的笼式结构，如：、、TiSi12、CoSi10和AuSi12等[15-19]。

双原子掺杂硅团簇后的结构和电子特性会如何变化呢？在B3LYP/LANL2DZ水平下，Han等[20]对Mo2Sin（n=9～16）的几何结构，相对稳定性和电荷转移特性进行了研究。结果发现，随着体系尺寸的增大，Mo-Mo逐渐被硅笼包裹。Ji等[21]的研究表明，从n=10开始，Pd2Sin （n=9～16）团簇中的一个Pd原子也逐渐被硅笼包围。随后，中性和带电Rh2Sin （n=1～10）团簇的电子特性[22]，M2Si8 （M=Ti-Zn）团簇的几何结构、稳定性和磁性[23-24]，中性和阴性T2Sin （T=Cr， Mn， Fe， Co， Ni; n=1～8）团簇的磁性也逐步被研究[25-26]。特别是Xu等[27-28]利用实验的光电子能谱和密度泛函理论，对2个V原子掺杂硅团簇的结构和特性进行了系统研究。结果发现，2个V原子的掺杂使得原硅团簇的结构产生了重构。其中，团簇拥有高对称性的D3d点群对称结构，中V-V键表现出较强的稳定性。此外，Lu等[29]利用密度泛函理论研究了 （n<12）结构的增长模式，拟合出了阴离子团簇的光电子能谱，讨论了体系的相对稳定性和电荷转移特点，发现了中性和阴性V2Si10拥有相对高的稳定性。在课题组前期工作中，对V2Sin （n=1～10）团簇的结构、稳定性和电子特性进行了深入研究[30]。结果发现，n=1～8时，2个V原子占据表面位置，n=9～10时，其中一个V原子被硅笼包裹，V2Si6团簇具有相对高的稳定性，电荷从V向Si原子转移，V和Si原子之间存在强的sp轨道杂化。

在前期工作基础上，笔者增大了研究对象的尺寸范围，同时考虑电荷影响，利用卡里普索结构预测程序和密度泛函理论，搜索了不同电荷下V2Sin （n=8～17）团簇的基态和亚稳态结构。基于基态结构，分析了不同尺寸下团簇的相对稳定性，研究了掺杂体系的磁性和极化率，拟合出了光电子能谱、红外和拉曼光谱，讨论了体系的热力学特性，以及温度、压强对热力学参数的影响。

1 计算方法

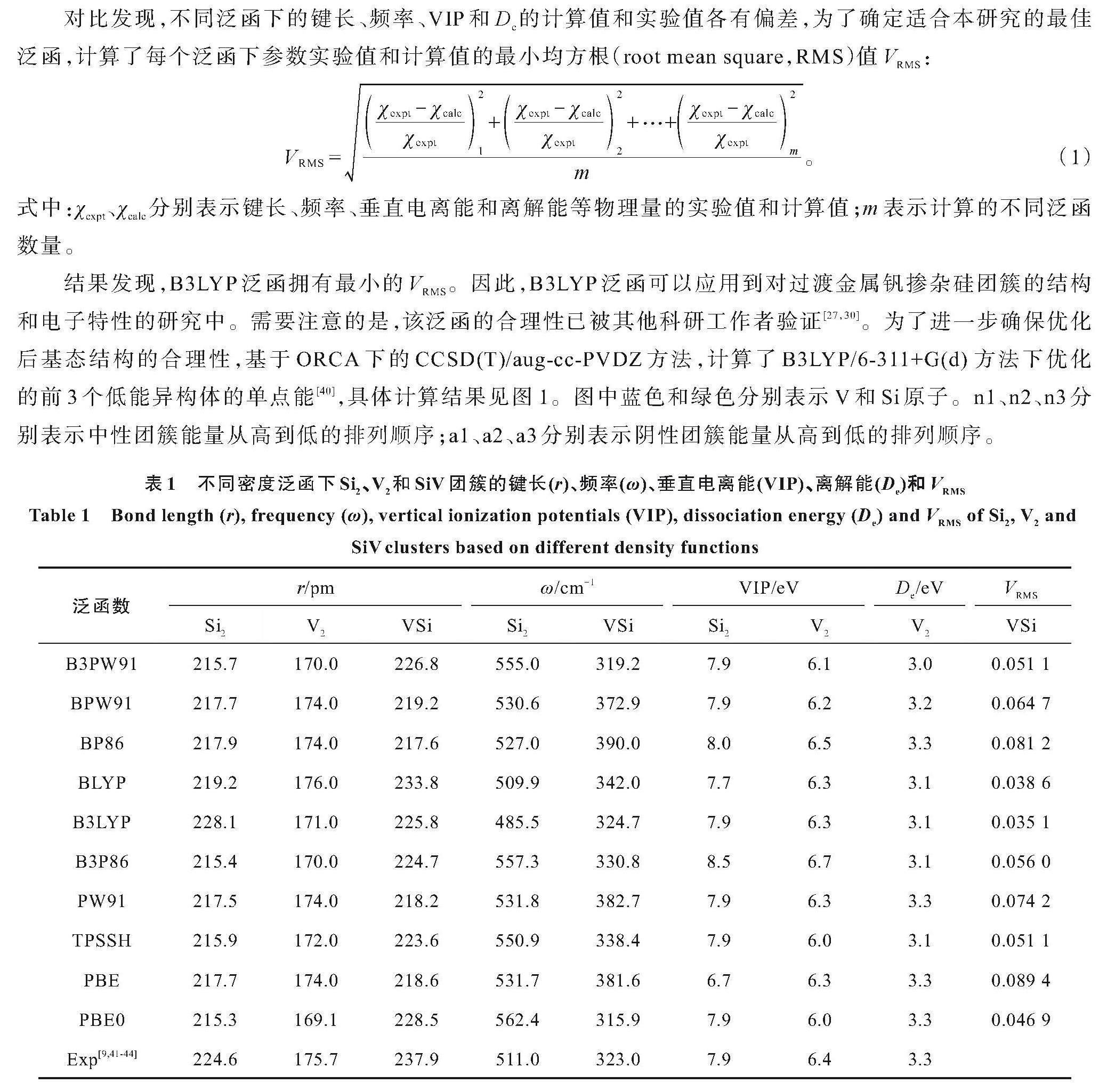
本研究中的计算均在Gaussian 09程序下进行[31]，对于 （n=8～17）团簇结构的优化和特性的计算均采用B3LYP泛函，对于V和Si原子均采用6-311+G（d）基组。其中，对研究对象初始结构的搜索中，引入了卡里普索（crystal structure analysis by particle swarm optimization，CALYPSO）结构预测程序[32-34]。该方法采用了基于对称性限制的随机结构产生技术、成键特征矩阵的结构相似性判断技术和粒子群优化算法的结构演化技术等，以保证对团簇势能面的有效探索，具体的描述可以参阅相关已报道的文献[35-37]。具体搜索过程如下：首先，基于不同自旋多重度（1、3、5、7;2、4、6、8），利用PBE/3-21G水平对初始结构进行搜索，通过设置种群数和演化的代数参量，即可得到相应数量的初始结构数（总结构数=种群数×代数）。其次，从一定数量初始结构中筛选出能量差超过0.3 eV的50个结构，再利用高精度的B3LYP泛函和6-311+G（d）基组对其进行优化[38-39]，进而确定体系的基态和亚稳态结构。此外，为了验证B3LYP泛函的合理性，分别计算了不同泛函（B3PW91、BPW91、BP86、BLYP、B3LYP、B3P86、PW91、TPSSH、PBE、PBE0）下Si2、V2和SiV团簇的键长、频率、垂直电离能（vertical ionization potentials，VIP）和离解能（De），计算结果见表1。

对比发现，不同泛函下的键长、频率、VIP和De的计算值和实验值各有偏差，为了确定适合本研究的最佳泛函，计算了每个泛函下参数实验值和计算值的最小均方根（root mean square，RMS）值VRMS：

。    （1）

式中：χexpt、χcalc分别表示键长、频率、垂直电离能和离解能等物理量的实验值和计算值；m表示计算的不同泛函数量。

结果发现，B3LYP泛函拥有最小的VRMS。因此，B3LYP泛函可以应用到对过渡金属钒掺杂硅团簇的结构和电子特性的研究中。需要注意的是，该泛函的合理性已被其他科研工作者验证[27，30]。为了进一步确保优化后基态结构的合理性，基于ORCA下的CCSD（T）/aug-cc-PVDZ方法，计算了B3LYP/6-311+G（d） 方法下优化的前3个低能异构体的单点能[40]，具体计算结果见图1。图中蓝色和绿色分别表示V和Si原子。n1、n2、n3分别表示中性团簇能量从高到低的排列顺序；a1、a2、a3分别表示阴性团簇能量从高到低的排列顺序。

2 结果讨论

2.1（n=8～17）团簇几何结构

基于上节中的卡利普索结构预测程序，在B3LYP/6-311+G（d）水平下对 （n=8～17）团簇的几何结构进行了优化，优化后的基态和亚稳态结构见图1。首先，对比B3LYP/6-311+G（d）和CCSD（T）/aug-cc-PVDZ//B3LYP/6-311+G（d）水平下的能量发现，虽然在2种方法下相对能量排序有变化，但基态结构保持着最大能量值，说明采用B3LYP/6-311+G（d）方法优化得到的基态结构是合理的。其次，对比文献[29]的研究结果发现，本研究中优化的V2Si8、V2Si10、和基态结构与其完全相同。然而，V2Si9、V2Si11、、和基态结构同本文优化后基态结构不同，为了确保上述基态结构的合理性，基于B3LYP/6-311+G（d）方法，对文献[29]中V2Si9、V2Si11、、和基态结构进行了重新优化，结果发现，文献[29]中V2Si9（0.89 eV）、V2Si11（0.43 eV）、（0.23 eV）、（0.24 eV）和（0.12 eV）的基态结构能量均高于本研究中优化后的基态结构能量。此外，所有掺杂体系基态呈笼式结构，且随着掺杂体系尺寸增大，掺杂的2个钒原子逐渐从笼子表面进入内部。

2.2 相对稳定性

确定了 （n=8～17）团簇的基态构型后，通过计算平均键能（average binding energy）Eb、二阶能量差分（second order energy difference）Δ2E和HOMO-LUMO能隙（HOMO-LUMO energy gap）Egap，对体系的稳定性进行了研究，对应的计算公式如下

（2）

式中，E为对应原子的能量。

图2给出了Eb、Δ2E和Egap随尺寸变化的关系。V2Sin （n=8～10）团簇的Eb小于对应纯硅团簇的Eb，说明掺杂体系的稳定性小于纯硅团簇的稳定性；当n≥11时，掺杂体系的稳定性大于对应纯硅团簇的稳定性。对于阴离子体系，当n≥12时，掺杂体系的稳定性大于对应纯硅团簇的稳定性；当n＜12时，掺杂体系的稳定性弱于对应纯硅团簇的稳定性。（n=8～17）团簇的Δ2E随尺寸增大呈现奇偶变化的规律，当n为偶数时表现出相对高的稳定性。V2Sin （n=8～17）团簇的Egap随尺寸的增大先增大后减小，在n=10具有最大值。对于阴离子体系，其Egap也表现出奇偶变化的规律。结合Δ2E和Egap的分析可得，团簇在各自体系中具有相对高的稳定性。

2.3 磁性分析

本节中，基于B3LYP泛函和6-311+G（d）全电子基组对磁学特性进行了分析讨论。轨道的电子占据数由Mulliken布局分析得到，磁矩可由自旋向上态（α）和自旋向下态（β）电子占据数之差获得。对于V2Sin （n=8～17）团簇，布局分析发现，所有尺寸的团簇都没有单电子占据分子轨道，每个团簇（n=8～17）拥有的分子轨道数分别为79、88、93、100、107、114、121、128、135和142，每个轨道上填充2个电子，即所有电子两两配对，电子轨道排布形成闭壳层，总自旋磁矩为零，即发生了“磁矩猝灭”现象。因此，V2Sin （n=8～17）团簇不具有磁性。对于 （n=8～17）体系，从其轨道布局可以发现，电子占据不同的α和β轨道，对应n=8～17，α和β轨道电子占据数分别为（80， 79）（87， 86）（94， 93）（101， 100）（108， 107）（115， 114）（122， 121）（129， 128）（136， 135）和（143， 142）。对比发现，电子在α轨道上的占据数比在β轨道上的多了一个，每个轨道对应一个玻尔磁子。因此，（n=8～17）体系分别具有1 μB的总磁矩。图3显示了（n=8～17）体系中V和Si原子的局域磁矩。整体来看，和中V原子的局域磁矩和Si原子的局域磁矩几乎相等，其他尺寸下，V原子的局域磁矩均大于Si原子的局域磁矩。

2.4 极化率

为了考查（n=8～17）团簇对外场的响应，计算了平均极化率和各向异性极化率Δα，公式为

（3）

式中：N为团簇的总原子数（团簇的尺寸）；、、、、和分别为张量对角元，具体计算结果见表2。从中发现，和团簇在各自体系中拥有最大和最小的平均极化率，说明团簇的电子结构相对稳定性差，容易被外加场极化，非线性光学效应强。团簇的相对稳定性强，最不容易被外加场极化，非线性光学效应弱。对于各项异性极化率，和V2Si17团簇各向异性极化率最大，说明对外场的各向异性响应较强；和V2Si10团簇各向异性极化率最小，说明对外场的各向异性响应最弱。

2.5 光电子能谱、红外、拉曼光谱

利用Multiwfn软件拟合出了（n=8～17）团簇的光电子能谱（图4）[45]。

根据搜索得到的基态结构，计算拟合出了（n=8～17）团簇的红外和拉曼光谱（图5）。

体系的红外和拉曼光谱拥有多个振动峰，其特征峰主要集中在低频区0～550 cm-1，而且不同结构对应不同的振动频率和强度，其区别主要由结构特征的不同所造成。此外，通过理论模拟对各团簇光谱的振动模式进行了归属分析。中性体系的红外光谱中，V2Si8团簇的红外谱在整个频段上都有峰值分散出现，其最强振动峰位于480 cm-1处，归属于3B-4B-8B和4B-5B-6B原子的伸缩振动。对于V2Si9团簇，位于159 cm-1处的最强振动峰归属于3B-5B-6B-7B-8B-9B-10B原子和2个钒原子的摇摆振动。当n=10，11时，442 cm-1和279 cm-1处的最强振动峰归属于2个钒原子沿V-V键的伸缩振动。V2Si12、V2Si13和V2Si14团簇中，最强振动峰（295 cm-1、297 cm-1和273 cm-1）归属于整个结构骨架以V-V键为对称中心的左右摇摆振动。对于V2Si15团簇，297 cm-1处的最强振动峰归属于所有硅原子在2个钒原子带动下摇摆振动。V2Si16和V2Si17团簇中，最强振动峰（218 cm-1和174 cm-1）归属于所有硅原子在2个钒原子带动下的左右摇摆振动。对于阴性团簇，由于基态结构的不同，其红外光谱中最强振动峰不同于中性团簇最强振动峰的振动模式。对比发现，除了团簇最强振动峰（435 cm-1）归属于伸缩振动模式外，其他尺寸团簇的最强振动峰（134、416、257、277、283、267、267、273 cm-1）都归属于摇摆振动模式。对于拉曼光谱，和红外光谱近似，随着团簇尺寸的增大，最强特征峰逐渐向低频方向偏移。中性团簇拉曼光谱特征峰（420～240 cm-1）归属于2个V和Si原子一起的呼吸振动模式。阴性团簇拉曼光谱最强特征峰对应的频率在280～365 cm-1，其最强特征峰归属于所有原子的呼吸振动模式。综上可见，（n=8～17）团簇的红外和拉曼活性在0～550 cm-1具有峰值分布，因而在整个频段内都表现较好。而且，随着团簇尺寸的增大，红外和拉曼谱的最强特征峰逐渐向低频方向移动。同时，中间尺寸的红外和拉曼谱的峰相对较少，小尺寸和大尺寸（n=8～17）团簇的红外和拉曼活性较好。此外，红外和拉曼的最强振动峰主要以摇摆振动模式为主，伸缩振动模式较少。通过对（n=8～17）团簇结构红外和拉曼光谱的分析比较，可以找出其特征吸收峰的振动归属，为此类团簇的实验合成和表征提供理论参考。

2.6 热力学性质

标准生成焓是衡量其热力学稳定性的一个重要参数，当标准生成焓为负值时，说明反应过程是放热反应，热力学上是稳定的。在标准大气压和温度下，计算了 （n=8～17）团簇的标准生成焓。

。    （4）

计算结果如表3所示。所有体系的均为负值，说明生成团簇都是放热反应，热力学上都是稳定的。而且，V2Sin的稳定性强于，同时，随着团簇尺寸的增大，稳定性逐渐提高。

为了探究温度和压强对热力学参数定容热容Cv（单位：J/（mol·K））和标准熵S（单位：J/（mol·K））的影响，分别计算了不同温度下的热力学参数，具体计算结果见图6。首先，不同温度（100、200、300、400、500、600、700、800 K）下，定容热容Cv 随着温度T的升高而增大，二者之间存在近似二次函数关系。标准熵S随着温度T的升高增大，二者之间存在近似线性关系。随着温度的升高，热力学参数均增大，主要是分子振动的贡献随温度升高而增加。同时，Cv和S的增加幅度随温度增加而减小。

以V2Si8和为例，Cv和T之间的函数关系如下：

（5）

式中，R2表示测定系数。

S和T之间的函数关系如下：

（6）

计算了不同大气压（0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8 MPa）下，压强P和标准熵S之间的关系。从图7可以发现，随着P增大，S逐渐减小，二者之间存在近似线性关系。以V2Si8和为例，压强P和标准熵S之间的函数关系如下。

（7）

3 结  论

运用卡里普索结构预测程序和密度泛函理论，在B3LYP/6-311+G（d）水平下，系统研究了 （n=8～17）团簇的几何结构、稳定性和电子、光谱和热力学特性。结构搜索发现，掺杂体系呈现笼式结构，对于小尺寸体系，一个V原子位于表面，另一个V原子位于笼的内部；随着体系的增大，2个V原子逐渐被硅笼包裹。V2Sin （n≥11）团簇的稳定性大于对应纯硅团簇的稳定性； （n≥12）团簇的稳定性大于对应纯硅团簇的稳定性。分析平均键能、二阶差分能和HOMO-LUMO能隙发现，团簇在各自体系中具有相对高的稳定性。磁性分析发现，由于α和β的电子数目相同，闭壳层V2Sin （n=8～17）体系的总自旋磁矩均为零。对于开壳层 （n=8～17）体系，由于电子占据不同的α和β轨道，使得每个体系分别具有1 μB的总磁矩。极化率分析发现，易被外加场极化的拥有最大的平均极化率，具有强的非线性光学效应；非线性光学效应弱的团簇具有最小的平均极化率。热力学性质分析表明，研究体系在热力学上都是稳定的。随着温度的升高，定容热容和标准熵逐渐增大；随着压强的增大，标准熵逐渐减小。温度和定容热容之间存在近似二次函数关系，温度与压强和定容热容之间存在近似线性关系。

参考文献

［1］  Zhao Y R， Bai T T， Jia L N， et al. Probing the structural and electronic properties of neutral and anionic lanthanum-doped silicon clusters[J]. The Journal of Physical Chemistry C， 2019， 123（47）： 28561-28568.

［2］  Khanna V， Singh R， Claes P， et al. Evolution of vibrational spectra in the manganese-silicon clusters Mn2Sin， n = 10， 12， and 13， and cationic[Mn2Si13]+[J]. The Journal of Physical Chemistry A， 2022， 126（10）： 1617-1626.

［3］  石胜云， 温良英， 曹娇， 等. CO和Cl2在TiO2（110）表面的吸附行为[J]. 重庆大学学报， 2019， 42（8）： 50-58.

Shi S Y， Wen L Y， Cao J， et al. Adsorption of both CO and Cl2 on TiO2（110） surface[J]. Journal of Chongqing University， 2019， 42（8）： 50-58.（in Chinese）

［4］  Zhu B C， Zhang S， Zeng L. The effect of silicon doping on the geometrical structures， stability， and electronic and spectral properties of magnesium clusters： DFT study of SiMgn （n = 1-12） clusters[J]. International Journal of Quantum Chemistry， 2020， 120（10）： e26143.

［5］  柳杨璐， 刘婷婷， 潘复生. 基于第一性原理的镁合金合金相及固溶体研究进展[J]. 重庆大学学报， 2018， 41（10）： 30-44.

Liu Y L， Liu T T， Pan F S. Research progress on intermetallic compounds and solid solutions of Mg alloys based on first-principles calculation[J]. Journal of Chongqing University， 2018， 41（10）： 30-44.（in Chinese）

［6］  Scherer J J， Paul J B， Collier C P. Cavity ringdown laser absorption spectroscopy and time-of-flight mass spectroscopy of jet-cooled copper silicides[J]. The Journal of Chemical Physics， 1995， 102： 5190.

［7］  Hiura H， Miyazaki T， Kanayama T. Formation of metal-encapsulating Si cage clusters[J]. Physical Review Letters， 2001， 86（9）： 1733-1736.

［8］  Xiao C Y， Hagelberg F， Lester W A. Geometric， energetic， and bonding properties of neutral and charged copper-doped silicon clusters[J]. Physical Review B， 2002， 66（7）： 075425.

［9］  Guo L J， Zhao G F， Gu Y Z， et al. Density functional investigation of metal-silicon cage clusters MSin （M=Sc， Ti， V， Cr， Mn， Fe， Co， Ni， Cu， Zn; n=8-16） [J]. Physical Review B， 2008， 77： 195417.

［10］  Kawamura H， Kumar V， Kawazoe Y. Growth， magic behavior， and electronic and vibrational properties of Cr-doped Si clusters[J]. Physical Review B， 2004， 70（24）： 245433.

［11］  Kawamura H， Kumar V， Kawazoe Y. Growth behavior of metal-doped silicon clusters SinM （M=Ti， Zr， Hf; n=8-16） [J]. Physical Review B， 2005， 71： 075423.

［12］  Torres M B， Fernandez E M， Balbas C， Theoretical study of isoelectronic SinM clsuter （M=Sc–， Ti， V+; n=14-18） [J]. Physical Review B， 2007， 75： 205425

［13］  Li Y J， Lyon J T， Woodham A P， et al. The geometric structure of silver-doped silicon clusters[J]. ChemPhysChem， 2014， 15（2）： 328-336.

［14］  Claes P， Ngan V T， Haertelt M， et al. The structures of neutral transition metal doped silicon clusters， SinX （n=6-9; X=V， Mn） [J]. The Journal of Chemical Physics， 2013， 138： 194301.

［15］  Guo L J， Liu X， Zhao G F. Computational investigation of TiSi （=2-15） clusters by the density-functional theory[J].The Journal of Chemical Physics， 2007， 126： 234704.

［16］  Wang J G， Zhao J J， Ma L， et al. Structure and magnetic properties of cobalt doped Sin （n=2-14） clusters[J]. Physics Letters A， 2007， 367（4/5）： 335-344.

［17］  Wang J， Liu Y， Li Y C. Au@Sin： growth behavior， stability and electronic structure[J]. Physics Letters A， 2010， 374（27）： 2736-2742.

［18］  Xu H G， Wu M M， Zhang Z G， et al. Photoelectron spectroscopy and density functional calculations of CuSi （n=4-18） clusters[J]. The Journal of Chemical Physics， 2012， 136： 104308.

［19］  Kong X Y， Xu H G， Zheng W J. Structures and magnetic properties of CrSi （n=3-12） clusters： photoelectron spectroscopy and density functional calculations[J]. The Journal of Chemical Physics， 2012， 137（6）： 064307.

［20］  Han J G， Zhao R N， Duan Y H. Geometries， stabilities， and growth patterns of the bimetal Mo2-doped Sin （n=9-16） clusters： a density functional investigation[J]. The Journal of Physical Chemistry A， 2007， 111（11）： 2148-2155.

［21］  Ji X X， Li J， Wang C， et al. Geometries， stabilities and electronic properties of small sized Pd2-doped Sin （n=1-11） clusters[J]. Molecular Physics， 2015， 113（22）： 3567-3577.

［22］  Zhang S， Zhang Y， Yang X Q， et al. Systematic theoretical investigation of structures， stabilities， and electronic properties of rhodium-doped silicon clusters： Rh2Si （n=1-10; q=0， ±1） [J]. Journal of Materials Science， 2015， 50（18）： 6180-6196.

［23］  Ji W X， Luo C L. Structures， magnetic properties， and electronic counting rule of metals-encapsulated cage-like M2Si18 （M=Ti-Zn） clusters[J]. International Journal of Quantum Chemistry， 2012， 112（12）： 2525-2531.

［24］  Ji W X， Luo C L. Density-functional investigation of hexagonal prism transition-metal-encapsulated cage M2Si18 （M=Sc-Zn） clusters[J]. Modelling and Simulation in Materials Science and Engineering， 2010， 18（2）： 025011.

［25］  Robles R， Khanna S N， Castleman A W Jr. Stability and magnetic properties of T2Sin （T=Cr， Mn， 1≤n≤8） clusters[J]. Physical Review B， 2008， 77（23）： 235441.

［26］  Robles R， Khanna S N. Stable T2Sin （T=Fe， Co， Ni， 1≤n≤8） cluster motifs[J]. The Journal of Chemical Physics， 2009， 130（16）： 164313.

［27］  Xu H G， Zhang Z G， Feng Y， et al. Vanadium-doped small silicon clusters： photoelectron spectroscopy and density-functional calculations[J]. Chemical Physics Letters， 2010， 487（4/5/6）： 204-208.

［28］  Xu H G， Kong X Y， Deng X J， et al. Smallest fullerene-like silicon cage stabilized by a V2 unit[J]. The Journal of Chemical Physics， 2014， 140（2）： 024308.

［29］  Lu J， Lu Q H， Li X J. Study on the growth patterns and simulated photoelectron spectroscopy of double vanadium atoms doped silicon clusters V2Sin （n≤ 12） and their anions[J]. Molecular Physics， 2021， 119（7）： e1864042.

［30］  Li C G， Chen W G， Cui Y Q， et al. Structures， stabilities and electronic properties of the bimetal V2-doped Sin （n=1-10） clusters： a density functional investigation[J]. The European Physical Journal D， 2020， 74（6）： 111.

［31］  Frisch G M J， Trucks W， Schlegel H， et al. Gaussian 09， revision A. 1; Gaussian[M]. New York： Gaussian Incorporated， 2009.

［32］  Wang Y C， Lv J， Zhu L， et al. Crystal structure prediction via particle-swarm optimization[J]. Physical Review B， 2010， 82（9）： 094116.

［33］  Wang Y C， Lv J， Zhu L， et al. CALYPSO： a method for crystal structure prediction[J]. Computer Physics Communications， 2012， 183（10）： 2063-2070.

［34］  Wang Y C， Miao M S， Lv J， et al. An effective structure prediction method for layered materials based on 2D particle swarm optimization algorithm[J]. Journal of Chemical Physics， 2012， 137（22）： 224108.

［35］  Li C G， Cui Y Q， Tian H， et al. Quantum chemistry study on the structures and electronic properties of bimetallic Ca2-doped magnesium Ca2Mgn （n=1-15） clusters[J]. Nanomaterials， 2022， 12（10）： 1654.

［36］  Li C G， Li H J， Cui Y Q， et al. A density functional investigation on the structures， electronic， spectral and fluxional properties of  cluster[J]. Journal of Molecular Liquids， 2021， 339： 116764.

［37］  Li C G， Cui Y Q， Li J X， et al. Probing the structural， electronic and spectral properties of a  cluster[J]. Molecular Physics， 2021， 119（10）： 1910744.

［38］  Becke A D. Density-functional thermochemistry. III： the role of exact exchange[J]. Journal of chemical physics， 1993， 98（7）： 5648-5652.

［39］  Krishnan R， Binkley J S， Seeger R， et al. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions[J]. The Journal of Chemical Physics，1980， 72（1）： 650-654.

［40］  Neese F. The ORCA program system[J]. WIREs Computational Molecular Science， 2012， 2（1）：73-78.

［41］  Spain E M， Behm J M， Morse M D. The 846 nm A' 3Σ←X 3Σ band system of jet-cooled V2[J]. The Journal of Chemical Physics， 1992， 96（4）： 2511-2516.

［42］  Winstead C B， Paukstis S J， Gole J L. Spectroscopy of the H3Σ electronic state of Si2 using a combined laser vaporization-REMPI and oven-based LIF study[J]. Journal of Molecular Spectroscopy， 1995， 173（2）： 311-332.

［43］  Huber K P， Herzberg G. Constants of diatomic molecules[M]// Molecular Spectra and Molecular Structure. Boston， MA： Springer， 1979： 8-689.

［44］  James A M， Kowalczyk P， Langlois E， et al. Resonant two photon ionization spectroscopy of the molecules V2， VNb， and Nb2[J].Journal of Chemical Physics， 1994， 101（6）： 4485-4495.

［45］  Lu T， Chen F W. Multiwfn： a multifunctional wavefunction analyzer[J]. Journal of Computational Chemistry， 2012， 33（5）： 580-592.

（编辑  吕建斌）