爆破振动对临近尾矿坝的影响分析
刘梦 王晶晶 蒙萌 史秋波


[关键词]爆破振动;尾矿坝;数值模拟;稳定计算
0引言
随着国民经济水平的不断提高,能源需求明显增加,采矿行业得到了飞速发展。露天矿山开采利用的规模也不断扩大。因资源、环境、征地等因素的影响,采区面积逐渐扩大,爆破振动对临近尾矿坝带来的影响和产生的问题也愈加难以忽视。
爆破作业是露天矿山开采过程中不可或缺的一环,具有持续时间长、频率高、爆破药量大等特点,但也可能给周围环境带来潜在的危害。而尾矿坝是矿山建(构)筑物中的重大危险源,具有高危性。爆破可能使临近尾矿坝液化、失稳甚至溃坝。因此,深入研究爆破作业产生的振动对附近尾矿坝的影响,对于确保矿山安全至关重要。
针对这一研究课题,许多学者通过现场监测或数值模拟的方法做了分析,以此研究爆破振动对尾矿坝的影响。何方维等研究了露天采场爆破与尾矿库的交互影响:柴衡山等针对临近尾矿坝爆破的现象,根据萨道夫斯基经验公式对不同振速控制标准下的安全距离与允许最大起爆药量进行了估算。
但是,上述研究中也存在一定的不足。首先,因GB6722-2014《爆破安全规程》中爆破振动安全允许质点振速中未明确保护对象为尾矿坝时的允许标准值,各学者选取的最大允许振速并不相同。其次,GB39496-2020《尾矿库安全规程》中对特殊运行工况的抗滑稳定最小安全系数有相应要求,爆破方案设计中应对尾矿坝进行抗滑稳定性计算。若直接选取现场监测的振动数据作为特殊工况的输入载荷进行稳定计算,只能判定经历当前爆破后的尾矿坝状态,无法在设计阶段判断尾矿坝的稳定性。
针对上述不足,本文中,提出萨道夫斯基公式与数值模拟相结合的方法,分析爆破振动对临近尾矿坝的影响。首先,在临近尾矿坝附近采用小孔装药试验的方式得到相应的振速数据,并进行回归分析,确定萨道夫斯基公式中的参数:再利用此公式计算出爆破设计方案中的最大振速:然后,将试验采集的振速信号进行希尔伯特一黄转换(HHT)后得到频谱,初步判定最大振速是否满足要求;最后,将振速信号数值微分转化成加速度信号,并作为输入源输入到数值模型中,分析相应爆破参数下的尾矿坝稳定性和坝体的振动响应。通过尾矿坝稳定性的变化趋势,确定尾矿坝安全允许质点速度,并判断坝体峰值振速是否满足要求。
1实例分析
1.1工程简介
某公司计划对采区东北侧的一山梁边坡进行爆破削坡处理。该公司所属尾矿坝坝脚距待削坡的山梁直线距离为340m,山梁顶部高于坝脚约32m。此区域主要地层为太古界单塔子群白庙组(Arb)和第四系上更新统(Q3)、全新统(Q4)。主要岩性为角闪斜长片麻岩、斜长角闪岩,片麻理产状为:北东倾向,倾角30°-50°。
该尾矿坝坝顶标高约为747.2m。初期坝为土石坝,坝高10m;堆积坝为尾砂堆积而成的坝,坝高39m。总坝高为49m,堆存尾砂量约为50万m3,等别为四等库。坝内已无水。
在爆破设计初步方案中,采用中深孔微差爆破,孔径250mm,钻孔深度为12.0m,超深为2.0m,并采用双排孔交错布置的方式进行爆破作业。孔网参数为:孔距6.1m,排距5.3m,炸药单耗0.79kg/m3,单段最大装药量为255kg。采用连续装药,每孔装药量255g,炮孔填塞长度5.5m。采用导爆管雷管分段起爆系统。孔内外毫秒起爆网路中,孔内用高段位雷管,孔外用低段位雷管。台阶推进方向由西至东。
1.2试验方案
为研究爆破振动对临近尾矿坝的影响,进行5组爆破试验,如表1所示。5组爆破试验的爆心距、单段最大装药量均不同,其余爆破参数与采区爆破方案一致。单段装药量分别为10、20、30、40 kg和50kg。采用TC-4850型爆破测振仪(成都中科测控公司),使用石膏将传感器和尾矿坝稳定土层接触部分粘贴牢固。共布置5个测点。其中,测点1#在初期坝脚外约23m处:测点2#在初期坝坝脚处;测点3#位于初期坝坝顶:测点4#位于堆积坝标高730m平台;测点5#位于堆积坝坝顶。
1.3试验结果
测得的典型振速(试验I中的测点1#,尾矿坝主沟的方向)曲线如图l所示。不同测点的最大振速结果见表1。
式中:u为质点峰值振速;K为与爆破作用条件、地形地质条件有关的爆破振动系数:a为与爆区至测点间的地形、地质条件有关的爆破振动衰减指数;Q为最大单段药量;R为测点至爆源的距离。
将表1中的测试数据代人式(1),进行线性拟合,最终可得振动系数K=214.93、振动衰减指数a=1.716。拟合结果如图2所示。
根据拟合出的萨道夫斯基公式计算,爆破设计方案下尾矿坝测点1#的峰值振速为0.261cm/s、测点2#的峰值振速为0.232cm/s。
分析各振速的频谱,得到爆破振动主频f在0~50Hz之间。在GB6722-2014《爆破安全规程》中,建议露天深孔爆破选取的振动主频在10~60Hz之间,二者基本一致。典型振速曲线的频谱如图3所示。
参照GB6722-2014《爆破安全规程》中规定的各类保护对象最小的安全允许质点速度,在振动主频为10Hz
2数值模拟
2.1计算模型
采用Midas GTS建立三维模型。计算模型剖面以初期坝外壩脚为计算原点(0.0,0)。主沟方向为y向,主沟内侧为正,y向最小处为测点1#位置;x向以面向坝外左侧为正,x向最小处距堆积坝右侧坝顶约为13m;z向以向上为正,z向最小处比初期坝坝脚低约24m。初期坝坝高10m,总坝高为49m。库内浸润线埋深约为5m。模型总长度为300m,宽度200m,高度373m;共有73944个单元,188698个节点。计算模型见图4。图4中,给出了尾矿坝各层的岩土情沉。
2.2计算方法
采用Mohr-Coulomb本构模型对尾矿坝进行稳定性分析,稳定计算方法为强度折减法。动力计算中,爆破载荷为放大后的加速度曲线,分析方法为时程分析法。
坝体抗滑稳定系数判断标准是坝体材料进入塑性阶段,且塑性区域贯通坝体。
2.3岩体力学物理指标
根据岩土工程勘察,尾矿坝各层的岩土技术参数如表2所示。
2.4边界条件及爆破振动载荷
模型底部为固定边界,顶部为自由边界。静力计算时,周边为弹性边界,弹性边界用曲面弹簧定义。动力计算时,边界为无反射边界,具体系数计算公式如下:
5组试验方案与爆破设计方案中,除装药量和爆心距外,其他参数(如布孔方式、钻孔深度、装药参数等)基本一致。将试验方案的振速信号作为基础信号,按比例放大后,可近似模拟分析设计爆破方案下的爆破振动对尾矿坝的影响。测点1#位于模型y向最小处,是数值模拟时爆破载荷的输入位置。因此,选取试验I中的测点1#的振速信号进行比例放大处理。
根据萨道夫斯基公式计算爆破设计方案下,尾矿坝测点1#峰值振速为0.261cm/s;试验I方案下测点1#的峰值振速为0.041cm/s;放大倍数为二者比值。经计算,放大了6.37倍。
将Midas GTS非线性动力分析中输入的载荷作为加速度信号,模拟前需要对监测得到的速度信号进行微分转化。转化后,放大系数并未变化,但容易增加噪声信号。因此,需要对转化的加速度信号进行滤波和基线校正处理。处理后的信号可作为爆破振动载荷输入到模型中进行计算分析。
为分析安全允许质点速度与尾矿坝坝体稳定安全系数间的关系,将输入载荷最大振速逐步增加并进行稳定性计算,选取2种典型的工况进行详细分析。其中,设计爆破方案下的爆破载荷作为工况a,初期坝坝脚振速阈值达到8cm/s下对应的爆破载荷为工况b。
工况a中,测点1#计算的峰值振速为0.261cm/s,经上述转化后输入的爆破载荷的最大加速度为0.240cm/S2,放大6.37倍。工况b中,测点1#计算的峰值振速为8.000cm/s,此载荷最大加速度为7.220cm/S2,放大195.12倍。
3模拟计算及结果分析
各工况稳定计算结果如图5所示。
计算结果表明,在工况a下,坝体稳定安全系数Fs为1.33 >1.10;在工况b下,坝体稳定安全系数Fs为1.10 =1.10,均满足GB 39496-2020《尾矿库安全规程》中关于四等库特殊运行工况下的抗滑稳定要求。
设计爆破方案条件下,贯通坝体的塑性区域位于堆积坝713.0m标高以上,此处为受爆破振动影响最大的区域。建议加强此区域的坝体检测,确保在后续爆破削坡工程实施前此区域无变形、裂缝、滑坡和渗漏等现象,浸润线埋深、外坡坡比等满足设计要求。
将各振速阈值对应下的爆破载荷输入到模型进行稳定性计算,可得到尾矿坝坝体稳定安全系数与安全允许质点速度阈值的关系曲线,如图6所示。
分析图6可知,在速度阈值为0时(即无爆破时),尾矿坝稳定性安全系数为1.33。随着输入载荷速度阈值强度的增加,速度阈值在3cm/s时,稳定性安全系数由1.33降低至1.30,降低了2%,整体变化不大。速度阈值在8cm/s时,稳定性安全系数由1.33降低至1.10,降低了17%。此时,稳定安全系数达到了规范要求的坝坡抗滑稳定的最小安全系数。
在爆速阈值小于3cm/s时,坝体安全系数变化不大;大于3cm/s后,尾矿坝体稳定安全系数骤降。此速度为安全系数变化的分界,将本尾矿坝安全允许质点速度取3cm/s。
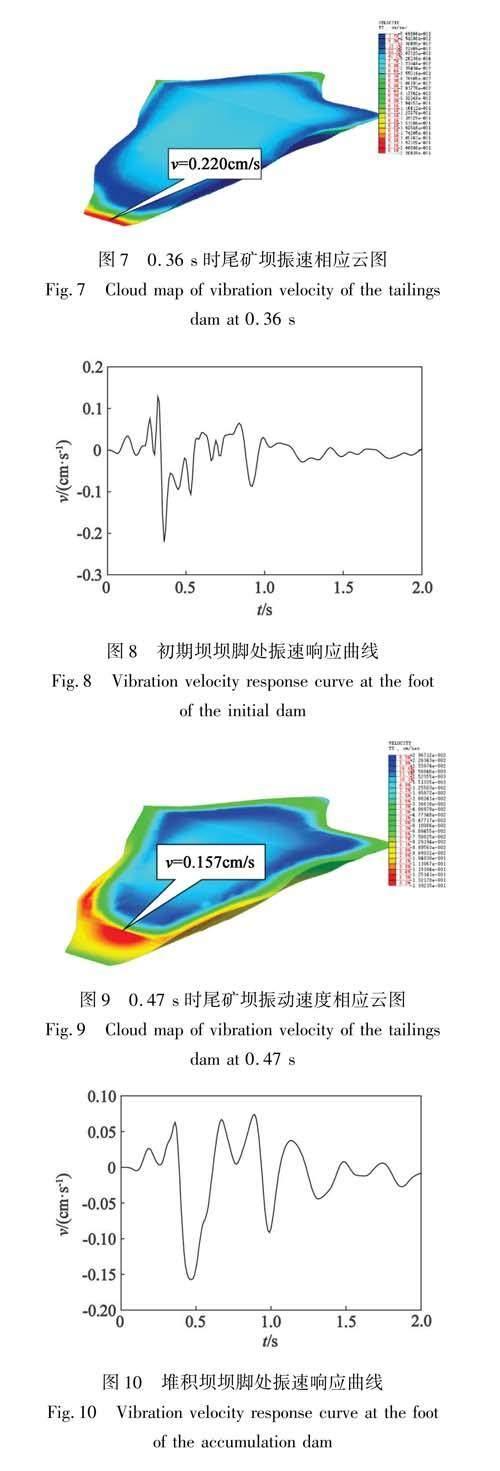
在设计爆破方案下,初期坝峰值振速出现在0.36s,节点位于初期坝坝脚处,最大振速为0.220cm/s,满足安全允许质点速度要求,如图7所示。此节点处的振速响应曲线如图8所示。
堆积坝峰值振速出现在0.47s,节点位于初期坝坝顶堆积坝坝脚处,峰值振速为0.157cm/s,如图9所示。此节点处的振速响应曲线如图10所示。
在爆破削坡工程实施过程中,对前述测点的振速进行了监测,实际监测数据和数值模拟对比结果如表4所示。
表4中,测点2#~5#的数值模拟结果误差较小,实测值和模拟结果均小于本尾矿坝的安全允许质点速度3cm/s,说明本次爆破对尾矿坝稳定性的影响较小。
4结论
1)根据试验方案监测的振动波形频率表明:本次露天深孔爆破振动主頻在0~50Hz之间,模拟与《爆破安全规程》露天深孔爆破的振动频率范围基本一致。
2)采用萨道夫斯基公式分析试验监测数据,可以得到公式中的参数K和a,将试验得到的振动信号放大作为输入源,可分析相应爆破参数下的尾矿坝稳定性和坝体的振动响应,能够预测爆破设计方案条件下尾矿坝的最大振速。
3)分析尾矿坝在不同速度阈值下对应的稳定性,并通过尾矿坝稳定性的变化趋势,可确定尾矿坝安全允许质点速度。在坝体峰值振速小于速度阈值时,可保证尾矿坝稳定性不受爆破振动影响。

