基于时频域特征和朴素贝叶斯的滚动轴承故障诊断方法研究

温翔采 张清华 胡勤 刘迪洋

摘 要：【目的】为了解决滚动轴承故障特征提取困难、诊断性能偏低的问题，提出了一种基于时频域特征和朴素贝叶斯的故障诊断方法。【方法】首先，通过局部均值分解方法对原始振动信号进行处理，获得多个乘积函数分量。其次，基于原始振动信号和各个乘积函数分量，提取时频域特征，并采用主成分分析实现特征降维，获得低维敏感特征。最后，依据低维敏感特征集，结合朴素贝叶斯模型，实现对江南大学—机械工程学院滚动轴承数据集的分析。【结果】实验结果表明，该方法相较于传统朴素贝叶斯准确率高39.49%，相较于主成分分析准确率高5.94%，由此得出该方法对滚动轴承故障的诊断表现较好。【结论】对于传统的单一的故障诊断模型，基于时频域特征和朴素贝叶斯的故障诊断模型具有更高的准确率，解决了滚动轴承故障特征提取困难、诊断性能偏低的问题。

关键词：滚动轴承；时频域特征；局部均值分解；主成分分析；朴素贝叶斯

中图分类号：TP181     文献标志码：A     文章编号：1003-5168（2024）07-0018-07

DOI：10.19968/j.cnki.hnkj.1003-5168.2024.07.004

Research on Fault Diagnosis Method for Rolling Bearings Based on Time Frequency Domain Features and Naive Bayes

WEN Xiangcai1 ZHANG Qinghua2 HU Qin2 LIU Diyang1

（1. Jilin Institute of Chemical Technology， Jilin 132000， China;

2. Guangdong University of Petrochemical Technology， Maoming 525000， China）

Abstract： [Purposes] In order to solve the problems of difficult feature extraction and low diagnostic performance of rolling bearings， a fault diagnosis method based on time-frequency domain features and naive Bayes is proposed. [Methods] This method first processes the original vibration signal through local mean decomposition to obtain multiple product function （PF） components. Secondly， based on the original vibration signal and various PF components， time-frequency domain features are extracted， and principal component analysis is used to achieve feature dimension reduction， obtaining low dimensional sensitive features. Finally， based on the low dimensional sensitive feature set and combined with the naive Bayesian model， the analysis of the rolling bearing dataset from Jiangnan University School of Mechanical Engineering is achieved. [Findings] The experimental results show that the accuracy of this method is 39.49% higher than that of traditional naive Bayes， and 5.94% higher than that of principal component analysis. Therefore， it can be concluded that this method performs well in diagnosing rolling bearing faults. [Conclusions] Compared to traditional single fault diagnosis models， fault diagnosis models based on time-frequency domain features and naive Bayes have higher accuracy and solve the problems of difficult feature extraction and low diagnostic performance in rolling bearing faults.

Keywords： rolling bearings; time-frequency domain features; local mean decomposition; principal component analysis; naive bayes

0 引言

石化產业作为国民经济的支柱产业，在提高生活水平、促进经济增长、保障国家安全等方面具有重要意义［1］。在石化机组中，滚动轴承作为重要的组成部分，也是最容易发生故障的零部件之一［2］。轴承故障将影响旋转机械的正常工作，甚至使石化机组停止运行，因此研究石化机组轴承的故障预测、故障诊断具有重要意义［3］。

目前有关贝叶斯的相关理论在故障诊断领域已经得到了大量应用。刘兆伦等［4］提出了一种增量式贝叶斯算法对篦冷机进行故障诊断，在加入新数据时，对其结构是否需要更新做出判断，并对网络结构参数进行动态更新；梁博阳等［5］提出了一种基于参数残差驱动贝叶斯网络的冷水机组故障诊断的方法，构建特征参数基准值模型，使用基准值和实际值之间的参数残差训练贝叶斯网络模型；Yu等［6］提出了一种基于动态贝叶斯网络故障诊断方法，该方法考虑了传感器和系统设备退化对诊断结果的影响，避免了静态诊断网络中的过诊断问题；Yasenjiang［7］提出了一种隐马尔可夫模型和贝叶斯网络混合模型，该方法引入专家知识构造贝叶斯网络以准确诊断故障根源变量，通过序贯和并行学习对期望最大算法进行改进。

为了克服滚动轴承故障特征提取困难、诊断性能偏低的问题，本研究提出了基于时频域特征和朴素贝叶斯的故障诊断方法。具体而言，首先通过局部均值分解方法对原始振动信号进行处理，获得多个乘积函数（Product function，PF）分量。其次，基于原始振动信号和各个乘积函数分量，提取时频域特征，并采用主成分分析实现特征降维，获得低维敏感特征。最后，依据低维敏感特征集，结合朴素贝叶斯，进行训练和故障诊断。

1 基本理论

1.1 局部均值分解

SMITH J S于2005年提出了一种自适应的信号分解方法—局部均值分解（Local Mean Decomposition，LMD）［8］。该方法自适应地将一个复杂的、非平稳的信号分解为若干个瞬时频率且具有物理意义的乘积函数之和，其中每一个PF分量可以由一个包络信号和一个纯调频信号直接求出。相较于经验模态分解方法，LMD方法对端点效应具有一定的抑制性，同时能够解决包络不足和包络过度的问题［9］。对于任意信号[x（t）]，LMD主要步骤如下［10］ 。

①找出[x（t）]局部范围内的全部极值点[qi]，局部平均值[mi]，见式（1）。局部包络值[ai]，见式（2）。

[mi=qi+qi+12] （1）

[ai=qi?qi+12] （2）

②将①中得到的[mi]和[ai]连接并做平滑处理，得到局部平均值函数[m11（t）]和局部包络值函数[a11（t）]。之后将[m11（t）]从原始信号中分离，得到[?11（t）]，见式（3）。用[?11（t）]与[a11（t）]做比值，得到调频信号[s11（t）]，见式（4）。

[?11t=xt?m11t] （3）

[s11t=?11ta11t] （4）

③重复步骤①，求得[s11（t）]的局部包络值函数[a12（t）]，若[a12t=1]，则[s11（t）]为纯调频信号，计算结束；若[a12t≠1]，则重复步骤①，见式（5）。

[?11（t）=x（t）?m11（t）?12（t）=s11（t）?m12（t）??1n（t）=s1n?1（t）?m1n（t）] （5）

其中[s1n（t）]的具体表达形式，见式（6）。

[s11（t）=?11（t）/a11（t）s12（t）=?12（t）/a12（t）?s1n（t）=?1n（t）/a1n（t）] （6）

理论上，迭代终止条件为[limn→∞ a1n（t）=1]，在实际情况中，得不到等于1的结果，只能无限接近1，所以当[a1（n+1）（t）≈1]即可结束迭代过程。

④当迭代满足终止条件时，可以计算得到瞬时幅值函数和乘积函数分量，见式（7）。

[a1t=a11ta12t…a1nt=q=1n a1zt]

[PF1t=a1ts1zt] （7）

⑤从原始信号[x（t）]中提取出[PF1（t）]，得到新的信号[u1（t）]，将[u1（t）]视为新的原始信号，重复上述过程k次，直到[uk（t）]为满足单调函数为止，见式（8）。

[u1（t）=x（t）?PF1（t）u2（t）=u1（t）?PF2（t）?uk（t）=uk?1（t）?PFk（t）] （8）

这时，原始信号[x（t）]便被分解为若干个PF分量和一个残差分量[uk（t）]，见式（9）。

[xt=p=1k PFpt+ukt] （9）

1.2 时频域特征提取

为更加充分地获取故障信息，本研究采用时频域特征提取故障特征。根据Lei等［11］的研究，提取了11个时域特征量和10个频域特征量。各个特征的具体计算公式见表1。

1.3 主成分分析

主成分分析（Principal Component Analysis，PCA）是一種使用广泛的数据降维算法，能够在原有N维特征的基础上重新构造出全新正交的K维特征，即主成分［12－13］。PCA算法的主要步骤如下。

①数据预处理：中心化，计算数据的协方差矩阵 [1mXXT]。

②其中协方差描述两个数据的相关性，接近1为正相关，接近-1为负相关，接近0为不相关。两个数据的协方差计算公式，见式（10）。

[covX，Y=i=1n Xi?XYi?Yn?1] （10）

③对协方差矩阵做特征值分解。

④选出最大的K个特征值对应的K个特征向量。

⑤将原始数据投影到选取的特征向量上。

⑥输出投影后的数据集。

1.4 朴素贝叶斯

贝叶斯定理描述2个条件概率间的关系，通常事件A在事件B发生条件下的概率，与事件B在事件A发生条件下的概率不同，但二者具有确定关系［14］。贝叶斯公式便是基于条件概率，通过[PB|A]来求[PA|B]，见式（11）、式（12）。

[PA|B=PABPB] （11）

[PA|B=PB|A×PAPB] （12）

条件概率是所有属性上的联合概率，难以从有限的训练样本直接估计而得。为避开这个障碍，朴素贝叶斯（Naive Bayes，NB）采用了“属性条件独立性假设”。对已知类别，假设所有属性相互独立，即假设每个属性独立地对分类结果发生影响［15］。可以说，朴素贝叶斯网络是一种简化的贝叶斯网络形式。在朴素贝叶斯中，假设给定类别的情况下，特征之间是相互独立的。这个假设使得朴素贝叶斯模型的参数估计和推断更加简单和高效。

假定在朴素贝叶斯网络中，各属性节点之间相互独立，仅与类节点C有关联。构建贝叶斯网络模型的复杂性因网络层数的减少，它的构建难度得以指数级降低。基于属性条件独立性假设［16］，见式（13）。

[Pc|x=PcPx|cPx=PcPxi=1d Pxi|c   13]

式中：[d]为属性数目；[xi]为[x]在第[i]个属性上的取值。

由于對所有类别来说[P（x）]相同，只需求得并筛选出概率值最大的即可，因此基于贝叶斯判定准，见式（14）。

[?nbx=argmaxc∈Y Pci=1d Pxi|c] （14）

虽然朴素贝叶斯网络中的“属性条件独立性假设”通常较难满足，但朴素贝叶斯网络仍然具有一定的适用性［17］。Pedro等［18］通过实验证明，“属性条件独立性假设”不成立时，朴素贝叶斯网络依然可能得到比较满意的分类结果，是因为朴素贝叶斯网络所需训练参数相对于贝叶斯网络较少，可以有效地避免过拟合情况的发生。

2 基于时频域特征和朴素贝叶斯的故障诊断模型构建

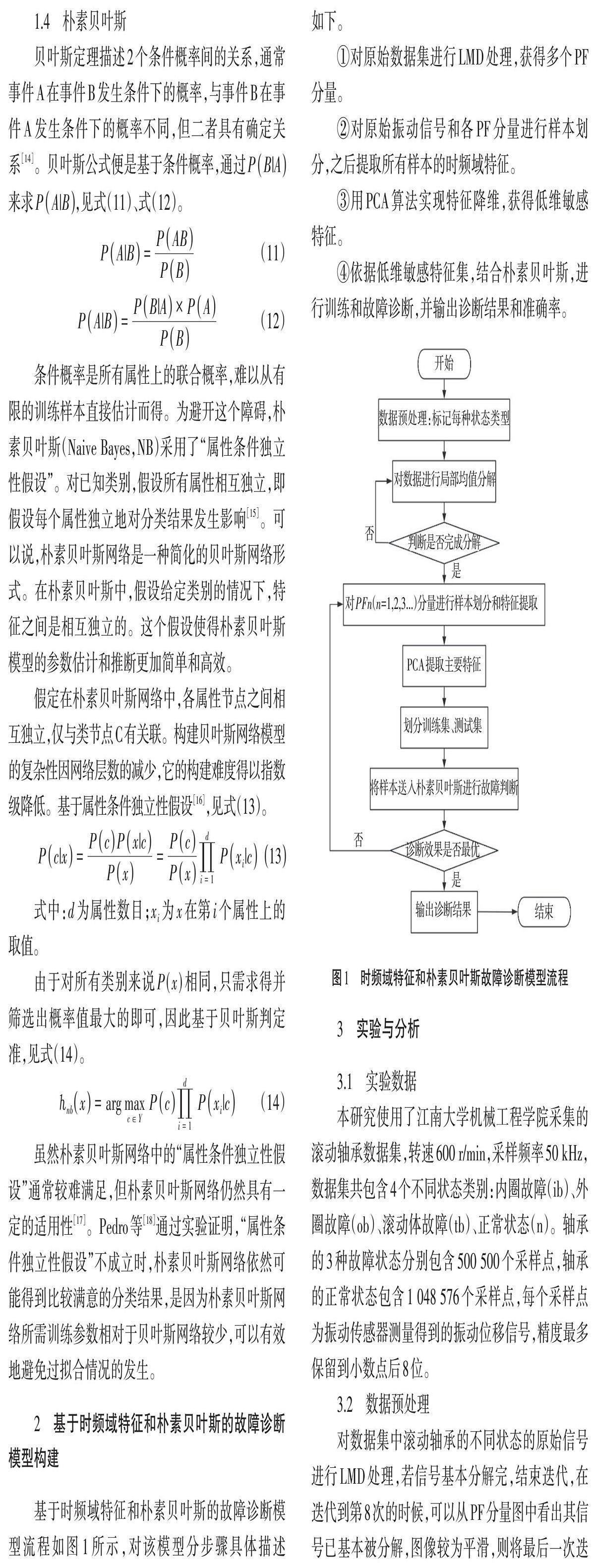
基于时频域特征和朴素贝叶斯的故障诊断模型流程如图1所示，对该模型分步骤具体描述如下。

①对原始数据集进行LMD处理，获得多个PF分量。

②对原始振动信号和各PF分量进行样本划分，之后提取所有样本的时频域特征。

③用PCA算法实现特征降维，获得低维敏感特征。

④依据低维敏感特征集，结合朴素贝叶斯，进行训练和故障诊断，并输出诊断结果和准确率。

3 实验与分析

3.1 实验数据

本研究使用了江南大学机械工程学院采集的滚动轴承数据集，转速600 r/min，采样频率50 kHz，数据集共包含4个不同状态类别：内圈故障（ib）、外圈故障（ob）、滚动体故障（tb）、正常状态（n）。轴承的3种故障状态分别包含500 500个采样点，轴承的正常状态包含1 048 576个采样点，每个采样点为振动传感器测量得到的振动位移信号，精度最多保留到小数点后8位。

3.2 数据预处理

对数据集中滚动轴承的不同状态的原始信号进行LMD处理，若信号基本分解完，结束迭代，在迭代到第8次的时候，可以从PF分量图中看出其信号已基本被分解，图像较为平滑，则将最后一次迭代的得到的残差结果命名为PF0，放在原始信号的下方，其他PF1至PF7的分量依次排在下方。内圈故障（ib）前10 000个采样点的分解波形如图2所示。

3.3 特征处理与PF分量选择

首先对数据集进行样本划分，选取连续500个采样点作为一个样本，则3种故障状态的每个PF分量可以划分为1 001个样本，正常状态的每个PF分量可以划分为2 098个样本。根据21种故障特征进行特征提取。

PF分量得到的故障特征集中的数据存在冗余和不相关信息，容易对诊断模型的训练和诊断产生影响，因此使用PCA方法对故障特征集进行降维，根据降维后的各主成分的方差值占总方差值的比例，即方差贡献率，选取前10个主成分作为最终的故障特征，并对降维后的故障特征集做标准化处理。

每个轴承运行状态各拥有7个PF分量，越接近原始信号的分量保留的信号特征则越多，同时保留了越多冗余和不相关信息。如果将所有分量都使用模型进行训练，则失去了LMD对数据进行处理的意义，因此，需要选出一个既保留了大部分原始信号特征，且又剔除了更多杂乱特征的PF分量。经过对每个PF分量分别计算后得出，PF6分量相较于其他分量更符合要求，如图3、表2所示。

3.4 不同方法对比实验

通过实验与分析，得出PF6分量代表PF分量中的最优。接下来围绕PF6分量展开分析。

首先是测试集与训练集的划分：将所有样本划分为训练集65%，测试集35%。其中ib、ob、tb分别有1 001个样本，n有2 098个样本，共有5 101个样本，按照划分比例，训练集包含3 316个样本，测试集包含1 785个样本。

实验主体主要分为3组对照实验，包括：传统朴素贝叶斯进行诊断、对原始特征进行PCA处理后使用朴素贝叶斯进行诊断、本研究提出的基于时频域特征和朴素贝叶斯的故障诊断模型。不同组对照实验的准确率，见表3；每组中不同故障类型各自的准确率，见表4。

相较于其他2组对照实验，基于时频域特征和朴素贝叶斯的故障诊断模型在故障诊断准确率上均高于其他方法。该模型对比传统的朴素贝叶斯准确率高39.49%，对比只使用PCA算法处理数据的方法准确率高5.94%。

4 结论

为改善对滚动轴承故障的诊断效果，本研究提出了一种基于时频域特征和朴素贝叶斯的故障诊断方法。该方法结合了时频域特征、局部均值分解、主成分分析、朴素贝叶斯等因素，通过对照实验对该方法的有效性进行了验证，得到以下结论。

该方法与直接使用朴素贝叶斯进行诊断相比准确率高39.49%，说明该方法既能最大程度地消除冗余信号和噪声信号，又能最大程度地保留原始信号的特征，保证其对原始信号故障特征地充分提取；该方法与不使用LMD方法来处理原始信号，只使用PCA进行特征降维相比准确率高5.94%，说明LMD方法对于处理复杂的非平稳的信号具有不错的效果。相较于传统的单一的故障诊断模型，基于时频域特征和朴素贝叶斯的故障诊断模型具有更高的准确率，该模型解决了滚动轴承故障特征提取困难、诊断性能偏低的问题，避免了由模型诊断错误率高、诊断不及时造成的人员和财产损失。

参考文献：

［1］刘鸣慧，熊建斌，蘇乃权，等.基于深度学习的石化机组轴承故障诊断综述［J］.机床与液压，2023，51（6）：171-180.

［2］EREN L， INCE T，KIRANYAZ S.A generic intelligent bearing fault diagnosis system using compact adaptive 1d cnn classifier［J］.J Signal Process Syst，2019，91（2）：179-189.

［3］ LEI Y G，LIN J，ZUO M J，et al.Condition monitoring and fault diagnosis of planetary gearboxes： a review［J］.Measurement，2014，48：292-305.

［4］刘兆伦，张春兰，武尤，等.一种增量式贝叶斯算法及篦冷机故障诊断［J］.中国机械工程，2019，30（10）：1163-1171.

［5］梁博阳，郭景景，王占伟，等.基于参数残差驱动贝叶斯网络的冷水机组故障诊断［J］.过程工程学报，2023，23（4）：627-636.

［6］YU H，YU J X，WANG C，et al．A fault diagnosis method for the hipps of fpso unit based on dynamic bayesian network［J］.Proceedings of the Institution of Mechanical Engineers，2023，237（4）：752-764.

［7］YASENJIANG J，XU C X，ZHANG S P，et al.Fault diagnosis and prediction of continuous industrial processes based on hidden markov model-bayesian network hybrid model［J］.International Journal of Chemical Engineering，2022.

［8］SMITH J S.The local mean decomposition and its application to eeg perception data［J］.J R Soc Interface，2005，2（5）：443-454.

［9］徐石，栾孝驰，李彦徵，等.基于LMD与AO-PNN的中介轴承故障诊断方法［J］.航空发动机，2024，50（2）：114-120

［10］赵光昌.EMD及其改进和无量纲分析相结合的轴承故障定位研究［D］.太原：太原理工大学，2015.

［11］LEI Y G， HE Z J， ZI Y Y，et al.Fault diagnosis of rotating machinery based on multiple anfis combination with gas［J］.Mech Syst Signal Process，2006，21（5）：2280-2294.

［12］张燕飞，李赟豪，王东峰，等.基于多源信息融合的滚动轴承故障监测方法［J］.轴承，2022（12）：59-65.

［13］KOUADRI A，HAJJI M，HARKAT M F，et al.Hidden markov model based principal component analysis for intelligent fault diagnosis of wind energy converter systems［J］.Renewable Energy，2020，150：598-606.

［14］刘超.基于贝叶斯定理的船舶交通事故环境因素分析［J］.山东交通学院学报，2023，31（3）：162-166.

［15］周志华.机器学习［M］.北京：清华大学出版社，2016.

［16］刘锦松.基于朴素贝叶斯网络和D-S证据理论的分布式电网故障诊断［J］.海峡科技与产业，2021，34（5）：88-93.

［17］程晓宜.基于多维特征和组合分类器的水电机组故障诊断方法研究［D］.武汉：武汉大学，2019.

［18］PEDRO D，MICHAEL P.On the optimality of the simple bayesian classifier under zero-one loss［J］.Mach Learn，1997，29（2-3）：103-130.

收稿日期：2024-01-17

作者简介：温翔采（1997—），男，硕士生，研究方向：故障诊断。

通信作者：张清华（1965—），男，博士，教授，研究方向：人工智能、状态监测与故障诊断。