半圆梁框架变张力缠绕工艺计算方法

李博取

摘 要：区别于传统半圆梁缠绕预紧的变张力计算方法的钢丝预应力相同（A型）和工作应力简化为一次变化的钢丝工作总应力相同（B型），本文提出一种利用计算机计算钢丝工作总应力相同的变张力计算方法D型。特点在于：将积分求解函数变为散点逆推的方法;对一些传统计算公式进行便于计算机计算的调整;增加保护层缠绕影响的计算概念;等张力台阶拟合变张力曲线计算时增加一个拟合数以快速得到工艺输出结果。

关键词：半圆梁框架;钢丝缠绕工艺;变张力缠绕;陶瓷压机

1前 言

缠绕框架对于陶瓷压机来说非常合适，框架刚性要求不高，工作台面不大，工作行程小，因此目前国内外的传统陶瓷压机普遍采用缠绕式预紧框架。而对于缠绕框架来说，最重要的莫过于钢丝缠绕工艺。随着计算机的发展，目前框架设计已经由过去的详细计算变成了如今的草算加有限元分析，但是钢丝缠绕计算仍然需要进行详细计算。目前借用计算机进行计算时，传统算法如文献[1]中一些公式简化已经不再需要，B型需要反复修改参数计算的缺点也不再是问题，而将其中求解函数关系式的方法变为散点逆推求解则能节省大量的中间变量和计算公式，且不再需要将工作应力简化为直线分布。

本文对于具体公式不进行推导和详细解释，大部分公式来自于文献[1-2]及其推导，即本文同样采用了经典的一般理想半圆梁框架静力平衡和变形协调联立求解的方法。作为与A型和B型做区分，本文将该算法定义为D型。另外本算法增加了保护层对缠绕工艺的影响的计算概念，以及通过增加一个拟合数来自动生成台阶应力的方法，本文不对公式进行推导解释。

按照本文方法创建计算机表格（如WPS），开发新机型时可以非常快捷的得到缠绕工艺结果，且表格数据非常便于建立图表分析，本文不对这一部分进行叙述，由读者自行尝试。

注：本司缠绕工艺与文献[3]中转盘式缠绕技术相同。

主要名词解释：1）钢丝预应力：缠绕完成后，直边位置的预紧钢丝所受到的拉应力;2）缠绕初应力：钢丝缠绕时正在缠绕的钢丝因工艺配重所受到拉应力;3）钢丝工作应力：当工作负载为满载荷时钢丝增加的拉应力;4）钢丝工作总应力：当工作负载为满载荷时钢丝所受到拉应力;5）立柱预紧力：立柱所受到的压力，作为框架的预紧力。

2 案例计算

计算前提以及假设：1）直线段钢丝比曲线段钢丝更危险，因此按直线段进行设计计算;2）忽略半圆梁变形和立柱弯曲变形以及立柱与半圆梁的楔形间隙;3）忽略进行缠绕时已缠绕曲边钢丝变形;4）忽略半圆梁与立柱的楔形间隙;5）忽略同一层钢丝的应力不均匀分布。

钢丝缠绕工艺的计算步骤：1）求解各层钢丝的工作应力;2）由工作应力和许用应力求出各层钢丝预应力;3）求出各层钢丝的缠绕初应力;4）将该初应力实现为工艺配重;5）工艺实现验证。

下面以一个算例展开，注意下列表格数据均为本案例最优迭代结果，忽略迭代过程。

现有一1500吨（P=15MN）半圆梁缠绕框架陶瓷压机，立柱数i=2，期望预紧系数η0=1.05，保护层N=3层（工艺确定）;单边立柱截面积Fc=120400mm2;半圆梁缠绕层内径R1=1030mm;直边长度L=1846mm;钢丝槽宽BL=340mm。

立柱材料选用ZG270～500，弹性模量Ec=180.13Gpa[4]。重力加速度取广州g=9.79m/s2。

钢丝选用65Mn冷轧扁钢丝[5]，弹性模量Ew=195GPa;钢丝高宽：h×b=1.5mm×5mm;钢丝截面积f= 5×1.5-0.18×1.52 = 7.095mm2;钢丝抗拉强度σb=1620MPa;[σ]=810MPa钢丝许用应力。

缠绕工艺配重块重量：基础块m1=150kg，大配重块m2=25kg，小配重块m3=5kg。为方便后续计算，m1和m2均为m3的整数倍，配重重量以工艺配置为准，一般只需要分为三种重量即可，其中小配重块重量越小，等张力拟合波动越小。

2.1确定缠绕层数

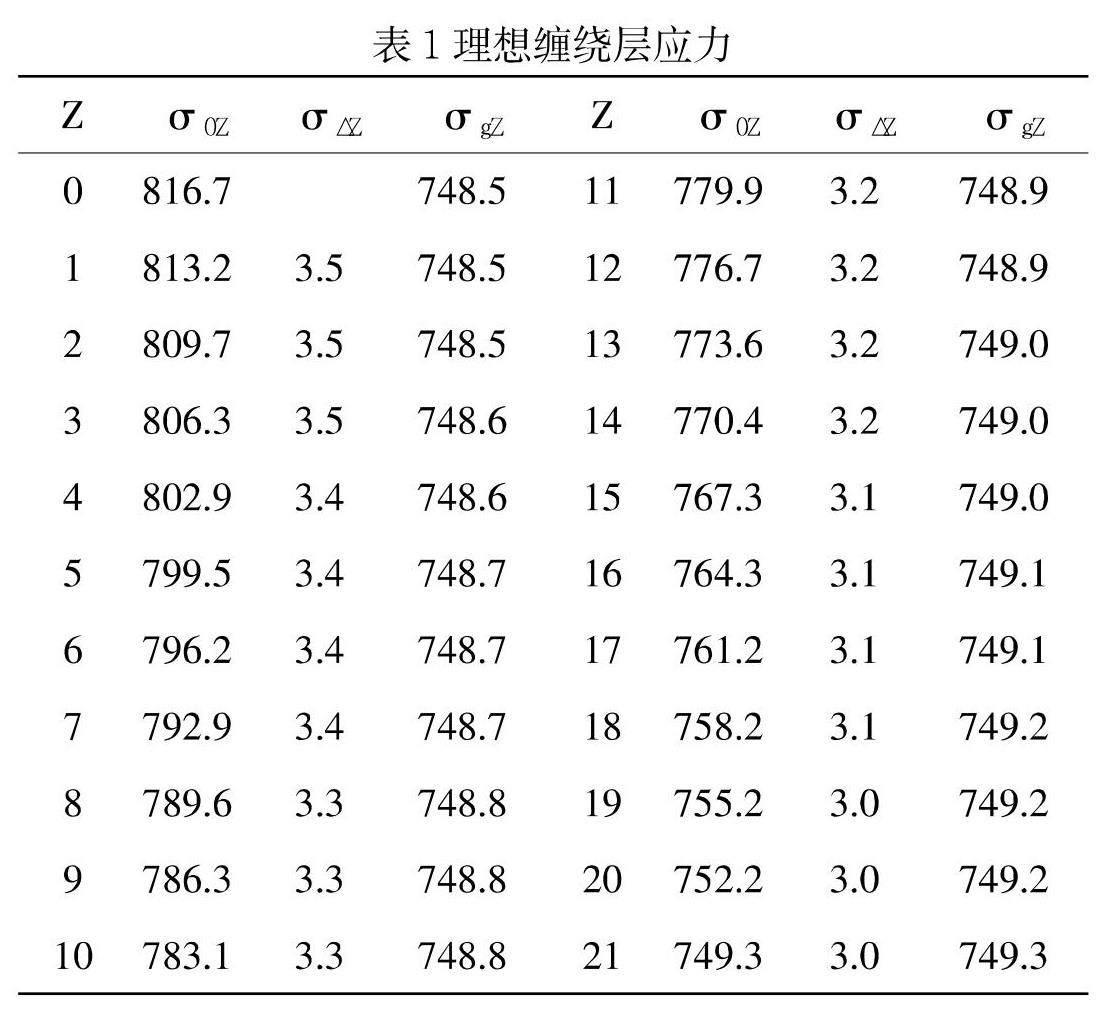
2.2求解理想缠绕初应力

第Z层缠绕层预紧应力（不计算保护层影响）：

2.3求解等张力台阶配重

（1）缠绕层工艺计算表格。

设每个等张力台阶层数为T，拟合数H（表格中数据取T=3，H=1.5），第n个台阶的缠绕层从到，从表1中获取数值带入下列公式求各台阶的理想缠绕初应力：

σ0n理=σ0 T  （ n-1）-（σ0 T  （n-1）-σ0T  n）/H;

（2）保護层工艺计算表格

保护层配重手动输入，基础块数量为1不变，大配重块数量A，小配重块数量B，保护层配重：

Mn=m1+Am2+Bm3;

实际台阶应力：σ0 i=Mi g/2f;

影响应力引用式2-2;

第Z层钢丝产生的立柱预紧力：

本案例通过给第一层保护层19个A以补偿层数选择21层后所缺少的预紧力，以保证达到理想预紧力状态。

结合上述公式制作得到表3。

保护层影响应力：

σ△保=σ△22+σ△23+σ△24=2.53MPa;

保护层产生立柱预紧力：Pc保=0.28MN;

2.4求解工艺缠绕应力

钢丝层缠绕初应力σ0Z引用表2数据（例如OFFSET函数）;影响应力σ△Z同式2-2;第Z层钢丝产生的立柱预紧力Pc i同式2-3;

工作总应力：σ总Z=σg Z+（[σ]-σg Z）-σ△保。结合上述公式制作得到表4。

总预紧力Pc总=i（Pc+Pc保）=15.74MN;

拟合误差△拟合=Pc总-Pη0=- 0.05%;

总应力△极差=MAX（σ总Z）-MIN（σ总Z）=8.67MPa。

2.5确定变量

（1）台阶层数T：以△极差＜10MPa，作为缠绕台阶层数T（正整数）的判定标准，该值越大，缠绕工艺越方便无需频繁更换配重，但应力极差会增加。

（2）保護层配重：以△拟合作为保护层配重的选择标准，默认三层皆为基础块配重。因有19个A焊在一起的配重块，所以本案例选择A=19来补偿框架预紧力。保护层配重尽量只加在第一层上，另外两层以基础块配重缠绕即可。

（3）拟合数H：以△极差尽量小和△拟合尽量接近0作为拟合数H的判定标准。

2.6输出结果

将表2的缠绕层配重数量以及表3的保护层配重数量交给工艺执行，计算完毕。

3 结语

虽然此类计算方法（理想框架的力平衡加变形协调）误差不小，但是必然能够保证钢丝安全。

首先因计算平均工作应力时忽略了曲边钢丝形变，造成实际钢丝工作应力总小于计算工作应力;其次因立柱弯曲，造成框架立柱缠绕槽的形变小于理想形变，造成实际钢丝预应力小于计算预应力;此两误差影响很大，因此可以认为实际预紧力总是大于计算预紧力（降低计算预紧系数的根本原因），实际钢丝应力总是小于计算应力，因此除了会造成少量浪费以外，此算法十分安全有效。

虽然随着有限元分析的出现，钢丝缠绕计算已经可以从有限元分析结果反向推导钢丝缠绕初应力，但是该方法过于复杂且没有经过长期的使用验证，实用性不高。因此本文所述算法目前仍然因其简便性和可靠性有着非常广泛的应用。

参考文献

[1]颜永年;俞新陆.机械设计中的预应力结构[M].1989：114-128.

[2]韩文;肖任贤;许志华.缠绕型全自动液压压砖机机架钢丝预紧力的设计[J].锻压装备与制造技术，2004，（01）：17-19.

[3]邓晨曦;吴任东;颜永年;张磊;彭俊斌.大型承载框架钢丝预应力缠绕技术研究[J].新技术新工艺，2008，（02）：52-54+3.

[4]张庆玲;张荣强;金淼.应变控制方式下ZG270-500材料特性试验研究[J].燕山大学学报，2019，（05）：449-454.

[5]YB/T 4295-2012.承压机械设备缠绕用扁钢丝[S].中华人民共和国工业和信息化部.2013-03-01实施.