降雨时空不确定性对小流域洪峰模拟的影响评估

王雪梅　郭良　翟晓燕

摘 要：山丘区小流域洪峰模拟结果与降雨时空分布密切相关。以河南省荥阳市王宗店流域“７·２０”山洪灾害为例，构建了１５ 种时空分布的１０ ｍｉｎ 尺度降雨情景，综合采用中国山洪水文模型和方差分析理论评估降雨时空情景变化对洪峰模拟的影响。结果表明：中国山洪水文模型可以较好地模拟“７·２０” 暴雨洪水过程。不同时间情景下１０ ｍｉｎ 降雨量均匀分布模拟得到的洪峰流量较小、峰现时间较晚；非均匀分布时最大１０ ｍｉｎ 降雨量发生时间越晚，模拟得到的洪峰流量越大、峰现时间越晚。空间情景变化主要影响洪峰流量模拟，采用泰森多边形法模拟得到的洪峰流量最大。时间情景变化是洪峰流量和峰现时间模拟结果不确定性的最主要来源，空间情景变化和时空情景耦合变化仅影响洪峰流量模拟。

关键词：暴雨山洪模拟；降雨时空不确定性；中国山洪水文模型；方差分析；王宗店流域

中图分类号：Ｐ３３３．２ 文献标志码：Ａ ｄｏｉ：１０．３９６９／ ｊ．ｉｓｓｎ．１０００－１３７９．２０２４．０４．００８

引用格式：王雪梅，郭良，翟晓燕．降雨时空不确定性对小流域洪峰模拟的影响评估［Ｊ］．人民黄河，２０２４，４６（４）：４９－５４．

水文模型利用概化的数学物理方程描述流域雨洪响应过程，实现对暴雨洪水的模拟和预警预报［ １］ 。受模型输入、模型结构和模型参数等因素不确定性的影响，流域径流模拟结果的不确定性客观存在且不可忽视［２］ 。山丘区暴雨洪水时空异质性强、产汇流过程非线性特征显著［３］ ，暴雨山洪模拟的难度大、不确定性强［４］ 。厘清导致山洪模拟不确定性的关键要素，控制场次模拟结果的变化区间，是提高山洪灾害预警预报可靠度与准确性的重要途径。

模型输入（降雨、流量等）的不确定性是水文模拟结果不确定性的主要原因［５］ 。国内外已有不少学者针对降雨输入的不确定性对洪水模拟效果的影响展开研究。陈华等［６］ 基于新安江模型和ＨＢＶ 模型研究了雨量站密度和空间分布对湘江流域径流模拟的影响，发现增加雨量站密度、优化站点空间分布可以提升场次径流过程模拟精度。Ｓｉｌｖｅｓｔｒｏ 等［７］ 基于概率性洪水预报框架评估了降雨时空尺度对意大利Ｂｉｓａｇｎｏ Ｃｒｅｅｋ流域洪水模拟的影响，提出了研究区次洪模拟的最佳时空尺度配置方案。Ｌｉｕ 等［８］ 构建了２０ 种流域降雨输入方案以探究时空尺度对半干旱地区洪水模拟的影响，指出降雨时间尺度对次洪模拟的影响显著。李大洋等［９］ 评估了ＭＩＫＥ ＳＨＥ 在淮河黄泥庄流域水文模拟的尺度适应性，发现洪水模拟结果对网格尺寸与时间步长的敏感性主要体现在洪峰和洪量上。已有研究多关注不同降雨时空特征的次洪模拟结果变化规律，各种不确定性对洪水模拟结果变化的贡献有待进一步量化。

相较于大流域雨洪模拟，山丘区小流域更侧重于对洪水洪峰的模拟预报［１０］ 。本文以２０２１ 年７ 月２０日发生于河南省荥阳市王宗店流域的山洪灾害（“７·２０”山洪灾害）为例，基于累积降雨量—历时之间的回归关系和设计条件下的雨峰特性对实测小时降雨量进行时间上的降尺度插值，基于测站降雨量采用泰森多边形法、反距离权重法和等雨量线法进行空间上的流域降雨量插值，综合利用中国山洪水文模型和方差分析理论定量评估降雨时空分布變化对山丘区洪水洪峰模拟的影响，以期为山丘区小流域洪水模拟的不确定性评估提供指导与帮助。

１ 研究区概况及数据源

王宗店流域位于河南省北部山丘区（ 东经１１３°１７′—１１３°２２′ ，北纬３４°３６′ —３４°３９′ ），见图１，集水面积２１．７ ｋｍ２。研究区属亚热带湿润性季风气候区，多年平均气温１３．５ ℃，多年平均降水量７８５ ｍｍ。地势南高北低，高程２４８ ～ ６５０ ｍ，最长汇流路径９．４ｋｍ，平均坡度１６．２°，平均河段比降２４．７‰。土壤类型为砂黏土（占８６％）和砂壤土（占１４％），土地利用类型为有林地（占７９％）和耕地（占２１％）。流域内建有３２处小型塘堰路坝，总蓄水量超过１０ 万ｍ３。王宗店村位于流域出口，村落现状防洪能力不足１０ ａ 一遇。２０２１ 年７ 月２０ 日流域突发暴雨山洪，专家调查洪水洪峰流量为７６８ ｍ３ ／ ｓ，重现期为２００～３００ ａ［１１］ ，水流平均流速５ ｍ／ ｓ。洪水导致王宗店村２３ 人失踪或遇难。

收集到的基础数据主要有小流域数据、场次雨洪数据和《河南省中小流域设计暴雨洪水图集》。小流域数据包括基于１ ∶ ５０ 万ＤＥＭ、ＤＬＧ 和２．５ ｍ 遥感影像分析提取的小流域划分和属性信息。场次雨洪数据包括研究区周边６ 个雨量站小时尺度的实测降雨数据（２０２１－０７－１８Ｔ８：００—０７－２２Ｔ１２：００）和王宗店水位站１５ ｍｉｎ 尺度的实测水位数据（２０２１－０７－１９Ｔ０：００—０７－２０Ｔ１７：００），均来源于河南省水文局，降雨集中时段（２０２１－０７－２０Ｔ６：００—１７：００）实测雨洪数据见表１，２０日５：００ 前各测站实测累积降雨量为１２９．６ ～ ３３１．０ｍｍ。《河南省中小流域设计暴雨洪水图集》包括河南省暴雨洪水设计成果，来源于河南省水文局。

２ 研究方法

２．１ 流域水文模拟

２．１．１ 中国山洪水文模型

中国山洪水文模型（Ｃｈｉｎａ Ｆｌａｓｈ Ｆｌｏｏｄ ｈｙｄｒｏｌｏｇｉｃａｌｍｏｄｅｌ， ＣＮＦＦ）是由中国水利水电科学研究院研发的分布式水文模型，已广泛应用于全国及各省（区）山洪模拟与预警预报研究［１２－１３］ 。本研究采用初损后损法进行产流计算，采用分布式单位线法进行坡面汇流计算，采用动态马斯京根法进行河道洪水演算。

分布式单位线法应用１ ∶ ５ 万ＤＥＭ（数据网格为２５ ｍ×２５ ｍ）和２．５ ｍ 土地利用和植被信息等高精度地形地貌数据，通过式（１）计算流域内各网格的坡面流流速和汇流时间，经过一次线性水库调蓄得到不同时段的小流域分布式单位线组（１０ ｍｉｎ、３０ ｍｉｎ、１ ｈ）。

式中：Ｖ 为水流速度；Ｋ 为坡面综合流速系数，根据土地利用类型确定［１４］ ；Ｓ 为水力坡降；ｉ 为无因次雨强；Ｌｍ为第ｍ 个网格的水流流路长度；Ｔｊ 为第ｊ 个网格的水流汇集时间；Ｖｍ 为第ｍ 个网格的流速；ｃ ＝ １ 或 ２；Ｍｊ为第ｊ 个网格水流流路上网格的数量。

２．１．２ 模型构建及评估

基于流域ＤＥＭ 及山洪沟分布，研究区共划分为１０ 个小流域单元（见图１），各小流域单元及单元内河道的基本属性见表２。模型参数主要包括产流参数初损Ｉ０、稳定下渗率ｆｃ，演进参数糙率ｎ，马斯京根法参数ｋ、ｘ。Ｉ０、ｆｃ和ｎ 基于场次前期降雨、流域水文下垫面条件等综合确定，ｋ 和ｘ 采用概化的抛物线断面和示储流量动态计算。

模型评估关注对“７·２０”暴雨洪水洪峰的模拟。基于实测水位数据和专家调查洪峰流量，采用洪峰流量相对误差（ＥＱ ）和峰现时间误差（ＴＰ ）对洪峰模拟效果进行评估。指标计算公式如下：

式中：Ｑｍｓ 和Ｑｍｅ 分别为模拟和专家调查洪峰流量，其中Ｑｍｅ ＝ ７６８ ｍ３ ／ ｓ；ＴＱｍｓ 和ＴＺｍｏ 分别为模拟流量过程和实测水位过程的峰现时间。

２．２ 降雨时空情景构建

经计算，“７·２０” 山洪场次汇流时间约为３１．３３ｍｉｎ。依据“雨洪模拟计算步长不应长于场次汇流时间的１／３”的原则，选择以１０ ｍｉｎ 为模型计算步长并对测站小时降雨量插值形成１０ ｍｉｎ 降雨量系列。记最大１ ｈ 降雨（Ｍ６０－ｍａｘ）发生时段为主雨峰时段。对于非主雨峰时段，自降雨发生开始逐３ ｈ 滑动构建累积降雨量—历时之间的回归关系进而实现１０ ｍｉｎ 降雨量插值。对于主雨峰时段，认为场次最大１０ ｍｉｎ 降雨量（Ｍ１０－ｍａｘ）发生在该时段且与Ｍ６０－ｍａｘ 频率相同，通过式（４）对各测站Ｍ１０－ｍａｘ 进行估算。假定Ｍ１０－ｍａｘ 分别发生在主雨峰时段的第２～５ 个１０ ｍｉｎ，结合主雨峰前后时段降雨构建回归关系进行插值，形成４ 种主雨峰时段１０ ｍｉｎ 降雨量分布情景（记为Ｔ２～Ｔ５）。此外，还设置了小时降雨平均分配形成１０ ｍｉｎ 降雨量系列的时间情景（记为ＴＵ），以评估１０ ｍｉｎ 降雨量是否均匀分布对洪水模拟的影响。因此，共构建了５ 种１０ ｍｉｎ 降雨量时间分布情景，即Ｔ２～Ｔ５、ＴＵ。

Ｍ１０－ｍａｘ ＝ ｋＭ６０－ｍａｘ （４）

式中：ｋ 为同频率下Ｍ１０－ｍａｘ与Ｍ６０－ｍａｘ之比。

基于《河南省中小流域设计暴雨洪水图集》计算ｋ在不同设计重现期（５ ～ ２００ ａ） 的取值，并构建ｋ 与Ｍ６０－ｍａｘ的回归关系（见图２），即可基于测站实测Ｍ６０－ｍａｘ查得ｋ 相应取值。

降雨的空间描述方案是影响分布式水文模型模拟精度的重要因素［１５］ 。基于插值得到的测站１０ ｍｉｎ 降雨量，采用常用的泰森多边形法（Ｓ１）、反距离权重法（Ｓ２）和等雨量线法（Ｓ３）计算流域平均降雨量，形成３种降雨量空间分布。考虑降雨时空分布的影响，最终形成１５ 种降雨情景进行洪水模拟影响评估。

２．３ 不确定性来源分解

采用方差分析（Ａｎａｌｙｓｉｓ ｏｆ Ｖａｒｉａｎｃｅ，ＡＮＯＶＡ） 解析各降雨不确定性来源对洪峰模拟的相对影响［１６］ 。ＡＮＯＶＡ 将不同降雨情景驱动下洪峰要素（洪峰流量、峰现时间）模拟结果的不确定性（ＵＦ）分解为源自降雨时间和空间分布（即主效应）及时空分布耦合作用（即交互项）的不确定性，即

式中：Ｙｉ，ｊ为使用第ｉ 种降雨时间情景和第ｊ 种降雨空间情景时洪峰要素的模拟结果；Ｙ －为所有降雨情景下洪峰要素模拟结果的均值；Ｙ －ｉ 和Ｙ －ｊ 分别为使用第ｉ 种降雨时间情景和第ｊ 种降雨空间情景时洪峰要素模拟结果的均值；Ｉ 和Ｊ 分别为降雨时间和空间情景数，本研究中Ｉ ＝５，Ｊ ＝３。

３ 结果与分析

３．１ 降雨情景特征分析

由图２ 可知，ｋ 随最大１ ｈ 降雨量增大而减小。基于测站实测降雨量确定各雨量站的ｋ 值为０．３５３（寺沟） ～０．３８１（盆窑），计算得到雨量站最大１０ ｍｉｎ 降雨量为２０．６（盆窑） ～３３．０ ｍｍ（寺沟）。

鉴于场次汇流时间不足１ ｈ，对１５ 种降雨情景下流域降雨特征的分析重点是峰前１ ｈ 时段，即２０ 日１３：００—１４：００。时段降雨总量主要受降雨空间情景影响，Ｓ１～ Ｓ３ 情景下时段雨量分别为９０．６ ～ ９１．４ ｍｍ、８４．６～８５．５ ｍｍ 和８８．０～８８．３ ｍｍ。总的来看，３ 种空间情景下时段雨量相差不大，其中Ｓ１ 情景降雨量略大于Ｓ２ 和Ｓ３ 的，其原因是泰森多边形法插值结果易受距离较近测站影响，柿树湾雨量站距流域最近且主雨峰较大，导致Ｓ１ 情景下时段流域降雨总量略大。时段降雨时程分布主要受降雨时间情景影响，以采用空间情景Ｓ１ 为例，１３：００—１４：００ 内５ 种时间情景下流域１０ｍｉｎ 降雨量的累积分布见图３。最大１０ ｍｉｎ 降雨量的量级和发生时段不同，导致不同时间情景下降雨的时程分布存在明显差异。

３．２ 场次模拟效果评估

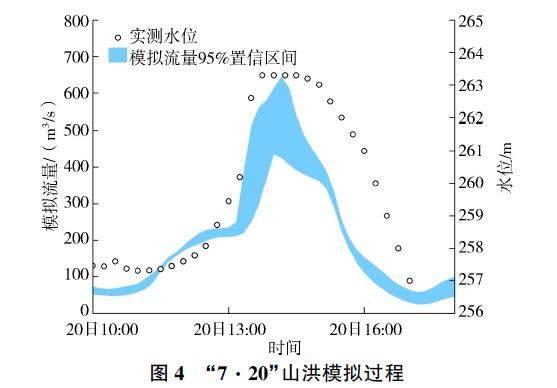
不同降雨情景下洪水模拟结果见表３，“７·２０”山洪模拟过程见图４。１５ 种降雨情景驱动下ＥＱ 为－３６．９７％～－１４．９６％，ＴＰ为－０．３３～０．１７ ｈ，ＣＮＦＦ 较好地再现了场次洪峰流量和峰现时间。当前模型未考虑流域内塘堰路坝溃决的影响，导致模拟得到的洪峰流量略低于专家调查洪峰流量。

３．３ 降雨时空情景对洪峰模拟的影响

“７·２０”暴雨洪水洪峰流量和峰现时间模拟结果见表３。１５ 种情景下模拟洪峰流量Ｑｍｓ为４８４．１～６５３．１ ｍ３ ／ ｓ，模拟峰现时间ＴＱｍｓ 为２０ 日１３：４０～１４：１０。对于洪峰流量而言，不同时间情景下１０ ｍｉｎ 降雨量非均匀分布［３ 种空间情景下Ｔ２～Ｔ５ 与ＴＵ 相比Ｑｍｓ分别增加５１．７～１３３．２ ｍ３ ／ ｓ（Ｓ１）、５０．４～１２３．１ ｍ３ ／ ｓ（Ｓ２）和５０．２～１３１．０ ｍ３ ／ ｓ（Ｓ３）］和最大１０ ｍｉｎ 降雨量發生位置偏后［３ 种空间情景下Ｔ５ 与其余情景相比Ｑｍｓ 分别增加３６．８～１３３．２ ｍ３ ／ ｓ（Ｓ１）、２８．６～１２３．１ ｍ３ ／ ｓ（Ｓ２）和３４．５～１３１．０ ｍ３ ／ ｓ（Ｓ３）］均会形成较大的洪峰流量，体现了短历时峰值降雨的量级和发生时间对山丘区小流域洪峰流量模拟的关键性。不同空间情景下Ｑｍｓ 分布规律与峰前１ ｈ 时段雨量分布规律一致，Ｓ１ 情景下Ｑｍｓ较大，其次为Ｓ３、Ｓ２，Ｓ１ 较Ｓ２、Ｓ３ 的Ｑｍｓ分别增加３５．８～４５．９ｍ３ ／ ｓ、１７．６～２４．３ ｍ３ ／ ｓ。

对于峰现时间而言，不同时间情景下１０ ｍｉｎ 降雨量均匀分布和最大１０ ｍｉｎ 降雨量发生位置偏后均会导致峰现时间较晚，５ 种时间情景下ＴＱｍｓ 分别为１３：４０、１３：５０、１４：００、１４：１０ 和１４：１０。空间情景变化不会引起ＴＱｍｓ 的改变，Ｓ１ ～ Ｓ３ 情景下ＴＱｍｓ 集合均为１３：４０～１４：１０。

３．４ 洪峰模拟不确定性分解

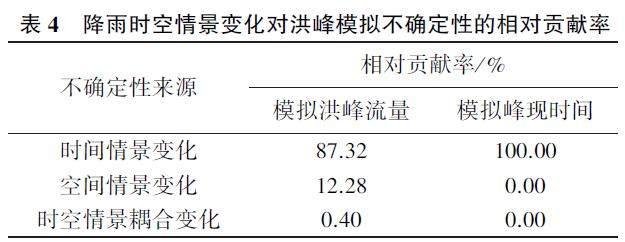
洪峰流量和峰现时间模拟结果的不确定来源相对贡献率见表４。对于Ｑｍｓ而言，降雨时间情景变化是不确定性的最主要来源，相对贡献率为８７．３２％；其次为空间情景变化，相对贡献率为１２．２８％；时空情景耦合变化对模拟不确定性的影响较小，相对贡献率仅为０．４０％。对于ＴＱｍｓ 而言，时间情景变化是模拟结果不确定性的唯一来源，空间情景变化不会影响峰现时间模拟结果。

相较于空间情景变化，降雨时间情景变化是导致王宗店流域“７·２０”事件洪峰模拟不确定性的关键。暴雨山洪产汇流时间短、形成发展速度快，场次洪峰的形成发展与短历时降雨特性密切相关。随着最大１０ｍｉｎ 降雨量级和发生时间的改变，流域模拟洪峰量级和峰现时间均随之显著变化，体现了短历时雨峰特性对山丘区小流域山洪响应模拟的显著影响。王宗店流域面积较小，降雨空间分布的异质性较弱［１７］ ，加之流域周边雨量测站的数量及分布均具有较好的代表性，采用不同的空间插值方法所得到的流域降雨在空间分布和平均量级等方面差别不大，因此不同降雨空间情景下场次洪峰模拟结果基本一致。

４ 结论

本文以河南省荥阳市王宗店流域“７·２０”山洪灾害为例，基于小时尺度实测降雨，综合利用累积降雨量与历时之间的回归关系、设计条件下的雨峰特性和降雨空间插值方法，考虑降雨时空分布变化构建了１５ 种１０ ｍｉｎ 尺度下的降雨输入情景，利用中国山洪水文模型和方差分析理论解析并量化了降雨时空情景变化对洪峰模拟不确定性的影响，主要结论如下：

１）中国山洪水文模型合理地再现了王宗店流域“７·２０”山洪流域洪峰响应过程，１５ 种降雨情景下洪峰流量相对误差为－３６．９７％～－１４．９６％，峰现时间误差为－０．５０～０．１７ ｈ，因未考虑流域内小型塘堰路坝溃决而导致模拟洪峰流量偏低。

２）不同降雨时间情景下，１０ ｍｉｎ 降雨量均匀分布模拟得到的洪峰流量较小、峰现时间较晚。对于非均匀分布的１０ ｍｉｎ 降雨量情景，最大１０ ｍｉｎ 降雨量发生位置越晚，模拟得到的洪峰流量越大、峰现时间越晚。不同降雨空间情景下，采用泰森多边形法插值流域降雨量得到的模拟洪峰流量最大，而模拟峰现时间受空间情景影响较小。

３）降雨时间情景变化是洪峰流量和峰现时间模拟的主要不确定性来源，相对贡献率分别为８７．３２％和１００．００％，空间情景变化和时空情景耦合变化仅影响洪峰流量模拟，相对贡献率分别为１２．２８％和０．４０％。研究区流域面积较小且雨量站空间数量代表性较好，采用不同空间插值方法得到的流域降雨无显著差异，因此降雨空间情景变化对洪峰模拟不确定性影响较小。

今后应进一步收集水文气象条件、地形、下垫面条件等差异显著的山丘区小流域场次雨洪资料，以探究降雨时空变化对次洪模拟不确定性影响的普适规律。

参考文献：

［１］ ＷＥＳＴＲＡ Ｓ，ＴＨＹＥＲ Ｍ，ＬＥＯＮＡＲＤ Ｍ，ｅｔ ａｌ．Ａ Ｓｔｒａｔｅｇｙ ｆｏｒ Ｄｉ?ａｇｎｏｓｉｎｇ ａｎｄ Ｉｎｔｅｒｐｒｅｔｉｎｇ Ｈｙｄｒｏｌｏｇｉｃａｌ Ｍｏｄｅｌ Ｎｏｎｓｔａｔｉｏｎａｒｉｔｙ［Ｊ］．Ｗａｔｅｒ Ｒｅｓｏｕｒｃｅｓ Ｒｅｓｅａｒｃｈ，２０１４，５０（６）：５０９０－５１１３．

［２］ 杨小柳，王艺臻．水文模型的不确定性和异因同果性：认知的回顾［Ｊ］．水利学报，２０１８，４９（１）：１３６－１４３．

［３］ ＺＨＡＩ Ｘ Ｙ，ＧＵＯ Ｌ，ＺＨＡＮＧ Ｙ Ｙ．Ｆｌａｓｈ Ｆｌｏｏｄ Ｔｙｐｅ Ｉｄｅｎｔｉｆｉ?ｃａｔｉｏｎ ａｎｄ Ｓｉｍｕｌａｔｉｏｎ Ｂａｓｅｄ ｏｎ Ｆｌａｓｈ Ｆｌｏｏｄ Ｂｅｈａｖｉｏｒ Ｉｎｄｉｃｅｓｉｎ Ｃｈｉｎａ［Ｊ］．Ｓｃｉｅｎｃｅ Ｃｈｉｎａ Ｅａｒｔｈ Ｓｃｉｅｎｃｅｓ，２０２１，６４（７）：１１４０－１１５４．

［４］ ＢＯＲＧＡ Ｍ，ＡＮＡＧＮＯＳＴＯＵ Ｅ Ｎ，ＢＬ?ＳＣＨＬ Ｇ，ｅｔ ａｌ．ＦｌａｓｈＦｌｏｏｄ Ｆｏｒｅｃａｓｔｉｎｇ， Ｗａｒｎｉｎｇ ａｎｄ Ｒｉｓｋ Ｍａｎａｇｅｍｅｎｔ： ｔｈｅ ＨＹ?ＤＲＡＴＥ Ｐｒｏｊｅｃｔ［Ｊ］．Ｅｎｖｉｒｏｎｍｅｎｔａｌ Ｓｃｉｅｎｃｅ ＆ Ｐｏｌｉｃｙ，２０１１，１４（７）：８３４－８４４．

［５］ ＺＨＯＵ Ｘ Ｄ，ＭＡ Ｗ Ｃ，ＥＣＨＩＺＥＮＹＡ Ｗ，ｅｔ ａｌ．Ｔｈｅ Ｕｎｃｅｒｔａｉｎｔｙｏｆ Ｆｌｏｏｄ Ｆｒｅｑｕｅｎｃｙ Ａｎａｌｙｓｅｓ ｉｎ Ｈｙｄｒｏｄｙｎａｍｉｃ Ｍｏｄｅｌ Ｓｉｍｕｌａ?ｔｉｏｎｓ［Ｊ］．Ｎａｔｕｒａｌ Ｈａｚａｒｄｓ ａｎｄ Ｅａｒｔｈ Ｓｙｓｔｅｍ Ｓｃｉｅｎｃｅｓ，２０２１，２１（３）：１０７１－１０８５．

［６］ 陈华，霍苒，曾强，等．雨量站网布设对水文模型不确定性影响的比较［Ｊ］．水科学进展，２０１９，３０（１）：３４－４４．

［７］ ＳＩＬＶＥＳＴＲＯ Ｆ，ＲＥＢＯＲＡ Ｎ，ＧＩＡＮＮＯＮＩ Ｆ，ｅｔ ａｌ．Ｔｈｅ ＦｌａｓｈＦｌｏｏｄ ｏｆ ｔｈｅ Ｂｉｓａｇｎｏ Ｃｒｅｅｋ ｏｎ ９ｔｈ Ｏｃｔｏｂｅｒ ２０１４：Ａｎ “Ｕｎｆｏｒ?ｔｕｎａｔｅ” Ｃｏｍｂｉｎａｔｉｏｎ ｏｆ Ｓｐａｔｉａｌ ａｎｄ Ｔｅｍｐｏｒａｌ Ｓｃａｌｅｓ ［ Ｊ］．Ｊｏｕｒｎａｌ ｏｆ Ｈｙｄｒｏｌｏｇｙ，２０１６，５４１：５０－６２．

［８］ ＬＩＵ Ｙ Ｈ，ＬＩ Ｚ Ｊ，ＬＩＵ Ｚ Ｙ，ｅｔ ａｌ．Ｉｍｐａｃｔ ｏｆ Ｒａｉｎｆａｌｌ Ｓｐａｔｉｏ?ｔｅｍｐｏｒａｌ Ｖａｒｉａｂｉｌｉｔｙ ａｎｄ Ｍｏｄｅｌ Ｓｔｒｕｃｔｕｒｅｓ ｏｎ Ｆｌｏｏｄ Ｓｉｍｕｌａｔｉｏｎｉｎ Ｓｅｍｉ?Ａｒｉｄ Ｒｅｇｉｏｎｓ［Ｊ］．Ｓｔｏｃｈａｓｔｉｃ Ｅｎｖｉｒｏｎｍｅｎｔａｌ Ｒｅｓｅａｒｃｈａｎｄ Ｒｉｓｋ Ａｓｓｅｓｓｍｅｎｔ，２０２２，３６（３）：７８５－８０９．

［９］ 李大洋，梁忠民，周艳．基于ＭＩＫＥ ＳＨＥ 的洪水模拟与尺度效应分析［Ｊ］．水力发电，２０１９，４５（５）：２８－３３，６６．

［１０］ 肖楠，叶磊，吴剑，等．降雨对山丘区小流域洪峰模拟不确定性的影响［Ｊ］．中国农村水利水电，２０１８（７）：３５－３８，４３．

［１１］ 吴泽斌，万海斌．２０２１ 年河南郑州山区４ 市“７·２０”特大暴雨灾害简析［Ｊ］．中国防汛抗旱，２０２２，３２（３）：２７－３１．

［１２］ 翟晓燕，郭良，刘荣华，等．中国山洪水文模型研制与应用：以安徽省中小流域为例［Ｊ］．应用基礎与工程科学学报，２０２０，２８（５）：１０１８－１０３６．

［１３］ 王雪梅，郭良，翟晓燕，等． 基于中国山洪水文模型（ＣＮＦＦ）的中小流域洪水频率分析［Ｊ］．中国防汛抗旱，２０２２，３２（６）：３１－３５．

［１４］ ＵＳＤＡ－ＳＣＳ．Ｎａｔｉｏｎａｌ Ｅｎｇｉｎｅｅｒｉｎｇ Ｈａｎｄｂｏｏｋ，Ｓｅｃｔｉｏｎ ４，Ｈｙ?ｄｒｏｌｏｇｙ［Ｍ］．Ｗａｓｈｉｎｇｔｏｎ Ｄ Ｃ：Ｓｏｉｌ Ｃｏｎｓｅｒｖａｔｉｏｎ Ｓｅｒｖｉｃｅｓ，ＵＳ Ｄｅｐａｒｔｍｅｎｔ ｏｆ Ａｇｒｉｃｕｌｔｕｒｅ，１９８５：２５－２８．

［１５］ 张雪松，郝芳华，张建永．降雨空间分布不均匀性对流域径流和泥沙模拟影响研究［Ｊ］．水土保持研究，２００４，１１（１）：９－１２．

［１６］ ＶＥＴＴＥＲ Ｔ，ＨＵＡＮＧ Ｓ，ＡＩＣＨ Ｖ，ｅｔ ａｌ．Ｍｕｌｔｉ?ｍｏｄｅｌ ＣｌｉｍａｔｅＩｍｐａｃｔ Ａｓｓｅｓｓｍｅｎｔ ａｎｄ Ｉｎｔｅｒｃｏｍｐａｒｉｓｏｎ ｆｏｒ Ｔｈｒｅｅ Ｌａｒｇｅ?Ｓｃａｌｅ Ｒｉｖｅｒ Ｂａｓｉｎｓ ｏｎ Ｔｈｒｅｅ Ｃｏｎｔｉｎｅｎｔｓ［Ｊ］．Ｅａｒｔｈ ＳｙｓｔｅｍＤｙｎａｍｉｃｓ，２０１５，６（１）：１７－４３．

［１７］ ＨＵＡＮＧ Ｙ Ｃ，Ｂ?ＲＤＯＳＳＹ Ａ，ＺＨＡＮＧ Ｋ．Ｓｅｎｓｉｔｉｖｉｔｙ ｏｆ Ｈｙｄｒｏ?ｌｏｇｉｃａｌ Ｍｏｄｅｌｓ ｔｏ Ｔｅｍｐｏｒａｌ ａｎｄ Ｓｐａｔｉａｌ Ｒｅｓｏｌｕｔｉｏｎｓ ｏｆ ＲａｉｎｆａｌｌＤａｔａ［Ｊ］．Ｈｙｄｒｏｌｏｇｙ ａｎｄ Ｅａｒｔｈ Ｓｙｓｔｅｍ Ｓｃｉｅｎｃｅｓ，２０１９，２３（６）：２６４７－２６６３．

【责任编辑 许立新】

基金项目：国家自然科学基金资助项目（４２１７１０４７）