大型水库运用对河口尾闾河道出汊的影响研究
杨卓媛 夏军强 宋红波 刘国强

摘 要:为定量研究大型水库运用对河口尾闾河道出汊的影响,以黄河口尾闾段为研究对象提出了一种基于改进熵权法的河道出汊阈值确定方法,根据实测水沙资料确定了尾闾河道出汊指标计算公式及相应的河道出汊阈值,在还原无小浪底工程时尾闾段水沙及河槽形态调整过程的基础上,结合出汊阈值对比分析了有、无小浪底工程时尾闾段发生河道出汊概率的差异。结果表明:河段河相系数和汛期平均水流冲刷强度分别为边界和水沙条件中对河道出汊贡献最大的两个指标;黄河口尾闾段河道出汊阈值为38.16,当出汊指标大于38.16 时尾闾段发生河道出汊;小浪底工程运用约束了进入尾闾段的沙量,河道出汊概率明显减小。
关键词:河道出汊阈值;水沙条件;河床调整;黄河口尾闾段;小浪底水库
中图分类号:TV147; TV882.1 文献标志码:A doi:10.3969/ j.issn.1000-1379.2024.04.006
引用格式:楊卓媛,夏军强,宋红波,等.大型水库运用对河口尾闾河道出汊的影响研究[J].人民黄河,2024,46(4):37-42.
黄河口尾闾段河道出汊是河口突然发生局部摆动的一种自然现象,与河道出汊不同的是,黄河口改道指随着河道出汊频率提高,出汊点逐渐向上游移动,最终由河道出汊累积效应触发整条入海流路发生的大幅度河道迁移现象[1-2] 。频繁发生的黄河口尾闾段河道出汊摆动为黄河口改道提供了条件,对出汊河段的上游河势稳定及防洪安全造成了严重威胁[2] ;此外,尾闾段河道出汊摆动导致三角洲岸滩蚀退,植被生境改变,湿地面积严重萎缩[3] 。因此,河道出汊的发生是水沙条件与河床边界条件相互作用的结果[1-2,4] 。小浪底工程位于黄河中游最后一个峡谷段出口,距离黄河口尾闾段起点利津断面约759 km,是黄河干流上最后一个拥有较大库容的控制性工程,对进入黄河口尾闾段水沙条件的影响最为显著[1] 。研究小浪底工程运用对黄河口尾闾段河道出汊的影响,不仅有助于理解河道出汊过程中水沙与河床边界条件之间的相互作用机制,同时也能为黄河下游河道整治工程建设提供有效的科学依据。
国外关于河道出汊阈值的研究多考虑河床边界条件变化,这是因为世界上大多数河口尾闾段河道出汊的时间周期较长(100~1 000a),在构建河道出汊指标时往往忽略天然河流中具有非恒定性的水沙条件[4-5] 。黄河口尾闾段河道出汊的时间周期为10 a 左右,因此上述河道出汊阈值的确定方法并不适用于黄河口尾闾段。国内针对黄河口尾闾段河道出汊阈值已有一定的研究成果,如吉祖稳等[6] 利用1980—1992 年遥感影像资料,分析了黄河口拦门沙区域的沟汊演变特征,结合水沙条件及河床边界条件对黄河口尾闾段河道沟汊的形成机制进行了初步探讨,但未提出有效的尾闾段河道出汊阈值确定方法;茹玉英等[7] 依据来沙量、河床比降、宽深比、平滩流量、河道弯曲系数等参数的组合确定河道出汊概率;王恺忱[8] 将沙嘴长宽比、流量比以及相对滩槽高差的组合作为黄河口尾闾段河道出汊阈值。由于上述研究成果多为定性分析,采用的参数组合较为复杂,因此在实际应用时有较大困难。
小浪底工程是距离黄河口尾闾段最近的大型水利枢纽,其运用改变了进入黄河口尾闾段的水沙条件,近期河段河槽形态的调整过程显著, 并于2004 年、2007 年突然发生南北向大于1 km 的河道摆动,即发生自然河道出汊[9-10] 。目前,合理量化黄河口尾闾段河道出汊阈值,并依此分析小浪底工程运用影响的相关研究较少。本文基于三门峡、小浪底和利津3 站的实测资料,还原1999—2018 年黄河口尾闾段在无小浪底工程运用情况下来水来沙及河床形态调整过程,并结合出汊阈值定量对比分析有、无小浪底工程运用情况下同时期内尾闾段河道出汊概率,以探究小浪底工程对黄河口尾闾段河道出汊的影响。
1 研究河段概况
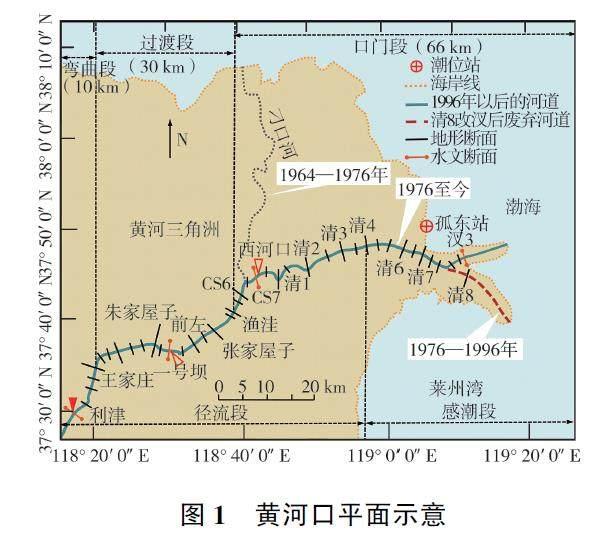
黄河入海口位于莱州湾与渤海湾之间,属于弱潮陆相型河口,潮差沿三角洲海岸分布呈马鞍形,平均潮差1.5 m 左右[1] 。黄河口尾闾段上起利津、下至渤海(见图1),河段总长度约为106 km。按照平面形态差异可将黄河口尾闾段划分为弯曲段、过渡段和口门段3 段。其中:利津—王家庄段长约10 km,为弯曲型河段,河槽较为窄深,滩槽高差较大(为4~7 m),主要河湾得到了控导工程的控制,主槽横向摆动不明显;渔洼以下河段为口门段,长约66 km,河槽宽浅,滩槽高差2~3 m,清4 断面以下无控导工程,河势变化剧烈[11] ;王家庄—渔洼段长约30 km,为过渡型河段,滩槽高差为4~5 m,该段控导工程较少,主槽摆动较为频繁。依据河道内水动力特点可将利津—清4 段划为径流段,清4—口门段划为感潮河段[1] 。从图1 还可以看出,由于1996 年的清8 人工出汊工程实施,因此黄河口清7 以下河段发生了较明显的迁移;1996 年后,黄河口河道开始由原来的东南方向改为朝东北方向延伸,而旧河道向西北方向退缩。以往研究表明,黄河口尾闾段的感潮河段极短,西河口断面已不再受海洋动力的影响[12] 。
2 尾闾段河道出汊阈值的确定
为定量判别尾闾段河道是否会发生出汊,提出一种河道出汊阈值确定方法:首先采用改进的熵权法识别用于构建尾闾段河道出汊指标计算公式的主控因子;然后根据实测资料率定河道出汊指标计算公式,从而获取相应的河道出汊阈值。
2.1 水沙及边界条件指标体系
根据Schumm[13] 提出的河道出汊原理,洪水过程是冲积河流河道出汊的决定性动力因素,而海洋动力(如潮汐、潮流、波浪和风暴潮等)的影响较弱,主要体现在河口侵蚀基准面的变化,对水位的抬升则具有一定的时限,短时间内便会消失。此外,河床边界条件也很大程度上决定了河道出汊时机和位置。因此在研究河道出汊时,河床边界条件和水沙条件应是导致尾闾段河道出汊的两个主控因素。表1 列出了常用于表示河床边界条件和水沙条件的指标,各指标的计算方法详见“指标含义或来源”,其中标有文献来源的指标计算方法可在文献中找到详细的计算过程。
2.2 河道出汊阈值计算步骤
采用信息熵的理论与方法,引入河床演变的指标信息熵和年份、试验组别信息熵概念,结合逻辑回归分析,计算各指标对河道出汊影响权重,步骤如下:
1)构建n 年(或组)m 个指标的初始矩阵Xαβ =(xαβ )(α =1,2,…,n;β =1,2,…,m)。
2)指标归一化处理。由于各个指标所表征对象的量纲和数量级大小都不相同,因此为了排除量纲及数量级大小不同造成的影响,需要对原始数据(实测值)进行归一化处理,归一化公式为
式中: x?αβ 为第α 年第β 个指标的归一化值, xαβ 为第α年第β 个指标的原始值,max(xβ )、min(xβ )分别为第β个指标的最大、最小原始值。
3)根据尾闾段的实测数据及试验数据资料,采用逻辑回归分析方法,对β 个指标X 与河道出汊编码Y(河道發生出汊编码为1,未发生出汊编码为0)进行回归分析,分析得到河道出汊发生的概率P:
式中:Pαβ为第α 年(或组)第β 项指标值在第α 年(或组)各指标中所占比例,Eβ为第β 个指标的信息熵。
5)计算指标的权重:
式中: wβ 为第β 个指标的权重。
本研究选取对应水沙条件相关指标为5 种,即m =5;对应河床边界条件相关指标为6 种,即m = 6。由式(4)得到所有水沙条件和河床边界条件相关指标对尾闾段河道出汊的权重,若? 为河床边界条件中权重最大的指标, ψ 为水沙条件中权重最大的指标,则?和ψ 即为河道出汊主控因子。河道出汊指标计算公式为
? = aψb (5)
式中:a、b 为待定参数,需通过河道实际观测数据和试验数据进行率定。
引入Swamee 等[17] 用于评估界线方程可靠性的参数λ :
式中:λ 为界线参数,Nc为处于坐标系中正确分界区域的点数,Nw 为处于坐标系中错误分界区域的点数,Nt为总点数。
通过调整式(5)中的待定参数a 和b,使得分布在正确分界区域的点数Nc最多,同时控制错误分界区域中点数Nw的增加。当λ 取值大于0.5 时,可认为该河道出汊界线方程准确合理[17] 。
在λ>0.5 的前提下对式(5)进行变形,得到河道出汊指标计算公式的最终形式:
ACI= ?ψ -b < a (7)
式中:ACI(Avulsion Criterion Index)为河道出汊指标,a为河道出汊阈值。
ACI 值越大表明发生河道出汊的可能性越大,当ACI≥a 时表示尾闾段河道发生出汊。河道出汊指标的物理含义为:当河床稳定性差异不大时,水流运动强度越大的河段越接近河道出汊阈值;在相同的水流运动强度下,河床稳定性越差的河段越接近河道出汊阈值,即越容易发生出汊。
2.3 尾闾段河道出汊阈值
19 组物理模型试验数据与1996—2018 年黄河口尾闾段实测水沙及地形资料,为黄河口尾闾段河道出汊指标计算公式的率定提供了有效的数据基础[15] 。由表2 给出的信息熵E 值和权重w 计算结果可知,对黄河口尾闾段河道出汊影响最大的河床边界条件是河段河相系数ξbf( w = 0.356)、影响最大的水沙条件是汛期平均水流冲刷强度Ff( w =0.383),即河道出汊主控因子为ξbf和Ff,因此采用这两个指标构建尾闾段河道出汊指标计算公式。需要注意的是,根据以往研究[10] ,本文对于“汛期平均”的概念,采用黄河口尾闾段7—9 月相关实测数据的平均值。
由计算结果可得河道出汊界线方程形式为
式(8)中F f表示河道内水流运动强度和河道输沙能力[16] ,ξbf则表征河床横向稳定性及河岸可动性[17] 。当河床横向稳定性变差时更容易发生河道出汊,即相同F f下ξbf值位于阈值界线上方表示发生河道出汊,位于界线下方表示未发生河道出汊。基于黄河口尾闾段1996—2016 年实测水沙地形数据及19 组黄河口概化物理模型试验数据,得到40 组河相系数与水流冲刷强度数据。图2 点绘了河相系数—水流冲刷强度关系,可以看到数据点出现了明显的分界。
率定式(8)得到a、b(λ =0.74):
式中:下标YRE 为Yellow River Estuary 缩写,表示“黄河口”。
黄河口尾闾段河道出汊阈值aYRE 为38. 16,当ACIYRE≥38.16 时黄河口发生尾闾段河道出汊。
3 工程运用对近期尾闾段河道出汊的影响
已有研究对黄河口尾闾段在2003—2007 年的水沙条件、河道边界条件进行了详细的对比分析[10] 。本文主要通过对比有、无小浪底工程两种工况下近期黄河口尾闾段河道出汊概率的差异,研究小浪底工程运用的影响:首先计算利津站在无小浪底工程时的汛期水沙数据;然后估算相应的河槽形态;最后计算两种工况下1999—2018 年尾闾段河道出汊指标逐年变化情况,对比分析有、无小浪底工程运用情况下同时期黄河口尾闾段河道出汊概率。
3.1 无小浪底工程时的汛期流量及输沙率
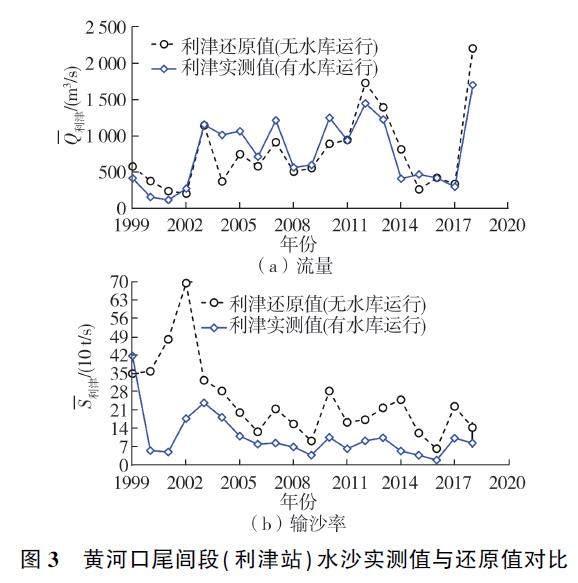
小浪底水库蓄水前三门峡、小浪底和利津3 站的汛期平均流量之间、输沙率之间具有良好的线性关系(R2 >0.9)。选取1986—1999 年三门峡、小浪底和利津三站的汛期平均流量和输沙率建立回归关系,根据回归关系进一步还原:1)1999—2018 年利津站在无小浪底工程运用时的汛期平均流量,将其与有小浪底工程运用时的实测汛期平均流量进行对比[见图3(a)],由图3(a)可以看出,1999—2001 年、2012—2014 年和2018 年的流量还原值大于实测值,其他年份实测值较大;2)1999—2018 年利津站在无小浪底工程运用时的汛期平均输沙率与有小浪底工程运用时的实测汛期平均输沙率进行对比[见图3(b)],由图3(b)可以看出,有小浪底工程运用时利津站的汛期平均输沙率明显减小。
3.2 无小浪底工程时平滩河槽形态变化比较
为探究小浪底工程运用对黄河口尾闾段河槽形态调整将产生怎样的影响,将1999—2018 年利津站的还原水沙数据代入尾闾段平滩河槽特征指标与前4 a 汛期平均水流冲刷强度的关系式[9] ,得到在无小浪底工程运用的情况下黄河口尾闾段平滩特征指标的变化过程。图4 对比了同一时期黄河口尾闾段平滩河槽特征指标[9](包括河段平滩流量Q bf、平滩水深H bf、平滩面积A bf与平滩河宽B bf)实测值与还原值。从图4 中可以看出,小浪底工程运用对黄河口尾闾河段平滩水深H bf、平滩面积A bf的影响较为明显[见图4(a)、图4(c)],这2 个指标相较无工程运用情况下均明显偏小。此外,无工程运用情况下的河段平滩河宽B bf和平滩流量Q bf[9] 在2016—2018 年调整幅度较大[见图4(b)、图4(d)],而有工程运用时这2 个指标呈迅速增大的趋势。从整体上看,小浪底工程运用一定程度上改善了黄河口尾闾段河槽形态及过流能力。
3.3 有、无小浪底工程时尾闾段河道出汊概率比较
依据还原的利津站汛期水沙数据及黄河口尾闾段平滩河槽特征指标变化过程,计算得到1999—2018 年黄河口尾闾段水流冲刷强度Ff 及河相系数ξbf 的还原值,然后代入河道出汊指标计算公式便可得到无工程运用时黄河口尾闾段河道的ACI 值(如ACI′YRE )。图5 对比了1999—2018 年在有、无小浪底工程运用时黄河口尾闾段河道ACI 值。当有小浪底工程时,黄河口尾闾段河道ACI 值大于河道出汊阈值(38.16)的年份集中在2003—2007 年,共计5 a 发生河道出汊的概率较高[见图5(a)];当无小浪底工程时,黄河口尾闾段河道ACI 值大于河道出汊阈值的年份则分布较分散,在1999—2000 年、2003—2006 年、2012—2013 年和2018 年(共计9 a) 发生河道出汊的概率较大[见图5(b)]。
上述研究表明,小浪底工程运用将尾闾段河道出汊概率减小了近50%,主要原因在于:以往巨大的来沙量使天然状态下的黄河口尾闾段淤积严重,导致出汊现象频频发生,1999 年以前尾闾段河道出汊多发生于来沙量较大的年份[2,6,15] ;小浪底工程的运用有效减少了进入尾闾段的沙量,使尾闾段的水沙条件得以改善,该河段因此由持续淤积状态转为持续冲刷状态,故小浪底工程的运用能够显著减小黄河口尾闾段河道出汊概率。
4 结论
1)基于黄河口23 a 实测水沙数据、地形数据及19组物理模型试验数据,计算得到河段河相系数和汛期平均水流冲刷强度分别为河床边界条件和水沙条件中对河道出汊贡献权重最大的两个指标(权重分别为0.356、0.383),由此确定了河道出汊主控因子。
2)河道出汊阈值确定方法能有效获取黄河口尾闾段河道出汊阈值。以河段河相系数和汛期平均水流冲刷强度间关系为基础建立了河道出汊界线方程,从而得到了黄河口尾闾段河道出汊阈值为38.16。
3)通过对比有、无小浪底工程运用情况下黄河口尾闾段水沙及河床形态的实测数据和还原结果,发现小浪底工程运用显著改善了尾闾段河槽形态、提高了过流能力、降低了黄河口尾闾段河道出汊概率。
参考文献:
[1] 余欣,王万战,李岩,等.小浪底水库运行以来黄河口演变分析[J].泥沙研究,2016,41(6):8-11.
[2] 余欣,吉祖稳,王开荣,等.黄河河口演变与流路稳定关键技术研究[J].人民黄河,2020,42(9):66-70,129.
[3] 李燕妮,李鹏,吴晓,等.黄河口湿地时空变化过程及其主控因素[J].海洋地质与第四纪地质,2022,42(1):68-80.
[4] SINHA R,SRIPRIYANKA K,JAIN V,et al.Avulsion Thresholdand Planform Dynamics of the Kosi River in North Bihar(India) and Nepal:A GIS Framework [J]. Geomorphology,2014,216(7):157-170.
[5] ZHENG S,WU B S,WANG K R,et al.Evolution of the YellowRiver Delta,China:Impacts of Channel Avulsion and Progra?dation[J].International Journal of Sediment Research,2017,32(1):34-44.
[6] 吉祖稳,胡春宏.黄河口口门地区沟汊形成机制初探[J].泥沙研究,1996,21(4):96-102.
[7] 茹玉英,王开荣,侯志军.黄河口河道对小浪底水库运用的响应[J].泥沙研究,2008,33(3):63-68.
[8] 王恺忱.对当前黄河下游河道演变发展的认识[J].人民黄河,2022,44(3):40-43,47.
[9] 杨卓媛,夏军强,周美蓉,等.黄河口尾闾段河床形态调整及过流能力变化[J].水科学进展,2019,30(3):305-315.
[10] 杨卓媛,夏军强,周美蓉,等.黄河口尾闾河道近期自然出汊过程及其机理探讨[J].泥沙研究,2022,47(1):65-72.
[11] 王万战,张世安,NITTROUER J A.黄河河口段河道糙率计算方法[J].人民黄河,2018,40(12):4-8.
[12] 王开荣,黄海军,张永平.黄河清水沟流路河口尾闾段河床形态萎缩特征[J].海洋地质与第四纪地质,2008,28(2):15-22.
[13] SCHUMM S A.The Fluvial System[R].New York:John Wi?ley & Sons,1977:246-264.
[14] XIA J Q,LI X J,LI T,et al.Response of Reach?Scale Bank?full Channel Geometry to the Altered Flow and SedimentRegime in the Lower Yellow River [ J]. Geomorphology,2014,213(4):255-265.
[15] 夏军强,吴保生,王艳平.近期黄河下游河床调整过程及特点[J].水科学进展,2008,19(3):301-308.
[16] LI J,XIA J Q,ZHOU M R,et al.Variation in Reach?ScaleThalweg?Migration Intensity in A Braided Reach of theLower Yellow River in 1986 - 2015 [ J]. Earth SurfaceProcesses and Landforms,2017,42:1952-1962.
[17] SWAMEE P K,OJHA C S P.Criteria for Evaluating FlowClasses in Alluvial Channels[J].Journal of Hydraulic Engi?neering,1994,120(5):652-658.
【责任编辑 简 群】
基金項目:国家重点研发计划项目(2021YFC3200202)

