基于用户密度和平均访问时间的边缘服务器放置方法

胡春节 刘静 郑文祥

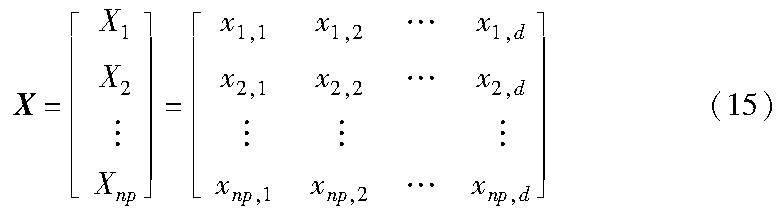
摘 要：为解决边缘服务器放置过程中资源浪费和延迟增加的问题，对边缘服务器放置方案的用户密度和平均访问时间进行分析建模，将其描述为多目标优化问题。设计了一种基于用户密度和平均访问时间的边缘服务器放置方案，并提出了一种多目标海马遗传算法（MOSGA）解决该问题。MOSGA首先使用多目标优化算法的思想对海马优化（sea horse optimizer，SHO）算法进行改进，使SHO算法能够适用于多目标优化问题，并在此基础上使用遗传算法改进SHO算法的繁殖操作，使MOSGA能更好地跳出局部最优解，加速问题的求解。该算法在上海电信数据集上进行了实验验证，仿真实验结果表明，MOSGA明显优于RA、K-means、NSGA、LMM，不仅有效解决了服务器资源浪费的问题，同时大大降低终端设备访问服务器的时间。

关键词：边缘计算；边缘服务器放置；多目标优化；海马优化；遗传算法

中图分类号：TP393   文献标志码：A    文章编号：1001-3695（2024）05-024-1448-08

doi： 10.19734/j.issn.1001-3695.2023.09.0413

Edge server placement method based on user density and average access time

Abstract：To address the issue of resource wastage and increasing latencies in the placement process of edge servers， this paper analyzed and modeled the user density and average access time of edge server placement schemes as multi-objective optimization problems. It designed an edge server placement scheme based on user density and average access time， and proposed a multi-objective sea-horse genetic algorithm （MOSGA） to solve this problem. The MOSGA algorithm firstly used the idea of multi-objective optimization algorithm to improve the SHO algorithm， so that the SHO algorithm could be applied to multi-objective optimization problems. It used the genetic algorithm to improve the propagation operation of the SHO algorithm， so that the MOSGA could better jump out of the local optimal solution and accelerate the solution of the problem. The proposed algorithm was verified on the data set of Shanghai Telecom， and the simulation experiment results show that MOSGA is obviously better than RA， K-means， NSGA and LMM， which not only effectively solves the problem of server resource waste， but also greatly reduces the time of terminal equipment to access the server.

Key words：mobile edge computing; edge server placement; multi-objective optimization; sea horse optimizer; genetic algorithm

0 引言

隨着5G网络的推广和普及，移动边缘计算（mobile edge computing，MEC）作为一种新兴的计算模式，引起人们的广泛关注。MEC的主要特点是缩短终端用户设备和计算、存储资源之间的距离，提供低延迟和高带宽的服务，从而提升用户体验。边缘服务器（edge server，ES）的放置位置是影响MEC性能的一个关键因素。

然而，设计一个好的边缘服务器放置（edge server placement，ESP）方案是一个艰巨的任务，存在以下困难：a）需要充分利用ES的计算和存储资源，避免某些ES过于闲置而出现资源浪费；b）MEC的目标是降低网络延迟和提高系统的响应速度，因此在选择ESP的位置时，必须尽量减少数据传输时间和平均访问时间；c）ESP放置问题是一个NP难问题（non-deterministic polynomial-time hard，NP-hard），例如从100个基站中选择20个放置位置，其可能的方案约为5.36×1020种，这就意味着对这个问题求解的搜索空间将是巨大的，难以在短时间内找到最优解，需要设计一种高效的算法进行求解。

近年来，MEC备受关注［1～5］，而ESP问题则是该领域亟待解决的问题。在求解ESP问题时，现有各项研究工作的关注点也不同。一些研究关注于降低延迟或者平衡边缘服务器负载，例如文献［6］基于免疫优化算法设计了一种有效的ESP方法，旨在减少访问延迟并优化负载；文献［7］针对车联网出现额外的延迟和网络拥塞现象，提出了一种动态边ESP方法，以适应车联网交通动态变化；文献［8］研究了智能城市移动边缘计算环境中的ESP问题，以优化移动边缘计算网络性能，提高响应速度；文献［9］将ESP问题建模为一个容量聚类问题进行求解，最大限度地减少回程延迟。文献［10］设计了一种负载感知的ESP方法，以保证边缘服务的执行效率，降低访问延迟；文献［11］考虑到ES出现故障的不确定性，研究了用于边缘计算的鲁棒性服务器布局问题，旨在最大化预期总体工作负载。以上方法在一定程度上解决了ESP问题，但忽视了ES一旦放置将难以移动的特点，这直接影响到边缘服务器计算和存储资源的利用率。

另一些研究的关注点在降低ES的能耗或成本方面。例如，文献［12］设计一种双因子近似算法，用于解决异构ESP问题，从而保证有界的延迟和放置成本；文献［13］提出了一种跨区域资源优化模型，旨在最小化服务提供商的成本，并得到最终ESP策略；文献［14］研究了MEC中最小化微云的放置成本和端到端延迟成本问题，并提出了基于成本意识的微云放置算法；文献［15］研究了具有能量感知的ESP问题，并设计了一种基于粒子群优化的能量感知ESP算法来寻找最优解，目标是最小化ES的放置成本。但是文献［12］的双因子近似算法存在求解精度不高的问题，而文献［13～15］未考虑终端用户对延迟要求。此外，上述研究将ESP问题建模为单目标或加权单目标优化问题，优化单个目标通常难以适应多样化的应用场景和用户需求。而将多个目标加权成单目标优化的方法虽然可以将多个优化指标转换为一个综合指标，但会存在优化目标权重难以确定、目标之间相互影响等问题。

元启发式算法因为高效性、灵活性、可扩展性、鲁棒性和可解释性等诸多优点［16，17］被用于求解ESP问题。例如文献［18］提出一个基于改进的非支配排序遗传算法（non-dominated sorting genetic algorithm，NSGA）来解决网络分区和边缘服务器放置问题，以优化边缘计算在分布式状态估计中的应用。

此外，半监督学习的聚类算法也被用求解ESP问题。例如文献［19］提出了一种基于改进的K均值聚类的方法（K-means clustering algorithm，K-means）来确定ES的理论位置和数量，以此优化ES的网络延迟、能耗和成本。

针对ES放置问题中存在的困难和上述研究方案中的不足，本文提出了一种基于用户密度和平均访问时间的边缘服务器放置方法，并设计了一种元启发式算法——多目标海马遗传算法（multi-objective seahorse genetic algorithm，MOSGA）求解ES放置方案。本文的贡献如下：

a）建立了MEC的系统模型，相比其他研究工作，本文对用户密度和平均访问时间进行分析建模，并将ESP问题描述为多目标优化问题。考虑用户密度和平均访问时间的影响，能够更好地满足用户需求并解决ESP过程中的资源浪费问题。此外，将ESP问题描述为多目标优化问题，可适应更多元化的应用场景和用户需求，同时也能解決将多个优化目标加权为一个目标优化时，优化目标权重难以确定、目标之间相互影响等问题。

b）提出了一种多目标海马遗传算法求解ES放置方案，旨在解决ESP问题求解规模大、复杂度高的问题。MOSGA结合多目标优化算法（multi-objective optimization algorithm，MOP）［20］的思想改进SHO算法［21］，使得MOSGA可以用于解决多目标优化问题，在此基础上使用遗传算法（genetic algorithm，GA）［22］改进SHO算法的繁殖阶段，使得MOSGA能更好地跳出局部最优，加快问题的求解。

c）仿真实验结果表明，MOSGA与随机算法（random algorithm，RA）、聚类算法K-means［19］ 、非支配遗传算法NSGA［18］、拉格朗日乘数法（lagrange multiplier method，LMM）［23］相比，不仅在总的用户密度和平均访问时间方面表现最优，有效减少了服务器的资源浪费，而且大大降低了终端设备访问服务器的时间。

1 系统模型和问题定义

1.1 系统模型

MEC的体系结构有云数据中心层、边缘层和用户设备层三个层次。本文的研究集中在边缘层，该层由N个基站组成，本文的目标是在这些基站中选择M个合适的位置放置ES，使得用户设备的请求可以在离用户更近的ES上被处理，用户设备请求中部分数据处理和存储任务可以转移到ES上处理，降低延迟的同时减少对网络传输带宽的需求，节约资源，为用户提供更好的体验。

1.2 城市基站访问记录

在城市中的基站每时每刻都会接收来自用户设备的请求，产生源源不断的访问记录，假定在一段时间内共产生K条访问记录，每条接入记录中包含访问开始时间tstri、访问结束时间tendi、基站编号bidi以及用户设备编号uidi四个属性。

1.3 用户密度模型

在一段时间内基站i接入的用户设备数量Euclid Math OneNApi计算方式为

对于任意一个基站i，其覆盖面积Ai计算如下：

Ai=πr2i（3）

其中：ri为基站i的覆盖半径。那么对于任意一个基站i，其用户密度Ui计算如下：

1.4 平均访问时间模型

在一段时间内，基站i被访问的总时间Ti计算方式如下：

其中：［bidj=i］表示当第j条访问记录的基站编号bidj等于i时为1，否则为0；tendj表示第j条访问记录的结束访问时间；tstrj表示第j条访问记录的开始访问时间。

对于任意一个基站i，其被访问的总次数Ci计算如下：

其中：［bidj=i］表示当第j条访问记录的基站编号bidj等于i时为1，否则为0。那么，对于任意一个基站的i平均访问时间Tavei计算为

1.5 服务质量模型

在MEC中，在基站上放置ES的目的是为了尽可能缩短计算和存储资源与用户之间的距离，降低延迟，为用户提供更好的体验。换句话说，ES放置位置选址应当满足以下两点：

a）ES的放置位置尽可能选择用户密集的基站。用户密集的基站往往承载着较多的用户请求。这可能会占用大量的网络传输带宽资源，在这些基站上放置ES可以将部分请求分流到ES上进行处理，减轻基站的压力，提高基站的处理能力和稳定性，节约资源。同时在这些基站上放置ES也能缩短用户设备与服务器之间的距离，降低网络延迟，提高用户体验。

b）ES的放置位置尽可能选择用户设备平均访问时间长的基站。用户设备在访问基站时，由于基站的负载较大和被访问时间较长，可能会面临较长的等待时间和较高的访问延迟。通过在这些基站上放置ES，可以将用户的请求分配到离用户更近的服务器上进行处理，减少访问延迟和等待时间，提高服务的质量和可用性，从而提高用户体验。

因此，给定M个ES，从N个基站中选择出M个位置放置ES，其总的用户密度F1和总的被访问时长F2分别计算如下：

根据以上描述，该问题用数学语言描述如下：

其中：式（11）表示i和j的取值均为正整数且满足1≤i≤N，1≤j≤K；式（12）表示一个基站上最多只能放置一个ES；式（13）表示被选中放置ES的基站数量要等于ES数量M；式（14）是用户设备访问时间限制，即每条访问记录的访问开始时间tstrj不超过访问结束时间tendj。

2 边缘服务器放置

基于用户密度和平均访问时间的ES放置方法可以再表述如下：

a）找到一个最优的边缘服务器放置问题解决方案X。

b）使其满足式（11）～（14）的约束并且最大化式（10）。

2.1 NP-hard问题证明

定理1 基于用户密度和平均访问时间的边缘服务器放置问题Q是一个NP-hard问题。

證明 通过对0-1背包问题［23］的简化，本文可以将问题Q归约到一个已知的NP-Hard问题。具体地，本文将每个基站i看作一个物品Bi，每个物品Bi有一个价值Wi（F1，F2），Ui为

由于0-1背包问题是已知的NP-hard问题，所以问题Q也是NP-hard问题，即没有已知的多项式时间算法可以解决。这意味着在一般情况下，本文无法在多项式时间内找到问题Q的最优解，而只能通过启发式算法或近似算法来求解。

根据以上证明可以得出结论：基于用户密度和平均访问时间的边缘服务器放置问题Q是NP-hard问题。

2.2 问题编码和算法设计

为了有效地解决ESP问题，本文提出了一种基于用户密度和平均访问时间的边缘服务器放置方法，并设计了一种MOSGA算法求解该问题。

SHO算法最早由Zhao等人［21］提出，其灵感来自于海马的移动、捕捉和繁殖行为，具有速度快、收敛精度高等优点。由于SHO算法提出之初是用于解决单目标优化问题，而本文要解决的问题是一个多目标优化问题，所以不能直接应用。为了解决这一问题，本文将SHO算法与MOP算法结合，使其能够用于解决多目标优化问题，同时为使SHO算法能够更好地跳出局部最优，加快问题的求解，本文使用GA算法改进SHO算法的繁殖行为。下面将详细介绍MOSGA。

1）海马个体和适应度函数的构造

在MOSGA中，每个海马实际上代表一种解决方案。整个海马种群被定义为

其中：np为海马的种群大小；d为变量的维数。对于所有的海马，其适应度值存储如下：

2）海马的移动

海马的移动行为用于实现解空间的探索和开发，其有两种模式：

a）海马伴随着海洋中的旋涡螺旋运动，这时新海马的位置如下：

X1new（t+1）=Xi（t）+Lévy（λ）（（Xelite（t）－Xi（t））×x×y×z+Xelite（t））（17）

其中：Xelite（t）为当前迭代次数下最优海马时，并由算法4得出，Xi（t）为第i个海马；x、y、z分别表示在螺旋运动下坐标（x，y，z）的三维分量，x=ρ×cos（θ），y=ρ×sin（θ），z=ρ×θ，这里ρ=u×eθv；u、v的取值均为0.05、λ取值为1.5［21］，θ为［0，2π］的随机数；Lévy（z）为莱维飞行函数，其计算方式如下：

其中：s为一个常数；w、k为 ［0，1］的随机数，由式（19）得出。σ的计算方式如下：

b）海马随着海浪做布朗运动，新海马的位置如下：

X1new（t+1）=Xi（t）+rand×l×βt×（Xi（t）－βt×Xelite）（20）

其中：Xelite为全局最优海马的位置；l为一个常数；βt为布朗游走系数，计算方式为

由于海马的移动服从正态0-1分布，为了权衡搜索和开发的性能，当rand（0，1）>0，海马随着海洋中的旋涡螺旋运动，否则海马随着海浪做布朗运动。

算法1 海马移动时位置的更新过程

3）海马的捕食

海马以捕食浮游动物和小型甲壳动物为生，捕食有成功和失败两种结果。当海马捕食成功时，海马的位置更新如下：

X2new（t+1）=α×（Xelite－rand×X1new（t））+（1－α）×Xelite（22）

当海马捕食失败时，海马的位置更新如下：

X2new（t+1）=（1－α）×（X1new（t）－rand×Xelite）+α×X1new（t）（23）

其中：X1new（t）表示海马在第t次运动后的新位置；α表示海马捕食的步长，计算方式如下：

其中：T表示最大迭代次数。

海马进行捕食时，有90%的概率捕食成功，当海马捕食成功时，按照式（22）更新位置；否则，按照式（21）更新位置。

算法2 海马捕食时位置的更新过程

4）海马的繁殖

与其他动物的繁殖不同，雄性海马负责繁殖。首先，根据适应度函数进行非支配排序，将适应度好的一半海马个体作为雄性海马，另一半作为雌性海马。海马角色分配过程计算如下：

fa=X2sort（1：np/2）（25）

mo=X2sort（np/2+1：np）（26）

其中：X2sort是按适应度降序排列的种群； fa和mo分别表示雄性和雌性海马群。当雌性个体交配产生后代时，为了使得算法能够更好地跳出局部最优解，本文使用GA为海马的繁殖行为添加变异操作，交配后的个体有一定的概率突变。海马进行繁殖时：

Xoffi=rXfai+（1－r）Xmoi（27）

xoffi，q=lb+r1（ub－lb）（28）

其中，式（27）表示海马交配产生后代Xoffi；式（28）表示后代Xoffi，q发生变异；r和r1为（0，1）的随机数；Xoffi，q表示后代i在第q维发生变异；q为 ［0，d］的随机整数；ub、lb问题变量的上界和下界。

算法3 海马繁殖行为

5）最佳海马个体

由于SHO算法提出之初是用于解决单目标优化问题，而本文的问题是一个多目标优化问题，为了使SHO算法能够解决多目标问题，受MOP算法的启发，本文使用MOP算法的非支配排序策略来比较个体的优劣，并计算最高等级种群的质心，选择离质心最近的个体作为最佳海马：a）将海马种群分为多个层；b）计算最高等级层中海马适应值的质心；c）计算该层所有海马个体与质心欧氏距离；d）选择离质心最近的海马的位置作为最佳海马的位置。

算法4 最佳海马位置寻找过程

6）MOSGA整体设计

在MOSGA中，海马有移动、捕食和繁殖三种行为。MOSGA的完整流程为：a）初始化海马种群的位置X、当前迭代次数t、最佳白鲸位置Xelite；b）开始种群迭代过程，计算当前迭代次数下所有海马个体适应值f1（Xi（t））、f2（Xi（t）），运行算法4计算当前迭代次数下最佳海马位置Xelite（t），并更新全局最佳海马位置Xelite；c）运行算法1和2更新海马位置，运行算法3产生子代海马，并将父子代海马合并；d）检查海马位置并修复，再次计算海马群的适应值，根据适应值对X（t）非支配排序，选择排名前np的海马个体进入X（t+1），更新迭代次数；e）检查终止条件，当t≥T，MOSGA终止；否则返回b）；f）计算最佳海马位置Xelite及其适应值f1（Xelite（t））、f2（Xelite（t））。

算法5 MOSGA

2.3 MOSGA时间复杂度分析

时间复杂度是判断算法性能的一个重要指标。本节将对MOSGA的时间复杂度进行分析。假设种群数量为np，最大迭代次数为T。MOSGA的时间复杂度来自以下五部分：

a）海马群的初始化，其时间复杂度为O（np）；

b）根据算法4寻找最佳海马个体的时间复杂度为O（2×np2×T）；

c）海马移动执行算法1的时间复杂度为O（np×T）；

d）海马捕食执行算法2的时间复杂度为O（np×T）；

e）海马繁殖执行算法3的时间复杂度O（2×np2×T）。

因此，MOBGA总的时间复杂度可以计算如下：

O（np）+2×O（2×np2×T）+2×O（np×T）=O（4np2×T+np×T）≈O（np2×T）（29）

即MOSGA的时间复杂度可近似为O（np2×T）。

3 仿真和评估

3.1 实验环境

硬件环境：CPU为Intel Core i7 3.20 GHz，RAM为32 GB。

软件环境：操作系统为64位Windows 11；开发软件为PyCharm；編程语言为Python；编程工具为Python 3.9.7；数据库为MySQL 5.7.23。

3.2 数据集说明

本文使用上海电信真实数据集对算法性能进行验证，由于原始数据集中部分数据字段值缺失，所以需要对原始数据集进行处理后才能使用。经过处理后得到的数据集合包含6 270个移动用户在2 770个基站上共计558 737条访问记录，每条记录包括基站经纬度、用户标识号、访问开始时间和访问结束时间。为了便于处理分析这些数据，本文将这些数据写入MySQL数据库中。

3.3 对比算法

为了验证MOSGA的性能。本文将与RA、K-means［19］、NSGA［18］、LMM［23］进行对比。此外，为了保持公平性，MOSGA与对比算法中NSGA的最大迭代次数保持相同的设置。

由于LMM是基于的凸优化理论来求解优化问题的，而凸优化理论要求目标优化函数和解空间是凸的，适用于凸问题、单目标问题、光滑问题。本文所建模的问题是多目标优化问题，且优化函数非凸。为了使LMM可用于求解本文的问题，本文将多目标优化问题近似分解成P1和P2两个单目标优化问题，分解如下：

其中：问题P1为最大化基站的平均访问时间；问题P2为最大化基站的用户密度；C1为放松约束后所有基站上ES总数最大值的不等式约束；C2为选中放置ES的基站数量要等于ES数目的等式约束。问题P1、P2的拉格朗日函数形式如下：

L1（X，β1，φ1）=－f1（X）+β1h（X）+φ1g（X）（34）

L2（X，β2，φ2）=－f2（X）+β2h（X）+φ2g（X）（35）

其中：β1、β2、φ1、φ2均为拉格朗日乘子。约束条件为

通过求解满足式（36）约束的多组候选ESP方案X，过滤掉不满足式（14）访问时间约束的方案，并使用算法4中的寻找最佳海马的策略选择出使用了LMM求解出的最优ESP方案。

3.4 实验参数设置

本文实验参数设置表1所示。

为了测试算法在不同任务数目和任务最大完成时间约束下的性能。本文设置了四组对比实验，每组实验重复20次取平均值。

a）第一组实验：基站数量为2 770，边缘服务器数量从50增加到450，间隔为50，测试在不同边缘服务器数量下算法的性能；

b）第二组实验：边缘服务器数量为50，基站数量从500增加到1 400，间隔为100，测试在不同基站数量下算法的性能；

c）第三组实验：边缘服务器数量为50，基站数量为2 770，根据3.5节网络延迟的测试数据，将每跳路由平均往返延迟设置为2 ms，以此测试不同算法在降低延迟方面的性能。

d）第四组实验：边缘服务器数量为50，基站数量为2 770。测试NSGA和MOSGA在不同迭代次数下算法的收敛性。并以此设置表1中的最大迭代次数。

3.5 实验结果分析

1）不同边缘服务器数量下算法的性能

表2、3记录了在不同边缘服务器数量下算法的性能数据，图2、3展示了在不同边缘服务器数量下算法的性能变化情况。随着边缘服务器数目增多，五种算法在总用户密度和总平均访问时间方面都有增加。其中，MOSGA取得了最优的结果，并且随着边缘服务器数量的增加，其优势表现得尤为明显。这是因为随着边缘服务器数量的增加，有更多的用户密度高且平均访问时间长的基站可供选择，在这种情况下，MOSGA因为求解速度快、收敛精度高和较强的跳出局部最优的能力，可在给定迭代次数下探索到更优秀的放置方案。相比之下，RA的性能取决于随机生成解；K-means的性能在很大程度上依赖于初始聚类中心点；NSGA在探索全局最优点的能力稍显不足；LMM在处理非凸函数时会陷入局部最优解而无法得到全局最优解，因为非凸函数存在多个局部极小值点，同时全局最优解也可能不满足或者部分满足式（36）中的约束，这使得LMM的性能进一步下降。综上所述，MOSGA表现最优。在用户密度方面，RA、K-means、NSGA、LMM与MOSGA的平均性能差距分别为40.37%、23.80%、11.33%、24.37%；在总的平均访问时间方面，RA、K-means、NSGA、LMM与MOSGA的平均性能差距分别为29.94%、15.17%、6.25、20.80%。

2）不同的基站数目下算法的性能

表4和5记录了在不同基站数量下算法的性能数据，图4和5展示了在不同基站数量下算法的性能变化情况。随着基站数量增加，除RA外，其他四种算法在总用户密度和总的平均访问时间方面都有增加。值得注意的是，随着基站数量的增多，这四种算法在总用户密度和总的平均访问时间方面增长较为缓慢，这是因为虽然可选基站的数量在不断增多，但新增的基站并没有更多被选中的潜力，进而导致总的用户密度和总的平均访问时间增长缓慢，但MOSGA的变异操作为其搜索增加了多样性，避免陷入局部最优解，有更大的可能性找到全局最优解。而RA由于其随机性，其效果取决于每一次生成的解。综上所述，MOSGA表现最优。在用户密度方面，RA、K-means、NSGA、LMM与MOSGA的平均性能差距分别为59.42%、27.46%、6.85%、29.21%；在总的平均访问时间方面，RA、K-means、NSGA、LMM与MOSGA的平均性能差距分别为39.58%、22.35%、12.01%、23.08%。

3）不同算法在降低延迟方面的性能

如图6所示，基站接受其覆盖范围内终端设备的计算请求，并通过漫长的路由将计算任务发送到服务器上进行处理。为了评估不同边缘服务器放置算法在降低延迟方面的性能，本文在同一个基站下向7个不同的服务器发送500次大小300 KB的数据包，并以此计算每跳路由之间的网络延迟。表6记录了通过同一基站向不同服务器发送数据的往返延迟。

由表6可知，每跳路由的平均延迟在［1.5，3.5］ms，当边缘服务器放置到基站上時，可减少终端设备到服务器之间的路由跳数，降低延迟（降低的延迟=用户设备的访问频率×路由跳数×平均每跳延迟）。为了便于比较，本文将路由跳数统一设置为1跳，平均每跳延迟设置为2 ms。表7记录了不同边缘服务器放置算法在降低延迟方面的性能。可以看出，MOSGA在降低延迟方面表现最优，RA、K-means、NSGA、LMM与MOSGA的平均性能差距分别为57.65%、9.08%、3.30%、11.99%。

4）不同迭代次数下算法的稳定性

如图7所示当迭代次数大于400时，NSGA、MOSGA已经收敛。根据实验结果，在3.4节将最大迭代次数设置为400。

4 结束语

本文研究了基于用户密度和平均访问时间的ESP问题，并设计了一种高效的算法MOSGA进行求解。MOSGA使用MOP算法的思想改进SHO算法，使其可以用于解决多目标优化问题，同时使用GA改进SHO算法的繁殖阶段，使MOSGA具有更好的全局搜索能力和收敛性，仿真实验结果表明，MOSGA能够有效地优化边缘服务器的放置方案，减少服务器的资源浪费现象，并降低终端设备访问服务器的时间，此项研究可为研究ESP问题提供借鉴。此外，本文未考虑终端设备请求的异构性，若用于新环境，该方法的准确性和效率会有一定的下降，未来本文将探索在终端设备异构情况下的ESP问题，并进一步结合其他领域解决方案的优点进一步改进MOSGA的性能，例如，使用凸优化理论指导MOSGA种群的生成。同时本文也将结合更多的因素进行边缘服务器的放置位置选择，以进一步提升ES放置方案的性能。

参考文献：

［1］Mansouri Y，Babar M A. A review of edge computing： features and resource virtualization ［J］. Journal of Parallel and Distributed Computing，2021，150（1）： 155-183.

［2］Kong Xiangjie，Wu Yuhan，Wang Hui，et al. Edge computing for Internet of Everything： a survey ［J］. IEEE Internet of Things Journal，2022，9（23）： 23472-23485.

［3］谷曉会，章国安. 移动边缘计算在车载网中的应用综述 ［J］. 计算机应用研究，2020，37（6）： 1615-1621. （Guo Xiaohui，Zhang Guoan. Survey of mobile edge computing applications in vehicular network ［J］. Application Research of Computers，2020，37（6）： 1615-1621.）

［4］Jiang Qinting，Zhou Xuanhong，Wang Ruili，et al. Intelligent monitoring for infectious diseases with fuzzy systems and edge computing： a survey ［J］. Applied Soft Computing，2022（123）： 108835-108850.

［5］施巍松，张星洲，王一帆，等. 边缘计算： 现状与展望 ［J］. 计算机研究与发展，2019，56（1）： 69-89. （Shi Weisong，Zhang Xingzhou，Wang Yifan，et al. Edge computing： state-of-the-art and future directions ［J］. Journal of Computer Research and Development，2019，56（1）： 69-89.）

［6］Chen Xiao，Liu Wei，Chen Jing，et al. An edge server placement algorithm in edge computing environment ［C］// Proc of the 12th International Conference on Advanced INFOCOM Technology. Piscataway，NJ： IEEE Press，2020： 85-89.

［7］Shen Bowen，Xu Xiaolong，Qi Lianyong，et al. Dynamic server placement in edge computing toward Internet of Vehicles ［J］. Computer Communications，2021，178（6）： 114-123.

［8］Cao Kun，Li Liying，Cui Yangguang，et al. Exploring placement of heterogeneous edge servers for response time minimization in mobile edge-cloud computing ［J］. IEEE Trans on Industrial Informatics，2020，17（1）： 494-503.

［9］Agac G，Baki B，Ar I M，et al. A supply chain network design for blood and its products using genetic algorithm： a case study of Turkey ［J］. Journal of Industrial and Management Optimization，2023，19（7）： 5407-5446.

［10］Xu Xiaolong，Xue Yuan，Qi Lianyong，et al. Load-aware edge server placement for mobile edge computing in 5G networks ［C］// Proc of the 17th International Conference on Service-Oriented Computing. Cham： Springer，2019： 494-507.

［11］Lu Dongyu，Qu Yuben，Wu Fan，et al. Robust server placement for edge computing ［C］// Proc of IEEE International Parallel and Distributed Processing Symposium. Piscataway，NJ： IEEE Press，2020： 285-294.

［12］Bhatta D，Mashayekhy L. A bifactor approximation algorithm for cloudlet placement in edge computing ［J］. IEEE Trans on Parallel and Distributed Systems，2022，33（8）： 1787-1798.

［13］Xiao Kaile，Gao Zhipeng，Wang Qian，et al. A heuristic algorithm based on resource requirements forecasting for server placement in edge computing ［C］// Proc of Symposium on Edge Computing. Piscataway，NJ： IEEE Press，2018： 354-355.

［14］Fan Qiang，Ansari N. On cost aware cloudlet placement for mobile edge computing ［J］. IEEE/CAA Journal of Automatica Sinica，2019，6（4）： 926-937.

［15］Li Yuanzhe，Wang Shangguang. An energy-aware edge server placement algorithm in mobile edge computing ［C］// Proc of International Conference on Edge Computing. Piscataway，NJ： IEEE Press，2018： 66-73.

［16］趙畅，刘允刚，陈琳，等. 面向元启发式算法的多无人机路径规划现状与展望 ［J］. 控制与决策，2022，37（5）： 1102-1115. （Zhao Chang，Liu Yungang，Chen Lin，et al. Research and development trend of multi-UAV path planning based on metaheuristic algorithm ［J］. Control and Decision，2022，37（5）： 1102-1115.）

［17］Bhol S，Sahu N C. Decarbonizing the grid by optimal scheduling of solar PV-wind turbine-pumped hydro storage considering application on heuristic algorithms： a comprehensive review ［J］. International Journal of Energy Research，2021，45（13）： 18473-18497.

［18］Yuan L，Gu Jie，Ma Jinghuan，et al. Optimal network partition and edge server placement for distributed state estimation ［J］. Journal of Modern Power Systems and Clean Energy，2022，10（6）： 1637-1647.

［19］Li Wenzao，Chen Jiali，Li Yiqian，et al. Mobile edge server deployment towards task offloading in mobile edge computing： a clustering approach ［J］. Mobile Networks and Applications，2022，27（4）： 1476-1489.

［20］Tan K C，Lee T H，Khor E F. Evolutionary algorithms for multi-objective optimization： performance assessments and comparisons ［J］. Artificial Intelligence Review，2002，17（4）： 251-290.

［21］Zhao Shijie，Zhang Tianran，Ma Shilin，et al. Sea-horse optimizer： a novel nature-inspired meta-heuristic for global optimization problems ［J］. Applied Intelligence，2023，53（10）： 11833-11860.

［22］Srinivas M，Patnaik L M. Genetic algorithms： a survey ［J］. Computer，1994，27（6）： 17-26.

［23］Li Mengmou. Generalized Lagrange multiplier method and KKT conditions with an application to distributed optimization ［J］. IEEE Trans on Circuits and Systems Ⅱ： Express Briefs，2018，66（2）： 252-256.

［24］Karp R M. Reducibility among combinatorial problems ［M］. Berlin： Springer，2010： 219-241.

［25］Fei Weilin，Liu Cong，Hu Sheng. Research on swarm intelligence optimization algorithm ［J］. The Journal of China Universities of Posts and Telecommunications，2020，27（3）： 1-20.