甘肃及邻区基于地震预警参数τc和Pd的震级快速计算模型研究
柴文锐 郭晓 张璇 杜建清 张磊 张卫东 蒲举

摘要:地震預警作为目前能够有效减轻地震灾害的手段之一,可以在破坏性地震动来临之前提供几秒至几十秒的预警时间,提醒预警区域采取紧急处置措施以减轻人员伤亡和财产损失。地震预警是一个复杂的系统,其中利用地震参数快速、准确地进行实时震级估算是其有效发挥减灾作用的关键。文章基于2012—2020年发生在甘肃省及邻区的190个地震共821条记录(3.1≤M≤6.6),计算分析在P波1~10 s时间窗长度内,两种地震预警参数(卓越周期τc和位移幅值Pd)分别在垂直向、水平向和三分向均值测项三种不同条件下与峰值参数PGV、PGD的相关性,拟合相应的预警震级快速计算模型,并将估算震级ME与实际震级MC进行比较。结果表明:时间窗长度的改变对结果有一定的影响,而测项改变造成的差别较小。此外,在拟合度、预测残差均值和标准差,以及残差分布等预测效果方面,采用参数Pd的模型性能优于参数τc。考虑到参数和震级的实时计算以及预警信息发布的时效性要求,推荐在该地区应用垂直向记录P波到时3 s后的参数Pd来进行地震预警震级实时快速计算。
关键词:地震预警; 预警参数; 峰值参数; 震级快速计算模型
中图分类号: P315.3 文献标志码:A 文章编号: 1000-0844(2024)03-0703-11
DOI:10.20000/j.1000-0844.20230627001
Fast magnitude estimation model for Gansu and adjacent regions based on earthquake early warning parameters τc and Pd
CHAI Wenrui1,3, GUO Xiao1,2,3, ZHANG Xuan1,3, DU Jianqing1,3, ZHANG Lei3, ZHANG Weidong3, PU Ju3
(1. Lanzhou Institute of Seismology, CEA, Lanzhou 730000, Gansu, China;2. Gansu Lanzhou Geophysics National Observation and Research Station, Lanzhou 730000, Gansu, China;3. Gansu Earthquake Agency, Lanzhou 730000, Gansu, China)
Abstract: Earthquake early warning (EEW) systems—as effective tools for seismic hazard mitigation—offer advance alerts several to tens of seconds before the onset of destructive ground motions, prompting the deployment of emergency measures to minimize casualties and property losses. Specifically, these intricate systems rely on rapid and precise real-time magnitude estimations based on EEW parameters for disaster mitigation. To accelerate magnitude estimation speeds, considering 821 records of 190 earthquakes (3.1≤M≤6.6) that struck the Gansu Province and surrounding regions from 2012 to 2020, we examine the correlation between two EEW parameters (characteristic period τc and displacement amplitude Pd) and peak parameters (peak ground velocity and displacement) under varying conditions: vertical component, horizontal component, and mean value of the three components of a P-wave at 1-10 s. Subsequently, it establishes a fast calculation model for early warning magnitude estimations. Finally, the estimated magnitudes (ME) are compared with those recorded by the China Earthquake Networks Center (MC). Results reveal that while changes in time window durations influence the estimation outcomes, variations in P-wave components exert negligible effects. Moreover, the Pd-based model outperforms the τc-based model in predicting the fitting degree, mean value, and standard deviation of the predicted residuals, as well as the residual distribution. Thus, considering the time scale of real-time parameters, magnitude estimations, and the requirement of timely EEW information release, applying the Pd-based model after 3 s of vertical P-wave arrival is recommended for rapid real-time magnitude estimations by EEW systems in the study area.
Keywords:earthquake early warning; early warning parameters; peak parameters; fast magnitude calculation model
0 引言
地震预警主要是利用地震中携带信息的P波传播速度快于携带能量的S波以及电磁波速度远大于地震波的特点,由部署在监测区的台站接收地震P波并发送至数据处理中心,数据处理中心快速进行实时震级、位置、烈度等参数计算,并在破坏性地震波到达预警区域之前發布预警信息,从而有效减少人员伤亡和财产损失。地震预警这一概念最早由美国学者Cooper[1]在1868年提出,但受制于当时的科技水平,这一想法并未实现。到了20世纪60年代,日本国家铁路JNR开始建设紧急地震探测报警系统UrEDAS[2-3],在铁轨沿线每隔20~25 km安装地震仪,当地震动强度超过40 cm/s2时铁路系统就会发出警报并关闭列车电源,避免脱轨并造成伤亡。1985年墨西哥城发生M8.1地震,造成了约4万人伤亡,此事促进了墨西哥城地震预警系统SAS的建设[4]。该系统利用平均分布在格雷罗海岸的12套加速度地震计组成的台网进行地震预警,成为全球第一套公开发布信息的预警系统。位于马尔马拉断层附近的伊斯坦布尔长期面临着地震高发风险,1999年伊兹米特M7.4和杜兹采M7.2地震之后,该地区安装了100多台强震动记录仪,组成了伊斯坦布尔地震快速反应系统IERRS和预警系统IERREWS[5],利用P波峰值加速度(Peak Ground Acceleration,PGA)和累计绝对速度(Cumulative Absolute Velocity,CAV)发布预警信息。另外,美国南加州和中国台湾也是较早开展地震预警系统建设和应用的主要地区。
总体而言,一套完整的地震预警系统应包括实时地震定位、震级计算、烈度估计以及预警信息发布等几个部分,其中利用地震波初始信息快速进行预警震级测定是其中最关键且最困难的技术环节,震级测定的准确与否将会对后续的预警信息发布和目标区地面运动估计产生极为重要的影响。因此,建立稳定可靠的预警震级计算模型是地震预警系统成败的关键。针对预警震级计算模型,目前多国学者已开展了大量研究工作[6-13]。
1988年,Nakamura[3]研究了地震震级与地震波频率之间的关系,并提出了利用实时速度记录计算卓越周期的方法,该方法已被应用到日本UrEDAS地震预警系统中。Allen等[14]在Nakamura研究的基础上对该算法进行改进,计算得到了实时地震动的卓越周期τp(i),并发现τp(i)的最大值τpmax与震级存在一定关系,该方法也被称为卓越周期法。随后,Kanamori[15]又在卓越周期法的基础上用固定积分区间代替逐步积分区间,得到了特征周期(Characteristic Period,τc)法,并发现τc参数与震级M同样存在一定的相关性[16]。Wu等[17-19]发现,对位移记录进行2阶巴特沃斯滤波后,固定时间窗内的极值(Peak Displacement,Pd)与峰值速度(Peak Ground Velocity,PGV)及震级M间均有较好的相关性,该方法即为Pd方法。Festa等[20]发现在固定区间内对速度平方积分得到的辐射参数IV2与地震释放的能量直接相关,可以用该参数来进行震级预测。上述方法在数学意义上均属于经验(统计)方法,存在一定的离散性,同时受场地条件的影响,这些方法也存在明显的区域特性。为了更好地发挥预警系统的减灾效果,利用某特定区域地震数据研究并建立适合于该区域的震级计算方法和模型就显得尤为重要。
甘肃及邻区处于青藏板块东北缘上,地质构造复杂,地震活动频繁,地震灾害对经济社会发展和人民生命财产安全的潜在威胁长期存在。该区域历史上发生过多次8级以上地震,地震风险相当严重。为有效提高区域地震灾害防范能力,2015年甘肃省建设完成了兰州地震预警示范系统,2018—2023年又开展了国家地震烈度速报与预警工程甘肃子项目建设,预计2023年底建设完成后对社会公众提供预警信息服务。为保证上述预警系统产出信息的准确性和有效性,有必要利用甘肃及邻区的地震数据有针对性地研究并建立适合本区域的预警震级计算模型。
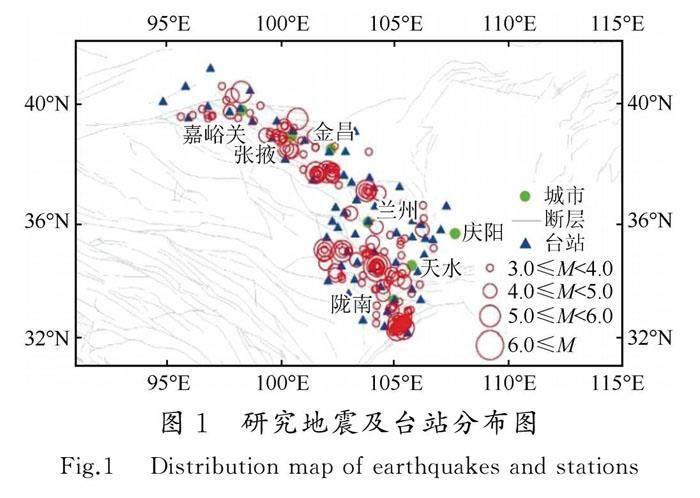
基于上述分析,本文收集了甘肃省及邻区2012—2020年190个地震共821条记录数据(图1),重点围绕以下两个方面展开分析:特征周期τc与峰值速度PGV,峰值位移(Peak Ground Displacement,PGD)的相关性,及其与震级M的拟合;位移幅值Pd与峰值参数PGV、PGD的相关性,及其与震级M的拟合。通过计算分析,得到该区域内由预警特征参数进行震级快速计算的模型,并将上述成果应用到甘肃省地震预警系统中,以期提高预警震级测定的准确性和可靠性,确保预警系统真正发挥减灾实效。
1 待估算参数
本文选取了应用最为广泛的2个预警特征参数来研究其与震级之间的相关性,分别为:P波卓越周期τc和位移幅值Pd。
1.1 周期参数τc
Nakamura[3]最早提出了P波卓越周期的概念,Allen等[14]和Kanamori等[15]在其基础上进行了相关研究,得到如下计算公式:
τpi=Xi/Yi (1)
式中:Xi=αXi-1+x2i;Yi=αYi-1+dxdt2i;xi为速度纪录;α为平滑参数,一般取0.999。
Nakamura后来证明了从地震记录的卓越频率(fP)能够识别地震的大小。根据Parseval定律,fP定义为强震振幅比,可由下式得到:
fP=
式中:U(f)是地震位移时间序列u(t)的傅里叶转换。
随后Kanamori[15]对式(2)进行了改进,将积分上限设为τ0≈3 s,得到:
fPKanamori≈12π∫τ002(t)dt∫τ00u2(t)dt=1τc (3)
式中:u(t)为高通滤波后的位移值;(t)为位移微分后的速度值。Wu等[21]发现,震级M与τc对数间存在较好的线性相关性,即:
M=alg(τc)+b (4)
式中:a和b为待估算参数。
目前,參数τc已被应用到部分国家和地区的地震预警系统中用于震级估算[22-25]。
1.2 位移参数Pd
Wu等[21]在研究中发现,初始位移幅值的峰值Pd与震级大小间同样存在较好的关联,因此可以用来进行震级估算,该方法目前已在台湾[26]和南加州[27]等地区测试成功。震级M、震源距R和Pd对数间的关系如式(5)所示:
M=alg(Pd)+bR+c (5)
式中:a、b和c为待估算参数。
国外其他学者对于Pd与震级间的相关性也进行了深入探讨[27-28],分析发现P波在3 s时间窗长度下的位移幅值Pd与震级M具有较好的相关性,且在M到达7级之前未出现震级饱和现象。因此该参数也被广泛应用于许多国家和地区的地震预警系统中[22,29-30]。
2 数据处理
本文的地震记录全部来自甘肃地震预警台网,时间跨度为2012—2020年,地震观测仪器为100 Hz采样率的三分向速度型地震计。地震记录数据的筛选标准为:(1)震源距R≤100 km;(2)震级M≥3.0;(3)地震事件的记录台站≥3个。最终得到的数据集包含了震级范围为M3.1~6.6的190个地震共821条记录,如图2所示。
对于筛选出来地震记录,采取如下步骤进行数据处理和计算:
(1) 人工读取各次地震事件的P波到时;
(2) 对速度记录进行基线校正并积分,求得相应的位移记录;
(3) 对速度纪录和位移记录进行2阶巴特沃斯滤波,滤波频带范围为0.075 Hz高通滤波;
(4) 依次计算记录数据的垂直向、水平向和三分向均值测项在1~10 s时间窗长度下的τc和Pd参数值。
3 计算结果
3.1 参数τc
(1) τc与峰值参数的相关性
在进行震级拟合之前,首先评估τc与峰值参数PGV、PGD之间的相关性。分别计算各记录数据垂直向、水平向和三分向均值(以下图表中简称均值)测项在1、2、3、4、5、7和10 s时间窗下τc与峰值参数PGV、PGD的皮尔逊相关系数 (Pearson Correlation Coefficient,PCC),统计结果如表1所列。
由表1可以看出,τc与峰值参数PGV、PGD的相关性整体较低(0.15≤PCCτc-PGV≤0.32,0.13≤PCCτc-PGD≤0.29),二者之间的相关性与时间窗长度的变化有关联,随着窗长的增加,不同测项条件下相关系数值均逐渐增加;但测项改变引起的相关系数值变化相对较小。
(2) τc-震级拟合
根据式(4)中的模型形式,拟合了τc与震级M的关系式。不同条件下τc与震级M的拟合曲线如图3所示,拟合关系式中的模型参数值列于表2。由图3和表2发现,不同测项时拟合结果的一致性较好,说明测项改变对拟合结果的影响相对较小。另外,由表2还可以看出,随着时间窗长度的增加,不同测项下的平均绝对误差Mean(-ME-MC-)与标准偏差σ的变化均较小,数值基本稳定,而相关系数PCC在逐步增大,因此增加τc的时间窗长度对震级估算结果有一定的影响,但影响较小。这一结论与Heidari[31]、Sasani[32]、周昱辰等[33]和彭朝勇等[34]的研究结果类似。
为了检验拟合结果的有效性,文中计算了预测残差(估算震级ME与真实震级MC的差值)的均值(表2),并绘制了残差的散点分布及频数分布图(图4,以垂直向测项为例)。从图中可看到,预测残差大部分位于[-1,1]区间内,且整体上服从正态分布。
3.2 参数Pd
(1) Pd与峰值参数的相关性
与τc类似,本文也分析了Pd与峰值参数PGV、PGD之间的相关性。垂直向、水平向和三分向均值测项在1~10 s时间窗下Pd与PGV、PGD的PCC值计算结果如表3所列。由表3可得,Pd与PGV、PGD的相关性整体较高(0.51≤PCCPd-PGV≤0.75,0.76≤PCCPd-PGD≤0.92),随着窗长的增加,不同测项条件下相关系数值均逐渐增加;另外,由测项改变引起的相关性变化主要发生在1~4 s时间窗内,5 s后不同测项时相关系数值结果较为一致。
(2) Pd参数震级拟合
根据式(5)中的模型形式,拟合了Pd与震级M的关系式。不同条件下Pd与震级M的拟合曲线如图5所示,拟合关系式中的模型参数值如表4所列。与τc-M拟合结果类似,不同测项时Pd-M拟合结果的一致性较好,测项改变对拟合结果的影响相对较小。另外,从表4可以看出,随着时间窗长度的增加,不同测项下的平均绝对误差Mean(-ME-MC-)与标准偏差σ均表现出减小的趋势,说明增加Pd的时间窗长度对震级预测性能有一定的提高。
计算出采用Pd进行震级估算的预测残差均值(表4),并绘制了残差的散点分布及频数分布图(图6,以垂直向测项为例)。从图中可看到,预测残差大部分位于[-0.5,0.5]区间内,且整体上服从正态分布。相较于使用τc进行震级估算时的预测残差(图4),使用Pd得到的预测残差分布更为集中。
4 分析与讨论
根据前文的计算结果,分析发现:
(1) 时间窗长度的改变对于τc和Pd与峰值参数的相关性,及震级拟合结果有一定影响,尤其是采用Pd进行震级拟合时。通常来讲,地震发生后破裂会持续一段时间,震级越大,持续时间越长。在本文选取的1~10 s时间窗长度内,随着窗长的增加,τc和Pd与峰值参数的相关性逐渐增加,震级估算的预测残差均值和标准差逐渐减小,拟合结果愈发准确。因此,预警震级计算是一个实时动态更新的过程。考虑到预警震级的准确性及信息发布的迫切性,本文建议使用P波触发后3 s时间窗长度的记录数据进行首次震级估算。
(2) 测项改变对于τc和Pd与峰值参数的相关性,及震级拟合结果影响较小。整体来看,无论是τc,还是Pd,分别采用记录数据的垂直向、水平向和三分向均值测项时,同一时间窗内τc、Pd与PGV、PGD的相关系数值差别不大,模型参数的拟合结果较为一致,基本处于同一数量值水平,预测效果也较为相近。考虑到预警信息的高时效性要求,采用水平向或三分向结果可能会浪费一定的时间,因此实际使用时宜优先采用垂直测项所得的震级计算模型,水平向和均值测项可作为参考和备用选项。
(3) 进行震级计算时,Pd的性能明显优于τc。以垂直测项为例(图7,时间窗长度为3 s),τc与震级M,峰值参数PGV、PGD的相关性整体较弱,随着时间窗的增加,相关系数值逐渐变大,但均小于0.5;Pd与M和PGV、PGD具有较强的相关性,1~10 s时间窗内,Pd-M之间的相关系数均处于0.7左右,Pd-PGV之间的相关系数处于0.57~0.74之间,Pd-PGD之间的相关系数处于0.76~0.81之间(3 s时间窗以后,Pd与PGV、PGD的相关系数值较之前有较大幅度增加)。另外,Pd所得震级估算模型的预测残差大部分位于[-0.5,0.5]之间,τc方法所得模型的预测残差大部分位于[-1,1]之间。无论在拟合度,还是残差均值、标准差、残差分布等预测效果方面,Pd所得模型的性能均优于τc。综合考虑,认为采用Pd并使用垂直向记录所得的震级计算模型性能最优,实际应用中建议优先使用。
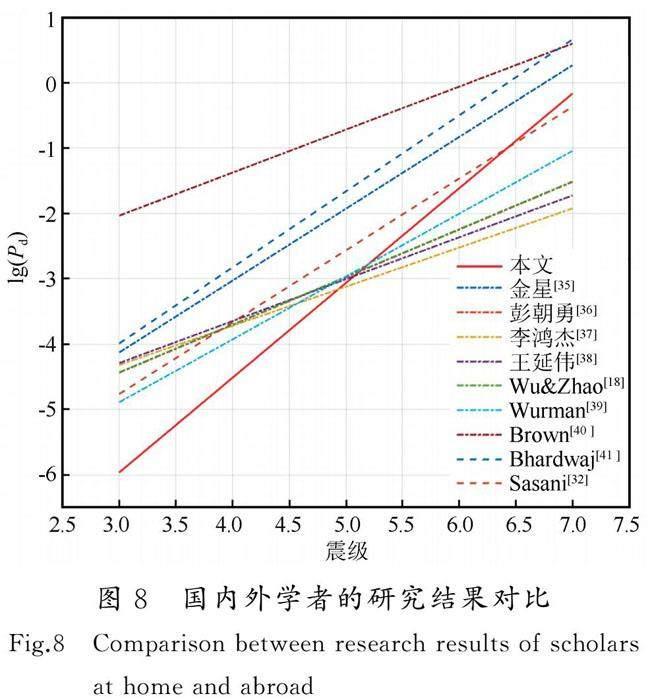
为了分析区域差异对震级估算模型的影响,本文还将国内外不同学者的研究结果进行了比较(表5)。以Pd参数3 s时间窗长度下垂直向记录得到的拟合模型为例进行对比,结果如图8所示。
由图8可以看到,本研究得到的震级估算模型与其他学者的模型结果存在一定差异,对于不同的Pd值,各模型预测的震级结果高低不同。由于不同学者研究的区域及数据来源各不相同,因此得到的模型参数也有所区别,这也进一步证实了在不同区域应用不同的地震预警震级估算模型的必要性。
5 结论
本文以提高预警震级测定的准确性和可靠性为目标,采用2012—2020年發生在甘肃省及邻区的190个地震,共821条记录(3.1≤M≤6.6)为数据源,计算分析了在P波1~10 s时间窗长度内,两个初始地震波特征参数(特征周期τc和最大位移幅值Pd)分别在垂直向、水平向和三分向均值测项三种不同条件下与峰值地震动参数PGD,PGV的相关性,及与震级M的拟合结果,得到适用于甘肃及邻区的地震预警震级快速计算模型,并对模型的预测效果进行了评估和比较。结果表明:时间窗长度的增加对于τc、Pd与峰值参数的相关性,及震级拟合结果均有一定的影响(采用Pd进行震级拟合时受时间窗长度的影响更为明显),但测项改变造成的差别较小;此外,在拟合度、预测残差均值和标准差,以及残差分布等预测效果方面,采用Pd的模型性能明显优于τc。故本研究推荐在该地区使用垂直向记录P波到时3 s后的Pd来进行地震预警震级实时快速计算。
需要说明的是,本文的预警震级快速计算模型结果由甘肃省及邻区的地震记录数据分析得到,由于不同地区整体地质状况和地震波特性的不同,该模型结果与根据其他地区地震记录数据得到的模型结果存在一定的差异。因此,模型结果在推广应用时应慎重考虑其适用性。
致谢:感谢甘肃地震预警台网提供的地震记录数据。
参考文献(References)
[1] COOPER J D.Earthquake indicator[N].San Francisco Daily Evening Bulletin,1868-11-03(5).
[2] NAKAMURA Y.Development of earthquake early-warning system for the Shinkansen,some recent earthquake engineering research and practice in Japan[C]//Proceedings of Japanese National Committee of the International Association for Earthquake Engineering.Tokyo, Japan:[s.n.],1984:224-238.
[3] NAKAMURA Y.On the urgent earthquake detection and alarmsystem[C]//Proceedings of the 9th World Conference on Earthquake Engineering.Tokyo,Japan:[s.n.],1988:673-678.
[4] ARANDA J M E,JIMENEZ A,IBARROLA G,et al.Mexico city seismic alert system[J].Seismological Research Letters,1995,66(6):42-53.
[5] ERDIK M,FAHJAN Y,OZEL O,et al.Istanbul earthquake rapid response and the early warning system[J].Bulletin of Earthquake Engineering,2003,1(1):157-163.
[6] 单新建,尹昊,刘晓东,等.高频GNSS实时地震学与地震预警研究现状[J].地球物理学报,2019,62(8):3043-3052.
SHAN Xinjan,YIN Hao,LIU Xiaodong,et al.High-rate real-time GNSS seismology and early warning of earthquakes[J].Chinese Journal of Geophysics,2019,62(8):3043-3052.
[7] 赵国峰,李卫东,李丽,等.基于国产密码的地震预警服务系统防篡改框架设计与应用[J].地震工程学报,2023,45(1):145-152.
ZHAO Guofeng,LI Weidong,LI Li,et al.Design and application of a tamper-proof framework for the earthquake early warning service system based on domestic cryptographic algorithms[J].China Earthquake Engineering Journal,2023,45(1):145-152.
[8] CUA G,FISCHER M,HEATON T,et al.Real-time performance of the virtual seismologist earthquake early warning algorithm in southern California[J].Seismological Research Letters,2009,80(5):740-747.
[9] WU Y M.A virtual subnetwork approach to earthquake early warning[J].Bulletin of the Seismological Society of America,2002,92(5):2008-2018.
[10] PENG H,WU Z,WU Y M,et al.Developing a prototype earthquake early warning system in the Beijing capital region[J].Seismological Research Letters,2011,82(3):394-403.
[11] ZHANG H C,JIN X,WEI Y X,et al.An earthquake early warning system in Fujian,China[J].Bulletin of the Seismological Society of America,2016,106(2):755-765.
[12] 孫常青,朱振家,潘章容,等.甘肃地震预警测站典型异常波形的频谱分析[J].地震工程学报,2023,45(3):614-624.
SUN Changqing,ZHU Zhenjia,PAN Zhangrong,et al.Spectrum analysis of the typical abnormal waveforms of earthquake early warning stations in Gansu Province[J].China Earthquake Engineering Journal,2023,45(3):614-624.
[13] 朱景宝,宋晋东,李山有.基于深度卷积神经网络的2021年5月21—22日云南漾濞地震和青海玛多地震震级估算[J].地球物理学报,2022,65(2):594-603.
ZHU Jingbao,SONG Jindong,LI Shanyou.Magnitude estimation of Yunnan Yangbi earthquake and Qinghai Madoi earthquake on May 21—22,2021 based on deep convolutional neural network[J].Chinese Journal of Geophysics,2022,65(2):594-603.
[14] ALLEN R M,KANAMORI H.The potential for earthquake early warning in southern California[J].Science,2003,300(5620):786-789.
[15] KANAMORI H.Real-time seismology and earthquake damage mitigation,[J].Earth Planet.Sci.,2005,33,195-214.
[16] WU Y M.KANAMORI H Rapid assessment of damage potential of earthquakes in Taiwan from the beginning of P waves[J].Bulletin of the Seismological Society of America,2005,95(3):1181-1185.
[17] WU Y M,KANAMORI H.Experiment on an onsite early warning method for the Taiwan early warning system[J].Bulletin of the Seismological Society of America,2005,95(1):347-353.
[18] WU Y M,ZHAO L.Magnitude estimation using the first three seconds P-wave amplitude in earthquake early warning[J].Geophysical Research Letters,2006,33(16):L16312.
[19] ZOLLO A,LANCIERI M,NIELSEN S.Earthquake magnitude estimation from peak amplitudes of very early seismic signals on strong motion records[J].Geophysical Research Letters,2006,33(23):L23312.
[20] FESTA G,ZOLLO A,LANCIERI M.Earthquake magnitude estimation from early radiated energy[J].Geophysical Research Letters,2008,35(22):L22307.
[21] WU Y M,KANAMORI H,ALLEN R M,et al.Experiment using the tau-c and Pd method for earthquake early warning in southern California[J].Geophysical Journal International 170,2007,711-717.
[22] BSE M,HAUKSSON E,SOLANKI K,et al.Real-time testing of the on-site warning algorithm in southern California and its performance during the July 29 2008 MW5.4 Chino Hills earthquake[J].Geophysical Research Letters,2009,36(5):L00B03.
[23] HSIAO N C,WU Y M,SHIN T C,et al.Development of earthquake early warning system in Taiwan[J].Geophysical Research Letters,2009,36(5):L00B02.
[24] YIH-MIN W,KANAMORI H,ALLEN R M,et al.Determination of earthquake early warning parameters,τc and Pd,for southern California[J].Geophysical Journal International,2007,170(2):711-717.
[25] CARUSO A,COLOMBELLI S,ELIA L,et al.An on-site alert level early warning system for Italy[J].Journal of Geophysical Research:Solid Earth,2017,122(3):2106-2118.
[26] LIN T L,WU Y M,CHEN D Y.Magnitude estimation using initial P-wave amplitude and its spatial distribution in earthquake early warning in Taiwan[J].Geophysical Research Letters,2011,38(9):L09303,2011GL047461.
[27] ALLEN R M,BROWN H,HELLWEG M,et al.Real-time earthquake detection and hazard assessment by ElarmS across California[J].Geophysical Research Letters,2009,36(5):L00B08.
[28] LIOR I,ZIV A,MADARIAGA R.P-wave attenuation with implications for earthquake early warning[J].Bulletin of the Seismological Society of America,2016,106(1):13-22.
[29] FLEMING K,PICOZZI M,MILKEREIT C,et al.The self-organizing seismic early warning information network[J].Seismological Research Letters,2009,80(5):755-771.
[30] SHIEH J T,WU Y M,ALLEN R M.A comparison of τc and τpmax for magnitude estimation in earthquake early warning[J].Geophysical Research Letters,2008,35(20):L20301.
[31] HEIDARI R,SHOMALI Z H,GHAYAMGHAMIAN M R.Magnitude-scaling relations using period parameters τc and τpmax,for Tehran region,Iran[J].Geophysical Journal International,2013,192(1):275-284.
[32] SASANI M,GHAYAMGHAMIAN M R,ANSARI A.New magnitude scaling relations for earthquake early warning in the Alborz region,Iran[J].Acta Geophysica,2018,66(6):1375-1382.
[33] 周昱辰,黎明,李山有,等.芦山地震序列中地震预警震级估计参数随时间与震级的变化[J].地震工程与工程振动,2018,38(6):64-70.
ZHOU Yuchen,LI Ming,LI Shanyou,et al.Magnitude estimation parameters for earthquake early warning of Lushan earthquake sequence changed in lapse-time and magnitude[J].Earthquake Engineering and Engineering Dynamics,2018,38(6):64-70.
[34] 彭朝勇,杨建思,薛兵,等.基于汶川主震及余震的预警参数与震级相关性研究[J].地球物理学报,2013,56(10):3404-3415.
PENG Chaoyong,YANG Jiansi,XUE Bing,et al.Research on correlation between early-warning parameters and magnitude for the Wenchuan earthquake and its aftershocks[J].Chinese Journal of Geophysics,2013,56(10):3404-3415.
[35] 金星,张红才,李军,等.地震预警震级确定方法研究[J].地震学报,2012,34(5):593-610.
JIN Xing,ZHANG Hongcai,LI Jun,et al.Research on earthquake early warning magnitude estimate[J].Acta Seismologica Sinica,2012,34(5):593-610.
[36] PENG C Y,ZHU X Y,YANG J S,et al.Development of an integrated onsite earthquake early warning system and test deployment in Zhaotong,China[J].Computers & Geosciences,2013,56:170-177.
[37] 李鸿杰,张建经,陈逸民,等.基于2014年云南地区地震的地震预警参数与快速震级估算研究[J].世界地震工程,2018,34(2):123-131.
LI Hongjie,ZHANG Jianjing,CHEN Yimin,et al.Research on earthquake early warning parameters and rapid magnitude estimation based events in Yunnan region in 2014[J].World Earthquake Engineering,2018,34(2):123-131.
[38] 王延伟,李小军,曹振中,等.基于KiK-net井下基岩强震动记录的持续地震预警震级估算方法[J].地震工程与工程振动,2020,40(4):42-52.
WANG Yanwei,LI Xiaojun,CAO Zhenzhong,et al.Continuous estimation magnitude for earthquake early warning based on KiK-net borehole bedrock strong motions[J].Earthquake Engineering and Engineering Dynamics,2020,40(4):42-52.
[39] WURMAN G,ALLEN R M,LOMBARD P.Toward earthquake early warning in northern California[J].Journal of Geophysical Research:Solid Earth,2007,112(B8):1-19.
[40] BROWN H M,ALLEN R M,GRASSO V F.Testing ElarmS in Japan[J].Seismological Research Letters,2009,80(5):727-739.
[41] BHARDWAJ R,KUMAR A,SHARMA M L.Analysis ofTauc (τc ) and Pd attributes for earthquake early warning in India[C]//Proceedings of 15th World Conference on Earthquake Engineering.Lisbon,the Portuguese Republic:[s.n.],2012:126-134.
(本文編辑:贾源源)
基金项目:甘肃省科技重大专项计划(21ZD4FA011);甘肃省自然科学基金(20JR10RA501,23JRRA1399);兰州市科技发展指导性计划项目(2023-ZD-246)
第一作者简介:柴文锐(1996-),男,硕士研究生,主要从事地震预警参数与震级模型研究。E-mail:chaiwenrui@163.com。
通信作者:郭 晓(1974-),男,副研究员,主要从事主动震源技术应用与地震波衰减研究。E-mail:guox@gsdzi.gov.cn。
柴文锐,郭晓,张璇,等.甘肃及邻区基于地震预警参数τc和Pd的震级快速计算模型研究[J].地震工程学报,2024,46(3):703-713.DOI:10.20000/j.1000-0844.20230627001
CHAI Wenrui,GUO Xiao,ZHANG Xuan,et al.Fast magnitude estimation model for Gansu and adjacent regions based on earthquake early warning parameters τc and Pd[J].China Earthquake Engineering Journal,2024,46(3):703-713.DOI:10.20000/j.1000-0844.20230627001

