超临界CO2印刷电路板换热器热工水力特性研究

明杨, 金旸, 杨雯, 赵富龙, 谭思超, 田瑞峰

(1.哈尔滨工程大学 核科学与技术学院, 黑龙江 哈尔滨 150001; 2.中国舰船研究设计中心, 湖北 武汉 430000; 3.中国核动力研究设计院, 四川 成都 610041)

随着能源危机问题的日益突出,核能作为一种稳定、清洁的能源,成为未来发展的主要方向之一。研究人员一直致力于开发核电系统,以满足核电系统高效率和小型化的需求[1]。近50年来,超临界CO2布雷顿循环引起了全世界的广泛关注[2-3]。超临界CO2布雷顿循环系统的热效率高、小型化程度好[4],循环能与出口温度为350～800 ℃的热源较好匹配,适用于诸多第4代核反应堆,具有在能源转换技术领域带来革命性突破的潜力[5]。基本的超临界CO2布雷顿循环由热源、透平、压缩机、换热器等组成,而换热器是超临界CO2布雷顿循环的关键设备。理想的换热器应具有紧凑、传热能力强、压降低等特点,而换热器的性能也与系统的热效率和负荷跟踪特性密切相关[6]。

印刷电路板式换热器(printed circuit heat exchanger,PCHE)被认为是超临界CO2布雷顿循环中换热器的首选[7]。PCHE 是一种紧凑型板翅式换热器,通常采用“化学蚀刻”工艺在传热板表面形成直径为0.5～2 mm的微通道[8],然后将传热板堆叠焊接,形成换热器主体结构[9]。由于PCHE的比表面积大于2 500 m2/m3,在相同的热负荷下,PCHE 的体积约为管壳式换热器的1/5。换热器的冷热侧温差也远小于一般管壳式换热器。因此,PCHE 可以获得较高的传热效率和较小的设备体积,非常适合于超临界CO2布雷顿循环系统[10]。现存的PCHE 按照流动换热方式为横流、平行流和逆流3种;按照流道形状可分为直流道、梯形流道、蛇形流道、正弦流道和锯齿流道5种。

在实验方面,PCHE已被应用于多个小型超临界CO2测试回路,如桑迪亚国家实验室[11]、日本东京科学大学[12]、中国科学院[10]等,学者总结了大量超临界CO2在不同结构流道中流动与传热的经验方程,探讨了入口温度与流速等参数对PCHE传热和效率的影响。在三维仿真方面,对PCHE精细建模的研究大多基于商业计算流体力学(computational fluid dynamics,CFD)软件[13-14]。然而,CFD软件通常使用成本高、计算耗时长,不适于PCHE的瞬态分析和快速设计。因此,简化的一维PCHE 建模方法[15-16]同样受到广泛关注。MA等[17]开发了PCHE动态模型,并通过与超临界CO2系统试验设施的实验数据进行对比验证。JIANG等[18]建立了超临界CO2布雷顿循环的一维模型,发现PCHE对入口温度和流量变化的瞬态响应速度远快于传统的管壳式换热器。XU等[19]建立了PCHE的一维模型,得到了几种不同边界条件下PCHE通道的最优数目。诸多研究结果表明,简化的一维建模方法适用于超临界CO2布雷顿循环PCHE的快速设计和运行特性分析。

本文开发了适用于小型模块化超临界CO2布雷顿循环反应堆系统的PCHE分节点计算程序。采用能量均分法设计PCHE的结构参数,然后基于长度均分法计算了稳态条件下的PCHE热工水力参数分布,并比较了集总参数法和离散建模法在不同节点数下的计算误差,验证了该方法的可行性。

1 印刷电路板换热器的建模与仿真

本文的建模对象为5 MW小型模块化超临界CO2布雷顿循环反应堆系统内的PCHE回热器,其在系统中的布置方式如图1所示[20]。PCHE的热侧入口工质来源于透平,热侧出口连接至冷却器;而冷侧入口工质来源于压缩机,其冷侧出口连接至反应堆。

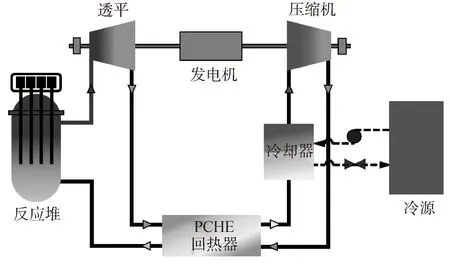
图1 PCHE在系统中的布置方式示意

PCHE的流动布置为逆流,换热通道为半圆形截面的连续直通道。PCHE的三维结构与结构参数如图2所示。

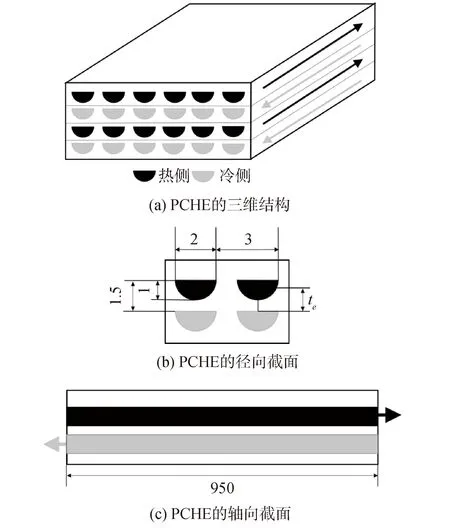
图2 PCHE的结构示意

由于PCHE的通道结构较为复杂,其热工水力特性与传统换热器有明显的不同。并且超临界CO2物理性质会在靠近其拟临界区发生剧烈变化,工质在换热通道内流动过程中的热工水力参数变化不可忽视,集总参数法会带来较大的计算误差。因此,本文采用分节点计算方法,并与集总参数法的计算结果进行了比较。根据超临界CO2布雷顿循环系统内回热器的冷热侧进出口温度、压力、流量与换热功率等参数确定边界条件。基于能量均分法,将PCHE分为若干具有相同热负荷的换热单元,设计其具体的结构参数,完成换热器的初步设计。采用长度均分法,将PCHE分成若干长度相等的换热单元,建立换热器模型的分节点计算模型,主要数学物理方程如下:

根据能量守恒方程,冷热侧节点内流体的能量守恒方程可表示为:

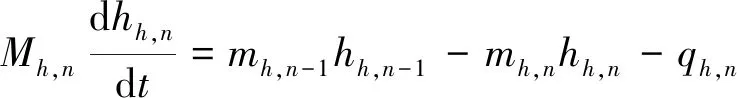
(1)

(2)

式中:mh,n与mc,n分别表示各节点进出口处的流体质量流量;hh,n与hc,n分别表示各节点进出口处流体的比焓;qh,n与qc,n分别表示各节点内由金属壁面传递到冷热侧流体的热量;n个节点长度之和等于PCHE换热通道的总长度。

半圆形流道的水力直径deq及雷诺数Re为:

(3)

Re=ρudeq/μ

(4)

式中:u为节点中的流体流速;ρ为流体密度;μ为动力粘度。超临界CO2半圆形直通道型PCHE的冷热侧努赛尔数与摩擦阻力系数分别为[12]:

热侧:

(5)

冷侧:

(6)

节点冷热侧通道总传热系数U为:

(7)

式中:hh和hc为热侧和冷侧的对流传热系数;te为板厚;kw为PCHE的壁面导热系数。

热侧和冷侧的传热系数为:

hh=Nu·kh/deq,hc=Nu·kc/deq

(8)

式中:kh和kc分别为冷热侧流体的导热系数;deq为通道的水力直径。

考虑到PCHE的半圆形流道结构,换热通道等效板厚te及节点的压降分别为[21]:

(9)

Δpn=2fρu2ln/deq

(10)

式中:f为达西阻力系数;u为流体流速;ln为每个节点的长度。

根据式(1)与(9)求得通道节点内的焓值与压力后,调用物性数据库计算得到节点内的温度:

(11)

冷热通道节点内换热功率qn为:

qn=(Th,n-Tc,n)UnAn

(12)

式中:Un为换热通道节点内的总传热系数;An为节点的总换热面积。

单个通道的总换热量Q和压降ΔP分别为所有节点内的换热功率qn和压降Δpn之和:

Q=q1+q2+…qn-1+qn

(13)

ΔP=Δp1+Δp2+…Δpn-1+Δpn

(14)

PCHE的总换热功率为总传热通道数乘以单通道的换热功率。

2 计算结果分析与讨论

根据超临界CO2布雷顿循环系统主要设备布置,PCHE热侧入口与透平出口相连,边界条件为(714.15 K,8.6 MPa),冷侧入口与压缩机出口相连,边界条件为(352.46 K,15.5 MPa)。根据能量守恒定理和能量均分法设计的PCHE参数如表1所示。

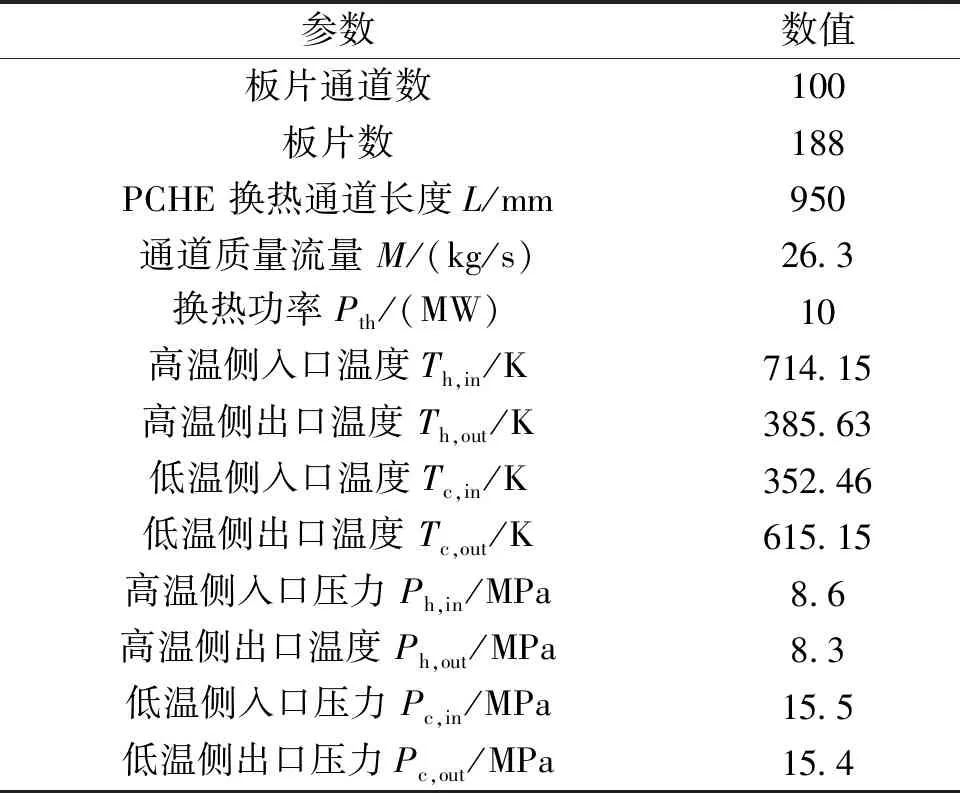
表1 PCHE稳态设计参数

在获得PCHE的设计参数后,根据长度均分法将换热器分成若干节点,然后按照设计参数给出的边界条件进行稳态计算。不同节点数计算结果如表2所示。

表2 不同节点数的计算结果与相对误差

从表2可以看出,随着节点数的增加,计算结果与设计值之间的误差逐渐减小。当节点数为10时,PCHE换热功率Pth的相对误差为11.0%。而随着节点数的增加,误差逐渐减小。当节点数大于等于50时,Pth的相对误差降低至3%。对于PCHE的出口温度,在给定的高低温侧入口温度下,不同节点数的Th,out和Tc,out的相对误差均小于3.2%。当节点数为50时,相对误差减小到0.5%左右。但PCHE的进出口压力对节点数的变化相对不敏感,进出口压力的相对误差几乎保持不变。如表3所示,与集总参数法相比,分节点法的计算精度显著提高。

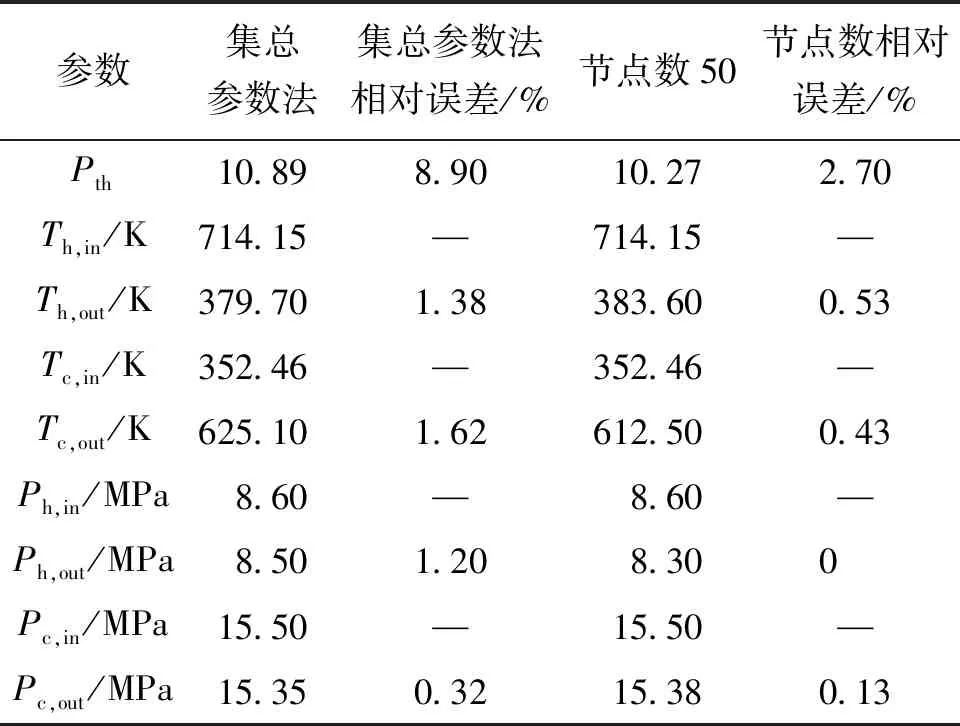
表3 集总参数法与50节点数的计算误差比较

同时,考虑到计算的时间成本,当模拟时间设为1 000 s时,10、20、50、100节点所需的计算时间分别为103、326、959、2 602 s。当节点数小于100时,该计算方法能满足实时仿真的要求(实际计算时间小于等于总仿真时间)。因此,节点数为50的一维离散方法能较好兼顾计算精度和计算成本。

图3和4显示了PCHE热侧和冷侧的温度和压力分布,图5显示了热侧和冷侧节点的温差和传热功率。最大温差出现在PCHE热侧入口段附近,最大温差为108.9 K,换热功率沿热侧流体的流动方向逐渐减小。PCHE换热通道的普朗特数、雷诺数和阻力系数的计算结果如图6所示,热侧和冷侧节点的换系数如图7所示。热侧流体的对流换热系数在入口和出口侧较高,在流道中部较低。此外,由于冷侧流体状态更靠近CO2的拟临界区,其对流换热系数远高于热流体,冷侧流体的对流换热系数沿流动方向由5 298.2 W/(m2·K)降低至3 281.5 W/(m2·K)。换热通道的总传热系数U在1 500 W/(m2·K)。PCHE换热通道整体的热工水力参数与文献[22-23]的计算结果吻合较好。

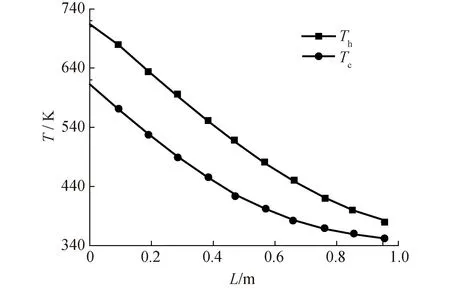
图3 PCHE换热通道的温度分布

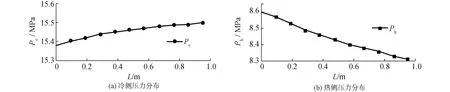
图4 PCHE冷热侧压力分布

图5 PCHE的传热功率分布与温差

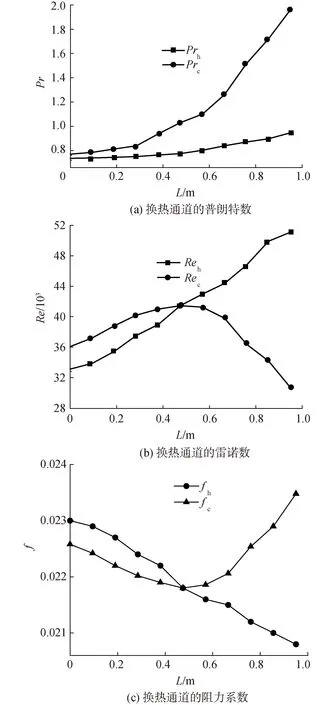
图6 PCHE换热通道内的热工水力参数分布

图7 PCHE的换热系数分布

结果表明,与集总参数法相比,分节点法能更好计算PCHE内热工水力参数沿流动方向上的变化,并能清晰展示换热通道节点内温度、压力、换热功率等主要参数的分布,并且有助于分析换热器内的流动换热过程。此外,由于超临界CO2布雷顿循环的反应堆、压缩机、透平等主要设备对工质温度和压力的变化非常敏感,特别是压缩机的进口参数接近CO2的临界温度和压力,CO2的密度、比热容、热导率等参数会随着温度和压力的变化急剧波动,这将影响整个系统的运行特性。因此,有必要采用分节点法提高PCHE热工水力参数的计算精度。

3 结论

1)计算结果表明,分节点计算方法能较好地显示流体流动方向上温度、压力的变化以及换热通道内的功率分布。

2)超临界CO2在PCHE中的物理性质沿流动方向发生显著变化。采用节点法可显著提高程序的计算精度。

3)考虑到PCHE模型的计算精度和计算速度要求,选取20～50个节点较为合理。

4)研究结果验证了PCHE分节点计算方法的可行性和高精度,为SCO2布雷顿循环系统PCHE的运行特性分析提供了参考,该方法同样适用于 PCHE的快速设计与结构优化。

后续研究将考虑瞬态工况下PCHE的动态参数响应特性,并对算法和模型进行进一步优化。根据超临界CO2布雷顿循环系统其他主要设备的物理模型,建立完整的系统分析程序,研究PCHE与循环中其他主要设备瞬态工况下的耦合影响作用。