波形钢腹板梁T形接头焊接仿真分析与试验研究

冀伟, 张鹏

(1.湖南大学 土木工程学院,湖南 长沙 410082; 2.兰州交通大学 土木工程学院,甘肃 兰州 730070)

波形钢腹板组合箱梁具有自重轻、抗震性能好、跨越能力强、造型美观等优点,在桥梁建设中得到了广泛的应用[1-2]。波形钢腹板与底板通过焊接的方式进行连接,其焊接过程中会产生焊接残余应力和焊接残余变形。焊接残余应力在环境温度和外载荷的作用下容易引起构件发生失稳、甚至断裂失效。因此,研究焊接残余应力和焊接残余变形的对服役期间桥梁的安全评估具有重要研究意义[3]。近年来,国内外学者针对钢结构的焊接已经展开了一系列的研究。于海丰等[4]对小截面焊接工字钢的残余应力进行了试验研究,并分析了板件宽厚比对残余应力的影响;崔闯等[5]采用数值模拟的方法对港珠澳大桥正交异性钢桥面板焊接全过程和残余应力的分布特性进行了研究,发现板厚方向焊接残余应力符合其正弦分布;强伟等[6]通过有限元法研究了铝镁合金T形接头双热源协同焊接温度场、应力场及其变形;Wang等[7]利用切片法和钻孔法研究了高强钢箱梁的残余应力分布规律;耿旭阳等[8]利用有限元软件ProCAST对某跨海大桥钢桥的顶板和U肋间的焊接残余应力进行了研究;刘国宁等[9]利用Simufact Welding有限元软件分析了不同焊接顺序对T型接头焊接温度场、应变场、应力场的影响,得出了不同焊接顺序的优劣排序;唐琪等[10]结合固有相变法和有限元法研究了不同焊接约束对地铁牵引梁焊接变形的影响;胡效东等[11]利用ABAQUS有限元软件对304/Q345R复合板的焊接过程进行了数值模拟,分析焊接过程中复合板的复杂热力学行为。虽然对于各种钢构件焊接的研究较多,但是所研究的构件大都是直线样式的构件,且所研究的都是缩尺比例模型,而通过试验和数值模拟结合研究真实尺寸曲线样式构件焊接少。由于其较复杂的几何构造和独有的“手风琴效应”,波形钢腹板的残余应力分布模式势必与传统直线样式的构件不同;且焊接作业对波形钢腹板弯折角处的应力集中现象的影响也不明确。

本文通过焊接仿真软件Simufact Welding对波形钢腹板T形接头的焊接过程进行模拟,并通过试验来验证数值模拟的正确性,从而得到波形钢腹板T形接头复杂的热力学行为。

1 波形钢腹板梁焊接数学模型

1.1 热传导理论及热源选定

金属材料焊接是一个将局部材料快速加热至高温,随后快速冷却的过程。随着热源的移动,整个焊件的温度随时间和空间急剧变化,材料的热物理性能也随温度剧烈变化,同时还存在熔化和相变时的潜热现象。因此,焊接温度场分析属于典型的非线性瞬态热传导问题[12]。在热分析中,有限元公式的瞬态非线性传热分析控制方程[13]为:

(1)

式中:kx、ky和kz为x、y和z中的导热系数;T为当前温度;Q为发热量;ρ为密度;c为比热容。

焊接温度场和残余应力准确计算的基础为选取合适的热源模型,本文结合焊件的尺寸和焊接的类型选取Goldak所提出的移动双椭球热源模型[14]进行波形钢腹板梁的焊接数值模拟,作用于工件上的体热源沿轴分成前、后2个部分,其几何形状如图1所示,其热源分布函数为:

(2)

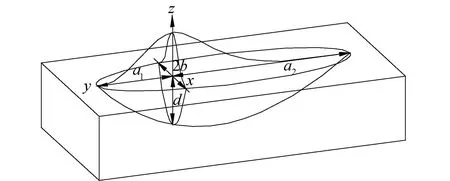
图1 双椭球热源模型

(3)

式中:q0为热量输入值,且q0=ηUI(U为电弧电压;I为电弧电流;η为热效率);f1、f2为热流密度分布系数,f1+f2=2;a1、a2、b、d为热源形状参数,且一般情况下后轴长a2为前轴长a1的2～4倍。

1.2 应力-应变数学模型

采用Von Mises屈服准则、随温度变化的力学性能和线性运动硬化准则,考虑与速率无关的弹塑性本构方程[15],应力应变关系的增量为:

{dσ}=Dd{dε}-CdT

(4)

2 有限元模型的建立

图2为波形钢腹板T形接头具体尺寸图,该型号钢梁由上下底板和波形腹板所组成,每个波段长1 200 mm,为分析研究方便,本文选取一个波段,且不包含上底板的钢梁进行焊接温度场的研究。首先,利用SolidWorks2016软件进行实体模型建立,该模型由腹板和底板构成。然后,在HyperMesh软件中进行实体网格划分,为兼顾计算精度与效率,在焊缝及其附近采用较细密的网格;在远离焊缝的区域,采用较为稀疏的网格,整个模型均采用六面体网格划分,并将网格尺寸设置为10 mm。最后,在焊接仿真软件Simufact Welding中进行焊接参数配置和焊接过程模拟,在此过程为了提高数值计算的精度,在温度场和应力场计算时利用该软件的优势,即网格不需要节点匹配和热源附近网格的自动细化加密功能,对其热源区域的网格进行细化等级为2的加密,故此热源区域网格尺寸为2.5 mm。焊接采用CO2气体保护电弧焊,焊件材料为Q345D,对应软件中的材料S355J2G3,其相关热学参数曲线如图3所示。

图2 焊件尺寸

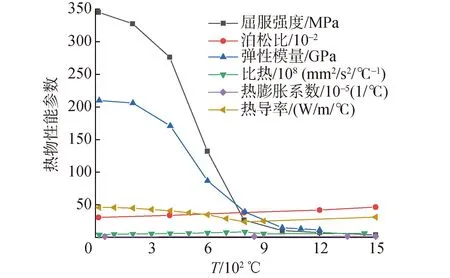
图3 S355J2G3热学参数变化曲线

3 数值模拟结果分析

3.1 温度场分析

Simufact Welding软件的焊接监控器能够对其焊件的焊接情况进行实时监控,对焊接过程中出现的可能导致焊件连接不良的因素进行及时的调整。得到其波形钢腹板梁焊接过程的熔池形貌如图4所示,焊缝的中心温度已经超过材料的熔点1 500 ℃,这说明焊接过程具有足够的能量输入,焊缝金属填料可以全部熔化和焊缝熔深得到保证,波形钢腹板梁的焊接质量高。

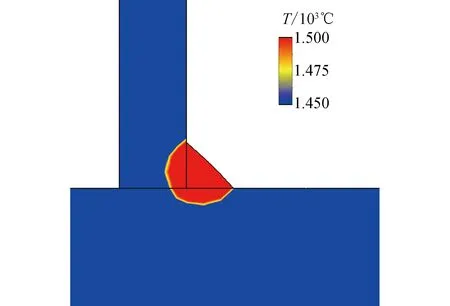
图4 焊接过程熔池形貌及温度场云图

焊接过程中,金属焊缝填料的生成采用生死单元技术来模拟。本文提取波形钢腹板梁在10、270、532和1 500 s时刻的温度场分布云图如图5所示。从图5可以看出,焊件在起弧阶段的温度场是一个瞬态温度场,随着时间的推移,焊接温度场变成了一个准稳态温度场,形状为不规则的椭圆形且熔池温度高达1 684.11 ℃。焊接过程耗时132 s,此后的1 368 s为焊件的冷却阶段。在冷却阶段,由于焊接热源的撤除,焊缝中心及附近的温度快速下降,所表现的温度场呈梯度递减分布,且在波形钢腹板的辐射范围急剧增大。当冷却到1 500 s时,焊件整体温度趋于室温,此时,波形钢腹板梁的整个焊接过程结束。

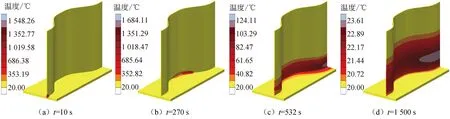
图5 不同时刻试件温度场分布

为了更加直观地描述波形钢腹板梁焊接的温度场分布,沿着焊缝方向在波形钢腹板梁1/2横截面处提取跟踪点的温度历程曲线如图6所示,图中小图表示各温度跟踪点的具体位置。可以看出,波形钢腹板和底板焊趾位置处的跟踪点热循环历程类似,峰值温度都出现在焊缝位置处,且峰值温度都超过了材料的熔点,当离焊缝一定距离后,温度历程曲线趋于重合。距离焊缝越近的跟踪点温度变化越剧烈,而离焊缝越远温度变化则越为缓和,这说明距离焊缝越近热传递越多,温度越高。

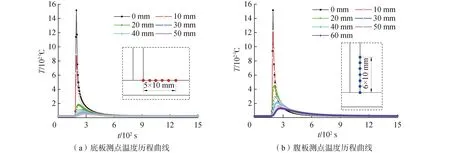
图6 温度历程曲线

为验证数值模拟的可靠性,利用红外测温枪采集波形钢腹板梁焊接过程和冷却阶段温控点的温度。通过Simufact Welding软件自带的测量和数值提取工具提取和试验阶段相同位置的温控点的温度值,将两者进行比较以验证数值模拟的正确性。温控点的具体布置如图7所示,温控点温度对比如图8所示。焊接过程中,温控点温度每5 min中采集一次,冷却过程中30 min采集一次,直至温度冷却至室温,试验结束。在此过程中,为了试验操作的便捷性,仅对1200型波形钢腹板梁的1/2横截面处的测点进行温度值的采集与对比。

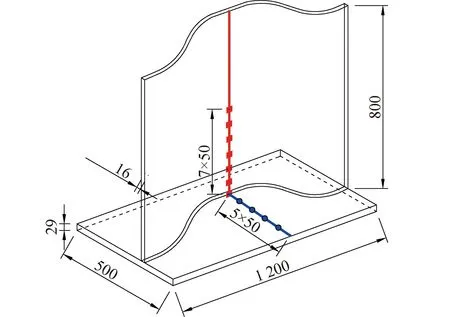
图7 焊接过程温控点布置

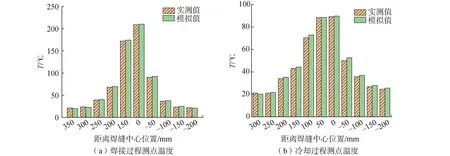
图8 温控点温度对比

从图8焊接过程测点温度对比图可以看出,峰值温度均出现在焊缝位置处,且随着距离焊缝中心位置越远温度值越低。焊接过程中温度测点的温度实测值与模拟值最大相差2.35 ℃,冷却过程测点温度实测值和模拟值最大相差为2.45 ℃,计算2阶段的各点相对误差后发现也都小于5%,故此说明试验所测结果和模拟所得结果吻合良好,证明了数值模拟的正确性。除此之外,还可以看出,焊件温度值的跌幅冷却阶段要缓于其焊接过程,腹板的温度值跌幅大于其底板,这是由于底板的厚度大于波形钢腹板的厚度,热流量腹板大于其底板而导致。热流量的增大会导致焊接变形的产生,为此,在焊接时为防止焊接变形太大而导致构件失稳,要特别注意控制线能量输入的大小。

3.2 应力场分析

焊接材料在焊接过程在焊接过程中会产生材料硬化,如果在计算时不考虑该现象,则可能会使焊接残余应力的结果与实际结果不相符合,从而导致后续结构力学性能分析的结果不合理。为此,本文数值模拟过程中考虑了材料的加工硬化效应[16]。图9为波形钢腹板梁焊接冷却完成之后所得的等效应力云图,从图中可以清楚地看出应力等效应力最大值出现在焊缝中心线上,最大值为370.10 MPa,最小值为0.03 MPa。

图9 等效应力云图

为方便对波形钢腹板梁T型接头的残余应力进行分析,选取了图10所示的2条路径进行研究。图11为波形钢腹板梁焊缝中心线上(路径L1)残余应力的分布曲线。从图11可以发现,残余应力呈峰谷形式分布,纵向残余应力以拉应力为主,最大值371.4 MPa,超过材料屈服强度,这是由于在模拟过程中材料的加工硬化;横向残余应力拉压应力共存,最大拉应力为189.0 MPa,最大压应力为-134.4 MPa。

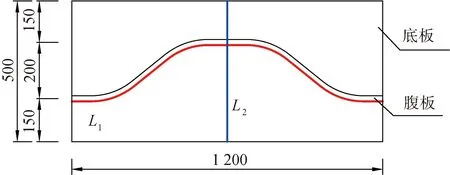
图10 残余应力提取路径

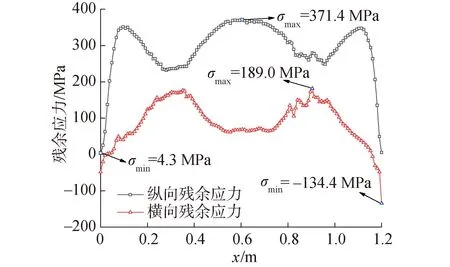
图11 路径L1焊接残余应力分布

除此之外,可以发现,焊件在焊缝的始末两端残余应力发生了大的突变,前者急剧增大,后者急剧减小。这是由于焊件在焊接过程中电弧的引发和收缩引起热源的突然输入和输出所引起。

图12为波形钢腹板梁垂直于焊缝方向(路径L2)残余应力的分布曲线。从图12可以看出,波形钢腹板梁纵向和横向残余应力的峰值均出现在焊缝位置处,纵向残余拉应力最大值为370.5 MPa,超过材料屈服强度,其原为数值模拟过程中考虑了材料的加工硬化;横向残余拉、压应力最大值分别为32.5和-36.4 MPa,而焊缝两端残余应力分布平缓,数值趋近于0 MPa。

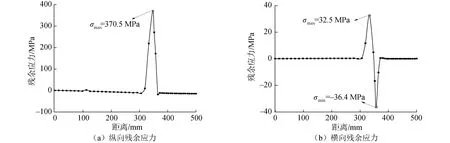
图12 路径L2焊接残余应力分布

为了进一步验证数值模拟的正确性,通过在焊件表面粘贴应变片,利用DH3816N应变测试仪和电脑采集波形钢腹板梁焊接所产生的应变,将计算得出焊接残余应力与数值模拟所得进行比较。

应变花的粘贴位置具体如图13所示。具体表现为:一个波长1 200 mm的波形钢腹板试件从左往右划分为5组标识线,间隔300 mm。考虑到波形钢腹板与底板进行焊接时焊道的温度过高而烧坏应变片,故而从波形钢腹板最低端往上150 mm处开始设置应变片的位置,从150 mm向上每隔50 mm设置一个控制点,每个标示线5个,整个试件共设置25个控制点。底板的控制点从底板与腹板相交到底板边缘每个50 mm设置一个。为了试验过程的简单性,仅将1 200型波形钢腹板梁最中间腹板上的5个残余应力值与数值模拟的应力值进行对比。

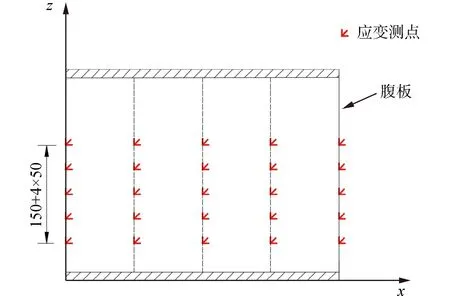
图13 应变花粘贴位置

图14为波形钢腹板梁试验所得残余应力与数值模拟的残余应力的对比图,从图可以看出,波形钢腹板的纵向、横向残余应力的试验值与模拟值之间均有一定的偏差,分析原因是因为焊件在焊接过程中焊缝的温度过高,使得应变花的工作性能下降,从而导致试验结果精度下降。虽然存在一定的误差,但总的来看,波形钢腹板梁的腹板上的残余应力变化趋势大致相同、数值基本吻合,可以证明数值模拟的正确性。

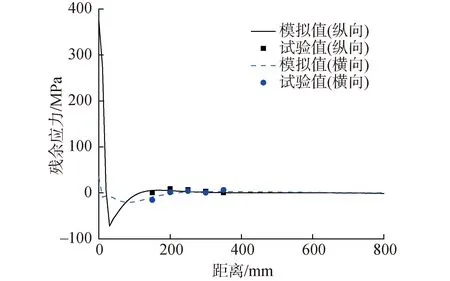
图14 残余应力对比

4 焊速及腹板厚度参数分析

4.1 焊速对残余应力的影响

由于焊接速度会直接影响焊件焊接过程的能量输入,而能量输入的大小则会直接影响焊接温度场和残余应力的分布与大小,本文将利用控制变量法对不同焊接速度下波形钢腹板梁的焊接残余应力进行对比分析。通过3.2节的分析可知,波形钢腹板梁在1/2底板处的焊接残余应力最大,为此,本文针对该部位的残余应力分析研究。在此过程中,焊接速度分别设定为8、10和12 mm/s,其中10 mm/s为试验实测速度。不同焊接速度在波形钢腹板梁1/2底板处的焊接残余应力分布如图15所示。

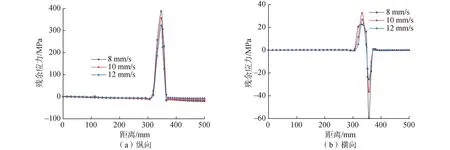
图15 焊接速度对残余应力的影响

从图15可以看出,不同焊接速度所对应的纵向残余应力和横向残余应力的分布规律基本相同,焊接速度所直接影响残余应力的峰值。数值上,当焊接速度从8 mm/s增大到10 mm/s时,纵向和横向残余应力的峰值分别增加了16.7%和56.8%;规律上,残余应力的峰值与焊接速度呈反比关系。除此之外,还可以发现横向残余应力相较于纵向残余应力受焊接速度的影响较大。为此,在保证焊接质量的前提下,应尽可能的提高焊接速度来减小所产生焊接残余应力。

4.2 腹板厚度对残余应力的影响

为了研究腹板厚度对波形钢腹板梁焊接残余应力影响,利用Simufact Welding软件分别对腹板厚度为16、18和20 mm的波形钢腹板梁进行了焊接模拟,得到了波形钢腹板梁1/2底板处的焊接残余应力分布如图16所示。其中16 mm为试验梁的实测数据,且除腹板的厚度以外,其余各尺寸、参数均相同。

图16 底板厚度对残余应力的影响

从图16可以看出,焊件1/2底板处纵向残余应力随着波形钢腹板厚度的增加残余应力峰值有明显地减小,但其总的分布规律基本相同;从图16(b)可以看出,随着腹板厚度的增加焊件的横向残余应力峰值大小的变化与其纵向残余应力一致,但应力的分布规律发生了大的变化。在焊缝附近,腹板厚16 mm的焊件横向残余应力状态为拉-压,而腹板为18和20 mm时所得的残余应力状态为拉-压-拉。而远离焊缝的部位,残余应力几乎不受腹板厚度的影响。为此,在工程实际中,为了使波形钢腹板梁的焊接残余应力变小和受力状态更合理,应尽可能的增大腹板的厚度。

5 结论

1)波形钢腹板梁在焊接过程中,焊缝区域距离熔池中心越近,焊接温度场变化越快,温度也越高,焊缝任意位置总的温度变化规律基本一致,所得焊接热影响区分布为不规则的封闭椭圆形。焊后冷却时,焊缝区域温度迅速降低,温度场范围分布越来越大。

2)不论垂直还是平行于焊缝的残余应力均以纵向残余拉应力为主,残余应力离焊缝越近数值越大,最大值均出现在焊缝的中部,且都超过了材料的屈服强度。横向残余应力的应力水平相对较低,拉压应力共存,离焊缝位置越远,应力变化越稳定。

3)波形钢腹板梁焊接残余应力的分布规律几乎不受焊接速度的影响,但残余应力的峰值受焊接速度影响较大。因此,在保证焊接质量的前提下,应尽可能的提高焊接速度来减小所产生焊接残余应力。

4)波形钢腹板梁残余应力的峰值随底板厚度的增加而减小,其纵向残余应力分布规律不受底板厚度的影响,横向残余应力则反之。在工程实际中,为了使波形钢腹板梁的焊接残余应力变小和受力状态更合理,应适当的增大腹板的厚度。