广义频分复用系统峰均功率比抑制算法

宁晓燕, 刘承赟, 谌星宇, 王震铎

(哈尔滨工程大学 信息与通信工程学院,黑龙江 哈尔滨 150001)

广义频分复用(generalized frequency division multiplexing, GFDM)作为广义的多载波技术,将调制数据划分为多个子载波与多个子符号,将不同子符号上的全部载波以不同的滤波器进行调制[1]。通过调整子载波与子符号的数量GFDM系统可退化为正交频分复用系统(orthogonal frequency division multiplexing, OFDM)或者单载波系统,选择不同的成型滤波器也可得不同的性能[2]。相较于OFDM,GFDM系统具有良好的灵活性与更好的带外性能。高峰均功率比(peak to average power ratio, PAPR)的信号通过高功率放大器会使设备饱和,导致带外泄露,从而增加符号的错误率。因此多载波系统在实际应用中都需要考虑降低PAPR。在传统OFDM系统中降低PAPR的方法可大致分为3类:预畸变类、编码类和概率类。预畸变类中具有代表性的方法为限幅法[3],限幅法是牺牲误码率及带外性能换来了较好的PAPR性能。概率类方法是牺牲复杂度来获得PAPR性能的提升,其PAPR抑制效果略差于限幅法,但其误码率和带外性能不会发生改变[4],而预编码类则需要对信息进行预处理,会增加系统复杂度,且预编码类技术对PAPR的抑制性能有限,因此其只适用于一些特定的场合[5-6]。在GFDM系统中可以通过调节系统参数降低系统PAPR,如子载波数,时隙数与成型滤波器的滚降因子[7-8]。但是这些系统参数的改变会连带影响系统,如带外、复杂度、误码率等其他性能。近年来,学者根据前述OFDM系统中降低PAPR的方法,提出了降低GFDM系统的PAPR算法[9-14]。其中限幅法是最有代表性的一类方法,但是会使得系统的带外性能及误码性能下降,而GFDM系统是通过牺牲系统误码率换来了带外性能的提升,因此传统限幅法并不适用于GFDM系统。

本文通过选取部分子载波来对传输信息的PAPR进行抑制,基于限幅法的原理,提出了一种适用于广义频分复用系统的子载波抑制高峰均功率比(peak to average power ratio reduction sub-carriers, PRSC)算法,利用迭代限幅来确定抑制PAPR的子载波上的数据。与限幅法相比,以降低系统信息传输效率为代价,在不改变系统的带外性能与高白噪声下的误码率性能的情况,获得较好的PAPR抑制效果。

1 广义频分复用系统模型

GFDM系统是一种基于数据块的滤波器多载波调制系统[2]。GFDM调制后的离散信号为:

n∈{0,1,…,N-1}

(1)

式中:x(n)为信息的第n个采样值;dk,m为调制到第k个子载波与第m个子符号上的原始数据;N为总采样点数;K和M分别为总子载波数与总时隙数;gTX(n)为N的滤波器,通常使用升余弦滤波器。

假设系统经过加性高斯白噪声(additive white gaussian noise,AWGN),则接收到的信号为:

y(n)=x(n)+w(n)

(2)

n∈{0,1,…,N-1}

(3)

式中gRX为解调滤波器,而根据gRX的不同,接收机可分为3种分别为:匹配接收机、迫零接收机以及最小均方误差接收机。GFDM信号的PAPR为:

(4)

GFDM系统是以数据块的形式进行数据传输,相干的子载波与重叠的子符号都会导致GFDM系统的PAPR升高。其PAPR的理论上限为[15]:

(5)

因此GFDM系统与OFDM系统都具有高峰均功率比的问题。

2 基于子载波抑制峰均功率比的算法

本文借鉴限幅法的思路[16],提出了采用迭代限幅方式的PRSC算法来降低GFDM系统的PAPR。与直接限幅法相比,PRSC算法能降低系统的PAPR,且几乎不会影响带外及误码率性能,但其计算复杂度较限幅法更高且抑制PAPR的效果也不如限幅法。因此本文进一步提出将PTS与PRSC相结合来进一步抑制系统的PAPR。

2.1 基于PRSC算法的PAPR抑制方案

PRSC算法是在进行GFDM调制的子载波中选择部分子载波来传输用于抑制其余传输数据子载波产生的高PAPR数据的方法,其具体流程如图1所示。假设GFDM系统的子载波数为K,其中用于传输信息的子载波数为I,而抑制PAPR的子载波数为D,因此K=I+D。

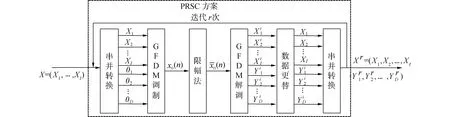
图1 PRSC算法流程

1)将初始信息进行GFDM调制得到时域信号,即x=A·X,其中A为GFDM调制矩阵,调制信息X为:

(6)

2)将得到的时域信号x0(n)按照限幅法来抑制PAPR,其中限幅阈值为Amax,则限幅后的信号为:

(7)

而阈值Amax由限幅率(clipping ratio, CR)产生,Amax=σ×10(ACR/20),其中σ为信号功率的均方根。

(8)

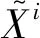
本文提出的PRSC算法的复杂度与迭代次数r成正比,采用Gabor变换进行简化的GFDM系统的调制与解调的复杂度都是MKlbK+M2K/2[17],因此PRSC方案的复杂度为2×r×(MKlbK+M2K/2)。而穷举法的复杂度则取决于初始序列的调制阶数以及PAPR抑制载波D的数量。随着该参数的增加复杂度呈指数上升,迭代限幅法的复杂度较穷举法更低。在接收端只需要对GFDM解调后的信息进行抽样,只抽取非抑制载波中的信息就能得到最终数据,所以PRSC算法在接收端的实现复杂度低,且不会对误码率性能造成影响。由于在限幅后使用了初始信息替换限幅后的信息,这会使得PAPR再次升高,所以PRSC算法的PAPR抑制效果略差于限幅法。因此本文又提出将概率类中的PTS算法与PRSC算法结合来进一步降低系统PAPR的算法。

2.2 基于PRSC-PTS算法的PAPR抑制方案

PRSC算法能对时域信号的峰值功率进行压缩,PTS算法则是对不同类的子载波加入不同的相移,从而降低产生过高峰值功率的可能性,因此可将PTS方案与PRSC结合来进一步抑制GFDM系统的PAPR。若先进行PTS再进行PRSC需要多进行一次GFDM调制,因此先进行PRSC再进行PTS可以省去一次GFDM调制。其具体流程如图2所示。

图2 GFDM系统PRSC-PTS算法总体结构

先将初始信息进行PRSC调制得到时频信号X(r),把信号按照子载波分为V组,每组不同子载波之间互不重叠,互不重叠的部分进行补0:

(9)

对V个互不重叠的子载波乘以不同的相位,可得:

(10)

最终比较不同相位下的PAPR值,选取最佳相位进行最终的数据传输。在接收端对接收信号解调后进行相位补偿,消除PTS算法中相位变化的影响,再进行数据抽样得到最终信息。因此PRSC-PTS算法也不会对误码率性能造成影响,且其PAPR性能相较于PRSC算法得到了进一步的提升。

3 抑制算法仿真分析

3.1 PRSC算法参数影响分析

本文对所提出的应用于GFDM系统中的PRSC方法进行仿真分析,在该技术中,影响PAPR性能的2个主要参数为迭代次数及PAPR抑制载波的分布。其具体的仿真参数如表1所示。

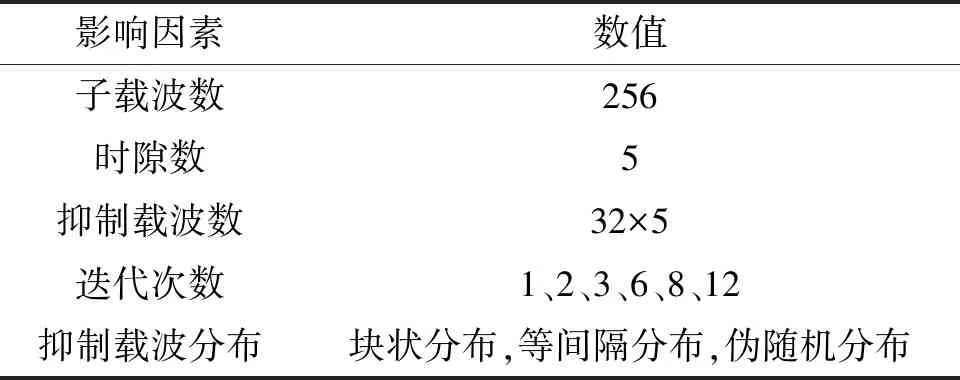
表1 PRSC算法仿真参数

图3给出了不同PAPR抑制载波位置情况下的仿真对比分析,其中迭代次数固定为8。经过PRSC处理后的GFDM系统的PAPR结果比GFDM本身更好。对比3种载波位置的分布可以看出,采用伪随机分布确定抑制载波位置的PAPR抑制效果最好,等间隔分布的PAPR抑制效果次之,而块状末尾分布的效果最差。以PAPR值为10-3作为标准,相较于GFDM系统本身,末尾块分布有0.4 dB的增益,等间隔分布有1 dB的增益,伪随机分布有1.3 dB的增益。因此以伪随机序列来确定载波位置。

图3 PRSC算法在不同载波位置下的对比

图4给出了不同迭代次数下的PAPR性能,其中PAPR抑制载波位置的分布是采用伪随机序列确定。从仿真结果上来看,随着迭代次数的增加,系统的PAPR性能逐渐下降,其中迭代次数为1、2、3时,能看出来系统的性能明显下降,而随着迭代次数的增加,系统的PAPR抑制效果降低。

图4 PRSC算法在不同迭代次数下的对比

为比较迭代次数对系统PAPR性能的影响,图5给出了门限PAPR界限为9,PRSC算法在GFDM系统处于不同参数下的收敛性对比,其中子载波数K取128、256、512;时隙M取3、5、7;成形滤波器阶次a取0.3、0.7。由仿真结果可知,随着K与M的增加,系统PAPR值也会升高。当迭代次数在5以内时,随着迭代次数的增加,PAPR性能提升明显,当迭代次数在5～10时,PAPR性能提升变缓,而当迭代次数大于10时,PAPR性能慢慢收敛。结合图4与图5,当迭代次数超过6时,其性能降低的程度会越来越少,且与复杂度不成正比。

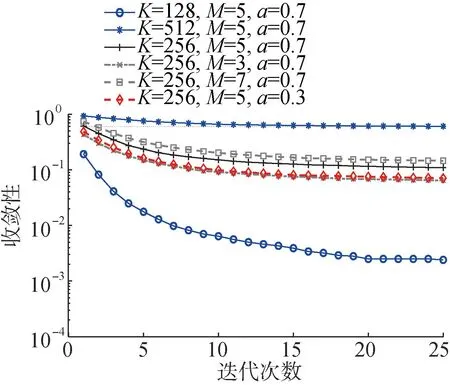
图5 PRSC算法在GFDM不同参数下的收敛性

3.2 PRSC算法,PRSC-PTS算法与限幅法性能对比

对3种PAPR抑制算法从PAPR,带外和误码率3种方面进行讨论。其中GFDM系统的子载波数为256,子符号数为5,限幅率为0.1,PRSC技术的迭代次数为6,PAPR抑制载波数为32×5,且抑制载波位置由伪随机序列来确定,PTS分组将子载波分为4组,32组随机相位。

图6中给出了中心频率为100 MHz,子带带宽为15 kHz情况下,本文提出的PRSC算法和PRSC-PTS算法与直接限幅法的带外性能对比。可以看出直接限幅法带外泄露较高,而本文提出的PRSC法与PRSC-PTS法几乎不会对带外性能造成影响。这是因为直接限幅法使时域信号产生了非连续变化,从而导致带外泄露高。PRSC算法则是对时域信号的峰值功率进行了压缩,并没有非连续点。PTS算法则是引入了相位,也不会产生非连续点,因此2种算法几乎不会对系统带外性能产生影响。

图6 GFDM在3种算法下的带外性能

图7中给出了本文提出的PRSC算法和PRSC-PTS算法与直接限幅法的误码率性能对比。可以看出,直接限幅法会降低系统误码率性能,而PRSC法与PRSC-PTS法则不会对系统的误码率性能造成影响。直接限幅法由于在发射端对信号进行了不可逆的变化,因此其误码率性能会随着限幅率的提升而不断变差。PRSC算法在对调制信息进行正常解调后,直接去掉抑制载波位置处的信息得到最终结果,因此几乎不会对误码率性能造成影响。PRSC-PTS算法则是在PRSC的基础上加入了不同的相位,消除相位影响之后也几乎不会对系统性能造成影响。

图7 GFDM在3种算法下的BER性能

图8中给出了本文提出的PRSC算法和PRSC-PTS算法与直接限幅法的PAPR性能对比。3种算法的PAPR性能均比GFDM系统本身的PAPR好,在10-3情况下,相较于GFDM系统本身,PRSC算法有1 dB的增益,直接限幅法有2.8 dB的增益,而PRSC-PTS算法则有3.3 dB的增益。可见PRSC-PTS技术通过引入对多种相位的选择,降低了出现较高瞬时功率的可能性,在不影响PRSC技术的带外与误码率的前提下,取得了更好的PAPR抑制效果。

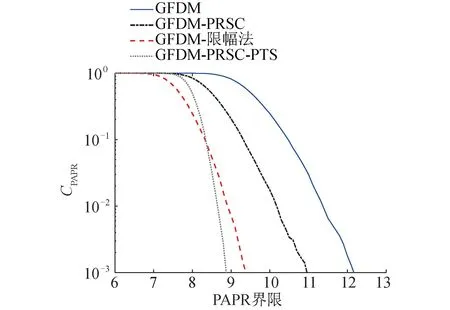
图8 GFDM在3种算法下的PAPR性能

4 结论

1)PRSC算法几乎不会对GFDM系统的带外及误码率性能产生影响,PAPR在10-3的情况下,采用PRSC算法的PAPR值较GFDM本身有1 dB左右的增益,直接限幅法则有2.8 dB左右的增益。

2)本文算法的PAPR值有3.3 dB的增益,PAPR抑制性能与限幅法相同,且不会对系统带外及误码率性能造成影响。

发射端需要对传输的信息进行处理,复杂度较高。在未来的工作中,将致力于研究更适用于GFDM系统的复杂度较低的PAPR抑制算法。