基于多层优选卷积的水声信号样本自动标注方法

王红滨, 张帅, 何鸣, 陈夏可

(1.哈尔滨工程大学 计算机科学与技术学院,黑龙江 哈尔滨 150001; 2.黑龙江科技大学 计算机科学与信息工程学院,黑龙江 哈尔滨 150022)

水下声信号标注的发展缓慢,导致水声信号的模式识别任务面临水下声信号数据集少,数据集的数据量不够大以及数据集不够准确的现状。并且由这些数据集训练出的模型泛化能力较低,对细微的噪声和干扰敏感,不能正确进行模式识别。传统的标注方法通过人工对声音信号进行标注,不仅费时费力,经济效益也不高,同时受标注人员专业性的限制,其标注的准确性往往也不能达到要求。

声纹识别技术[1-3]通过对一种或多种声音信号的特征进行分析,可辨别声音信号,判断某一个声音信号是否由某物或者某人发出。在声纹识别领域,一般通过声学模型提取出声纹的声学特征,再根据得到的声学特征采用识别算法,对声音进行识别分类、标注。一般常用的声纹特征为线性预测倒谱系数(linear prediction cepstral coefficients,LPCC)[4-5]、梅尔频率倒谱系数(Mel Frequency cepstrum coefficient,MFCC)[6-7]等。

传统的识别技术一般基于统计模型,例如隐马尔可夫模型(Hidden Markov model,HMM)[8],高斯混合模型(Gaussian mixture model,GMM)[8],高斯混合模型-通用背景模型(Gaussian mixture model-universal background model,GMM-UBM)[9]等,属于早期常用的声纹识别方法。这些方法模型在现在的部分场景中虽然还可以继续使用,但是它们使用场景过于单一、使用范围小,不能使用在一些场景复杂的应用中,而现在的声纹识别多要求应用于复杂的场景中[10]。因此,众多的深度学习方法被应用到声纹的模式识别任务中。基于卷积神经网络(convolutional neural networks, CNN)[11]、循环神经网络(recurrent neural network, RNN)[12]等多种神经网络的各种声纹识别系统层出不穷。其中有百度提出的一种端到端的Deep Speaker[13-15],谷歌推出的Google Cloud 声纹识别平台。同时,在国际声纹识别比赛中,各种基于深度学习的声纹识别模型屡次刷新最好成绩,目前单网络模型中识别率最好的是ECAPA-TDNN[16]模型,该模型是一种基于CNN进行改进的模型。同时,还有将不同的网络模进行融合,例如将CNN和RNN相结合的RBFNN-CNN[17]。

本文使用声纹识别技术[1]进行水下声信号数据自动标注,利用传统的声学模型计算出水下声信号的声学特征。针对水声信号自动标注任务,基于深度学习的方法,提出了多层优选卷积(multilayer optimal convolution, MOC),并进行水声信号特征嵌入的提取,完成分类及标注。

1 基于优选卷积的多层优选卷积模型

1.1 优选卷积的OCA-Block

SE-Block通过使用挤压[18]与激励操作[19]得到不同通道的权重,模型可自主判定哪些特征嵌入的重要性。但却有可能导致部分重要的特征嵌入丢失,从而降低了模型的性能[20]。为了减少该操作带来的特征嵌入的损失,本文使用1个一维卷积层取代SE-Block中的第1个全连接层,减少了使用全连接层带来巨大的参数量。本文通过使用卷积层,可有效地减少参数计算量,提升了模型的计算速度,减少运算时间。相较于全连接层,使用一维卷积层能够捕捉到输入更多的低级特征,更深层的卷积层可以基于此进一步提取更高级语义特征,因而能够大大减少特征嵌入损失。

本文在一维卷积层后引入优选卷积层(optimal convolution layer,OC-Layer),OC-Layer利用优选算法找出每层中最合适的卷积核,通过优选卷积操作能够在声学信号特征中进行小范围内跨信道交互,以便获取更优、更具有代表性的特征嵌入。考虑到不同的OC-Layer操作之后得到的特征信息不同,因此采用多层特征融合思想,将多层OC-Layer的输出进行聚合。

基于以上想法,本文提出了一种优选卷积层注意力机制(optimal convolution attention mechanism,OCA),本文称为OCA-Block,本文采用一维优选卷积层即为OC1d-Layer。模块结构如图1所示,k为卷积核大小,n为奇数,表示在优选层中有k= (1,3,…,n)的卷积核。

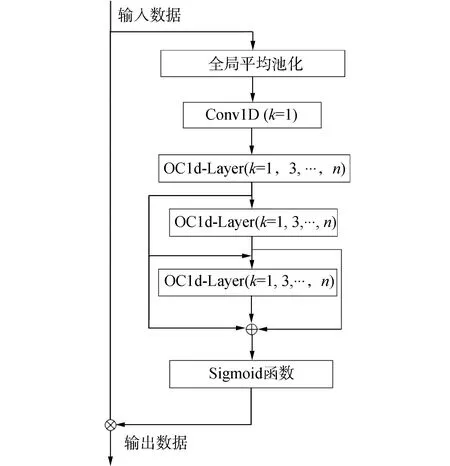
注:Conv1D为一维卷积

1.2 使用优选算法的OC1d-Layer

本文在每个OC1d-Layer中设置了多个大小不同的卷积核。卷积核尺寸与处理过的声学模型有关,利用其信号的声学特征维度设置卷积层的最大核尺寸。本文数据集中的声学特征为梅尔频谱,频域维度尺寸为80维,k=7时最大的卷积核尺寸为:

k=lbc

(1)

式中:c为声学特征的频域维度的大小;k为卷积核尺寸,向上取整,若k为偶数,则k+1。

本文对更大尺寸的卷积核也进行了研究。在每个OC1d-Layer中都有(n+1)/2个卷积核即(1,3,…,n)。针对这些不同尺寸的卷积核,本文使用相似度方法计算每2个不同卷积核运算出来的输出,找出相似度最优的2个卷积核,取卷积核尺寸大的作为该层的卷积核。因为2个不同尺寸的卷积核,大的卷积核卷积后产生的数据参数较少。后面的OC1d-Layer以此类推。本文使用了余弦相似度、汉明距离、斯皮尔曼相关系数[21-23]这3个相似度算法进行实验研究。

针对OCA-Block,考虑到OC1d-Layer作为整个模型中的子模块,层数不宜过深,经过实验验证,3层是比较合理的设置。

1.3 优化运算时间的OCA-Res2Block

本文通过将注意力机制以及残差思想[24-26]进行结合,提出了如图2所示的优选卷积残差模块,称为OCA-Res2Block。在该模块中首先使用了一个Res2Block模块,然后在该模块后面接入一个基于注意力的OCA-Block。简单地增加模块数量并不一定能够对模型的性能产生积极影响,反而可能会降低模型的运行效率。本文进一步研究了OCA-Res2Block模块的个数,并展开了一系列探索性实验。

注:1.Conv1D为一维卷积,2.BN为批处理归一化,3.ReLU为激活函数。

1.4 基于优选卷积的MOC

本文中对多种声纹识别系统[27-28]进行了研究,并提出了图3所示的MOC,将多层特征融合和注意力机制结合。

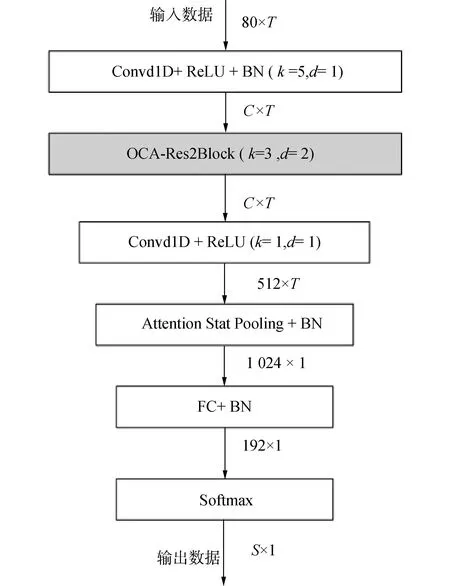
注:1.C、T分别为输入的大小,2.k为卷积核大小,3.d为空洞卷积的膨胀率,4.S为类别数,5.FC为全连接层

2 实验结果与分析

2.1 数据集与实验设备

本文中采取浙江省德清县对河口水库音频作为的数据集。为了保证数据集具有普遍性,该数据集考虑到了时间、温度、天气、距离、深度、频率等多种环境因素。整个数据集包含3个时间段(上午、中午、下午);5种深度(1、3、5、7、9 m);2种频率(单频CW、调频LFM);2种距离(75、150 m)即声源到声音接收器的距离;32个通道;每种音频数据录制90 s。本文从整个数据集中抽取2组数据,同时为了便于实验将90 s的完整数据切分为900份0.1 s的片段,即2组数据包含75 MB、150 MB的CW、LFM,同时每组数据有32个通道。由于使用设备的原因在进行梅尔特征提取时,采样率设置为1 000 000。在实验数据集中,本文将数据集设置为训练集与测试集2种,所占比例为80%:20%。

2.2 实验评估指标

在实验中,本文将标注准确率作为评价指标。标注准确率为在标注任务过程之中,标注正确的样本占总测试样本的比值:

Acc=∑St/L(S)

(2)

式中:St为在数据集S中标注为t,即标注正确的数据个数;L(S)为数据集S的总样本数。

2.3 结果及分析

本文中将正常水声信号和其中的噪音进行分类标注。为从不同角度探索模型优化的可能性,进行了4种类型的实验。分别关注于简化OCA-Res2Block模块数量以实现时间优化、OC1d-Layer的层数、OC1d-Layer中卷积核的选择,以及不同卷积核相似度计算方法。每种类型的实验都包括了多个实验组。作为参照,本文选用了当前单网络模型中识别率最高的ECAPA-TDNN作为基线模型。在MOC的默认设置中,配置了一个OCA-Block,OC1d-Layer的层数为3,OC1d-Layer中的卷积核尺寸设置为K=7,即每个OC1d-Layer包含1、3、5、7共4种尺寸的卷积核,相似度计算采用斯皮尔曼相关系数。

2.3.1 OCA-Res2Block的时间优化实验

本文以运行时间及数据标注的准确率作为评判指标,采用MOC,分别设置一个OCA-Res2Block、2个OCA-Res2Block,标记为F1、F2,除了OCA-Res2Block个数,其他参数为默认设置参数,包括OC1d-Layer的层数设置为3,OC1d-Layer中的卷积核尺寸设置为K=7。实验时间优化实验结果如表1所示。

表1 OCA-Res2Block时间优化实验结果表

由表1可得,F1模型的运算时间远低于F2模型和基线模型,运算时间分别优化了55.4%、43.5%,但是F1在准确率方面与F2模型最高的准确率持平、比基线模型最多高出1.17%。同时可以发现F2模型的运算时间比基线模型高出21.1%,但是其准确率要高于基线模型。由此说明使用F1模型即本文提出的OCA-Res2Block模块的使用注意力机制和优选算法是有效的,以及适当的减少模型模块的构成能够减轻模型的计算压力和运行时间。同时可以看到在这2组数据中提出的MOC模型比基线模型从运行时间和准确率2个方面都有较大提升,即MOC全面优于基线模型。

2.3.2 OCA-Block中OC1d-Layer层数设置实验

在该类实验中,本文用数据标注的准确率作为评判指标,在实验过程中,本文将OC1d-Layer层数分别设置为3、5、7层标记为O3,O5,O7,除了OC1d-Layer层数,其他参数为默认设置参数,包括OC1d-Layer的层数设置为3,OC1d-Layer中的卷积核尺寸设置为K=7。实验结果如表2所示。

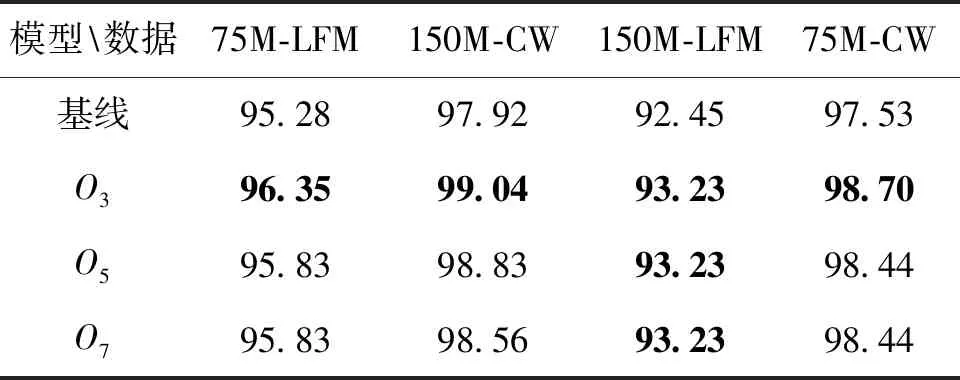
表2 OC1d-Layer层数实验结果表

由以上结果可分析出:在MOC中将优选卷积层的层数设置为3层时,在距离为75 M时CW与LFM中最大的准确率分别为96.35%以及99.04%;在距离为150 M时CW与LFM中最大的准确率分别为93.23%及98.70%。说明本文中提出3层OC1d-Layer有效,随意加深层数对模型并无益处。因为并行的逻辑层只增加收敛速度,而本模型并没有随便增加层数。并且过多的层数可能会导致模型本身更加复杂,如果训练数据本就不多,很容易造成过拟合的问题。通过实验结果可以发现无论几层OC1d-Layer的MOC的准确率都比基线模型的准确率更高,即说明MOC优于基线模型的。

该类实验说明本文中提出的OC1d-Layer有效,并且从实验的结果可以推测出层数的阈值为3。

2.3.3 OC1d-Layer中优选算法的对比实验

在该类实验中,本文用数据标注的准确率作为评判指标,并验证优选算法的有效性以及最佳的卷积核尺寸。在实验过程中,除了卷积核尺寸和个数,其他参数为默认设置参数,包括OC1d-Layer的层数设置为3,OC1d-Layer中的卷积核尺寸设置为K=7。在实验中,本文设置OC1d-Layer中的卷积核尺寸以及卷积核数如表3所示。

表3 卷积核尺寸以及卷积核数表

优选算法实验结果如表4所示。

表4 优选算法实验结果表

由以上结果可得,将OC1d-Layer中的最大卷积核尺寸设置为7,在这2组数据中标注准确率均达到最优,K7模型优于基线模型,本文提出的优选算法有效。同时,也可以发现在75 M的CW数据中,K5、K11的标注准确率低于基线模型的标注准确率,说明了本文中设置的K7是当前最优的,也证明了在OC1d-Layer中设置卷积核尺寸以及个数应该按照声学模型产生的声信号特征进行设置。

2.3.4 OC1d-Layer中相似度算法的对比实验

该类实验主要将3种相似度算法进行研究。本文用数据标注的准确率作为评判指标,在实验过程中,采用的相似度函数分别为余弦相似度、汉明距离、斯皮尔曼相关系数标记为Mc、Mh、Ms,除了相似度算法,其他参数为默认设置参数,包括OC1d-Layer的层数设置为3,OC1d-Layer中的卷积核尺寸设置为K=7。相似度算法实验结果如表5所示。

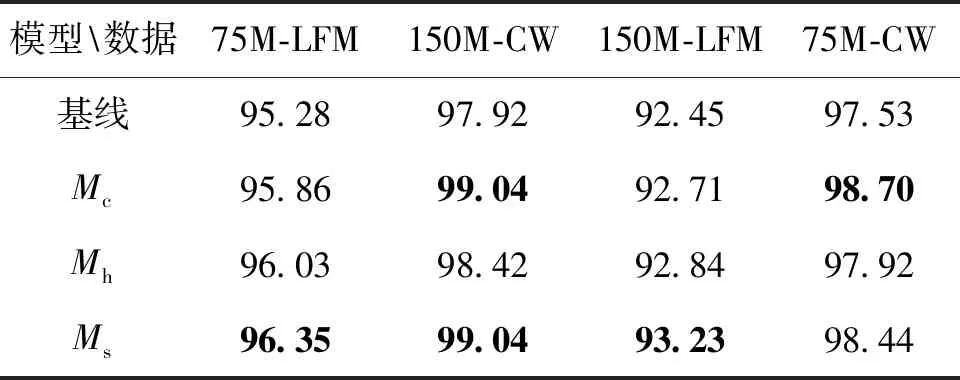
表5 相似度算法实验结果表

由以上结果可分析出,在75 M的LFM数据中,余弦相似度与斯皮尔曼相关系数算法准确率为99.04%;75 M的CW数据中,斯皮尔曼相关系数算法准确率为96.35%。而在150 M的CW数据中,斯皮尔曼相关系数算法准确率为93.23%;在150 M的LFM数据中,余弦相似度算法准确率为98.70%。在OC1d-Layer中使用不同的相似度算法得到的准确率不同,但在相同的数据集中,准确率的差别不到1%。从整体来说,在这3种算法中,斯皮尔曼相关系数算法较为合适。本文使用斯皮尔曼相关系数算法作为相似度算法合理。在模型中无论使用哪种算法,其标注准确率都高于基线模型。

3 结论

1)本文使用优选、注意力机制、多层特征融合等策略,实现了MOC在运算时间和标注准确率方面的预期目标。

2)本文MOC在河口水库采集的音频数据集上取得了的标注准确率为99.04%,高于基线模型的97.92%;同时运行时间较少了43.5%。本文提出的方法使用时间更短,并且对水声数据的标注准确率更高。

3)相同环境下,LFM波形数据的标注准确率高于CW波形数据。该模型的使用提高了水声信号标注的准确率和效率。

在以后研究中,将进一步研究MOC的改进,同时考虑将2个网络模型并行使用的研究,进一步提高水下声信号自动标注的标注性能。