控制工程中MATLAB 的时域分析与根轨迹绘制应用探究
吴 理, 李自成,2, 罗敬崴, 刘曾杉, 申启俊
(1.成都理工大学工程技术学院, 四川 乐山 614000; 2.核工业西南物理研究院, 四川 成都 610000)
0 引言
时域分析法利用对系统的微分方程式及时间传递函数,进行拉普拉斯转换求得系统实际输出的表达式。根据给出的信息可以计算得出控制器的时间响应,然后再利用响应图来解析控制器的特性。但是在这中间的处理过程中需要较大的运算量,而且既耗时又费脑。根轨迹分析法理解控制系统的图解方法更加便捷,于是就需要利用MATLAB 软件分析控制的性能指标,并通过绘制系统的阶跃信号响应曲线图与根轨迹简洁直观的显示出来。使用SimuLink 对系统进行建模与仿真避免在实际工程应用中产生问题。
1 线性定常系统的时域响应
线性系统的时域分析法在自动控制系统中,对于线性定常控制系统,根据系统的运动规律与特点,可利用时域分析法去分析控制系统的性能。通过微分方程便可以求出系统的动态性能指标。
数学模型对任何系统进行分析都需要先进行建立,系统数学模型是针对各变量间相互作用和变化规律的数学描述。在自动控制系统中,建立这种模型是系统分析的基础。MATLAB 提供了多种工具和函数,用于创建控制系统的数学模型,包括传递函数、零极点增益和状态空间模型。这些模型有助于理解系统特性,选择合适的控制策略,并优化系统性能。
本文只对传递函数模型进行研究,某输入输出分别用U(t)、Y(t)来表示,并且它是单输入单输出系统,其线性系统的传递函数模型则为:
MATLAB 控制工具箱中提供了tf()函数,该函数允许使用多项式系数来表示分子和分母,从而建立传递函数。这个功能有助于快速构建控制系统模型,以便进行进一步的分析和设计,其常用的调用格式为:
用MTALB 表示传递函数:
根据多项式系数求出传递函数模型的程序如下:
运行结果如下:
二阶控制系统是以二阶微分方程表示的控制系统,其中包括二个储能单元。电能在二个单元间传递,使其产生来回振荡的趋势。当阻尼值比较小时,系统就产生振荡特性。因此二阶系统在控制工程中运用很普遍,如电磁技术中的RLC 控制系统、机械系统中的弹簧、质量、阻尼系统,同时,在一定条件下的许多高阶系统,可以类似为二阶系统来研究。因此本文选择二阶系统展开研究。
以二阶系统为例介绍动态性能指标,二阶系统的动态性能指标主要有:上升时间tr、峰值时间tp、最大超调量Mp,延迟时间td、、调节时间ts。
典型二阶系统的结构图如图1 所示。
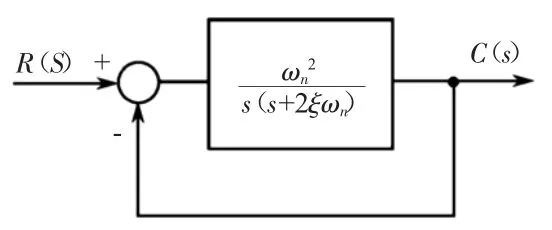
图1 典型二阶系统的结构
其闭环传递函数为:
式中:ξ为系统的阻尼比;ωn为系统的无阻尼自然振荡角频率为系统振荡周期。
使用MATLAB 绘制出频率ωn=3,阻尼比ξ=0,0.2,0.4,…,1.0,2.0 时的单位阶跃响应曲线图,程序如下:

如图2 所示,从图中分析可以得出:
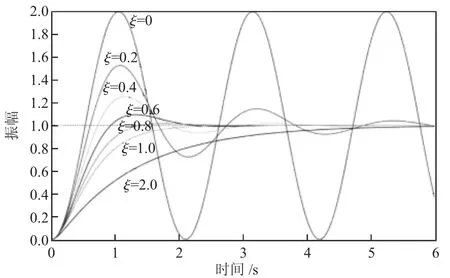
图2 不同阻尼的阶跃响应曲线图
ξ=0 时,系统为无阻尼状态,响应曲线等幅振荡。
0<ξ<1 时,系统为欠阻尼状态,阻尼比越大,响应曲线振荡减小,超调量也呈减小趋势,系统的稳定性也越好。
ξ=1 时,系统为临界阻尼状态,响应曲线呈单调上升趋势,没有超调量。系统稳定性好
ξ>1 时,系统为过阻尼状态,响应曲线呈缓慢上升趋势,没有超调量。系统稳定性好。
2 线性定常系统的稳定性
负半平面左侧全是该系统的微分方程的特征方程的根,或者系统的传递函数的极点都不位于右半平面,是一个线性控制系统保持稳定的充要条件。
已知系统的传递函数为:
在MATLAB 控制工具箱中提供了roots()函数,可用于直接计算多项式根,其常用的调用格式为:
应用roots()函数求解特征根时,如果特征多项式中缺少某次幂的项,那么在使用这个函数时,需要在对应的位置添加上系数0。
根据特征多项式,判断系统的稳定性需要求其特征根。程序如下:
运行后,其特征根如下:
通过上面的特征根的值可以看出只有负实部的特征根,故此系统是稳定的。
MATLAB 除了利用上面的求出特征根的方式来判断系统的稳定性还可以使用零极点图来判断系统的稳定性。
程序如下:
运行后,零极点即增益的值如下:
零极点如图3 所示。
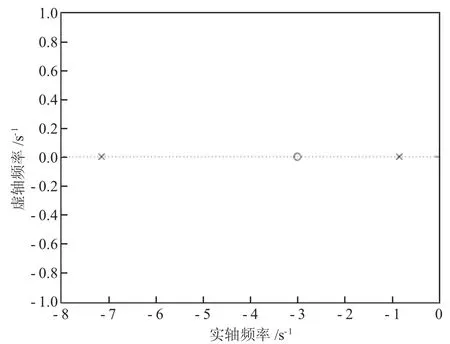
图3 零极点图
3 控制系统时域响应的性能指标
已知系统的传递函数:
对于这个二阶系统的节约响应进行评估,使用MATLAB LTI Viewer 工具箱可以便于直观地研究系统性能指标,具体操作步骤如下。
在MATLAB 程序中建立二阶系统闭环传递函数模型G。
在MATLAB 控制工具箱中提供了step()函数,可用于直接绘制动态系统的阶跃响应图,其常用的调用格式如下:
完整程序代码如下:
在命令行界面输入ltiview,即可启动LTI Viewer工具箱。
在“File”菜单中,选择“Import”,然后再导入系统数据对话框中[2],将上面创建的传递函数模型导入工作区域,从而获得系统单位阶跃响应曲线,如图展示。
在”File”的下拉菜单中选择“Page Setup”选项,可以对系统仿真时的打印输出和显示界面进行设置。
从图4 中可以得出在2.21 s 时,响应曲线达到顶峰,随后时间延长,曲线逐渐下降。继续增加时间,曲线呈现波动上升和下降的趋势,最终在3.4 s 时稳定。通过在曲线上右键单击,可以获得系统的性能指标:上升时间为tr=1.04 s,峰值时间为tp=2.21 s,ts=3.4 s。这表明,利用MATLAB 可以迅速、准确地从响应曲线中提取性能指标。
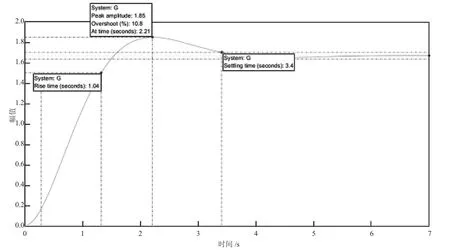
图4 阶跃响应曲线
4 Simulink 建模与仿真
Simulink 是MATLAB 核心组件之一,它能提供动态系统建模、仿真及进行分析。无需人来编写大量代码,只需要使用鼠标的操作,便可轻松地构建出复杂的系统。
Simulink 具有广泛的应用范围,其结构和流程清晰,仿真精确并且符合现实规律,具有高效能和敏捷性等优点。因此,Simulink 已在控制理论复杂仿真和设计中得到广泛应用。同时,Simulink 可以和许多第三方软件和硬件配合使用
用MATLAB 仿真与分析控制系统的步骤如下:
1)建立模型并确定仿真的输入输出参数;
2)设置仿真参数;
3)进行动态仿真并检查输出结果。
在此,使用Step 模块产生单位阶跃信号,比较环节采用Sum 求和模块,使用TransferFun 模块构造双击模块打开对话框设置Numerator 分子参数[35],Denominator 分母参数[1 2 0],校正环节也使用TransferFun 模块进行相对应的设置,使用Bus Creator 模块将三个输出信号合并成一个信号这样就可以在一个图像下显示出三个信号,方便进行比较观察,输出阶跃响应用Scope 示波器模块,仿真模型如图5 所示。

图5 SimuLink 仿真图
运行仿真前需要设置好仿真参数,显示系统的单位阶跃响应曲线需要双击Scope 模块。如图6 所示。
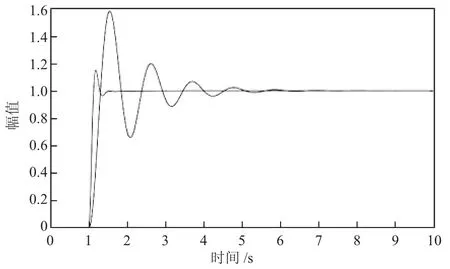
图6 Scope 显示波形图
5 根轨迹分析
控制系统的快速性、准确性、稳定性等问题,主要根据s 平面上系统的特征根的分布情况来判定,但是直接求取高阶系统的开环零极点很不容易,根轨迹法作为一种图解法,它不直接求解[1]。
闭环控制系统的准确性和稳定性主要取决于系统的闭环极点在s 平面上的分布。然而,对于高阶系统,特别是在系统分析和设计时,确定闭环极点是一个具有挑战性的任务,尤其是在系统分析或设计时,特征根的变化受到某些参数的影响,采用直接求根的方法就显得十分繁琐,难以实际应用。绘制系统的根轨迹可以通过自动控制原理的基本规则来进行粗略的绘制。
绘制根轨迹步骤如下:极点和零点;起点和重点;实轴区域的根轨迹;渐近线;分离点;入射角和出射角;虚轴交点。
上述几条规则虽然是人工绘制根轨迹的绘制步骤,但是人工绘图极为麻烦,正确率差,计算步骤较多,计算量大。并且在传递函数中的零极点如果发生改变,根轨迹的图也会随之改变,又得重新绘制图形。此时直接在MATLAB 软件的命令行中输入系统的传递函数,使用MATLAB 控制工具箱中的rlocus()函数,只需要编写几行代码绘制出根轨迹图的优势就凸显出来了[3]。其常用的调用格式如下:
已知系统的传递函数为:
用MATLAB 绘制系统的根轨迹图。
完整的程序代码如下:
运行结果如图7 所示。
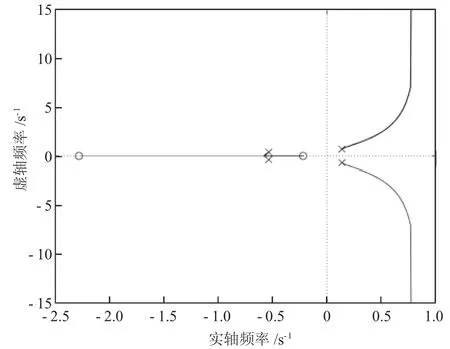
图7 根轨迹图
6 结语
传统的人工计算方法求解阶跃信号响应,稳定性、性能指标、稳态误差等这些问题计算非常的繁琐,本文根据系统的传递函数编写MATLAB 程序,便可以非常简单得到系统的阶跃响应图形,利用函数不需要人来进行计算便能判断出系统的稳定性,并根据图形分析控制系统的性能顺便得到系统的性能指标,使用Simulink 建模与仿真不需要实物,在系统中直接使用拖放式操作,方便简单地建立起直观的仿真模型。直接在电脑上就能进行分析,还可以看出利用Matlab可以更加形象生动的表现了系统的各种特性,并且加快了分析速度。

