基于多波束探测系统的海底地形测量

薛阳 张超 董雁南 詹华明

关键词： 多波束 海底地形图 三角网 规则网 精度评定

中图分类号： P229 文献标识码： A 文章编号： 1672-3791（2024）01-0001-04

海底地形测绘对于海洋开发、海洋工程建设以及海洋环境模拟具有重要意义。随着计算机技术、地理信息技术以及图像处理技术的飞跃式发展，海底地形三维可视化成为热点研究课题。杜跃等人［1］采用多波束的方法对海底复杂地貌进行识别，并通过滤波算法将波束传播噪声剔除，实现了复杂海底地貌的识别；马郑海等人［2］为提高水下测量的精度，采用多波束开展水下地形数据测量与模型建立，并在长江荆门江一段进行试验，结果表明：相对于传统测量技术，多波束水下测量精度更高；余启义等人［3］对海岛停泊水域、回旋水域水下地形进行测量，通过内外符合精度检测，结果表明SeaBat T20-P 多波束测深系统可高精度地获取水底地形数据。

1 多波束系统

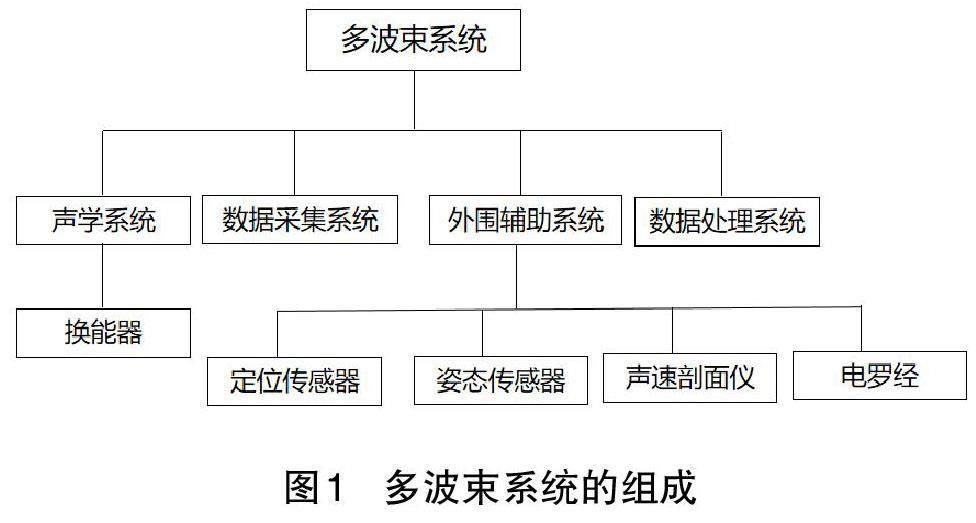
多波束系统是探测海底地形的专业测量系统，通过向海底发射声波信号，并接收从海底反射上来的回波，通过计算声波传输的时间，计算船底到海底的距离［4］。多波束系统通过向海底发射多条声呐，可以获得与船航线相垂直的多个点的水深值，并获得一条具有宽度的水深带，而多条水深带将整个区域的海底覆盖，形成海底地形数据。多波束声呐系统主要由4 个部分组成，分别是声学系统、数据采集系统、外围辅助系统以及数据中心处理系统［5］，具体如图1 所示。

1.1 工作原理

多波束声呐系统的两组换能器具有正交的特性［6］，可以在同一时刻发射多条波束，通过扇形的波束面记录对水底进行扫描的数据，再通过接收触底反馈的波束计算水深。换能器在测量船的底部，发射线呈扇面的形状向下发射波束，接收器将接收的声波转换成数字信号，通过不同角度的声波反射时间计算水深。

在测量过程中，声呐直接计算的水深值存在各种系统误差，不能直接反映具体水深，因此需将各类改正值添加到测量值中进行改正，多波束的测量水深值如式（1）所示。

1.2 数据处理

多波束测量系统可获得的数据包括水深值、位置坐标数据、测量时的姿态数据以及声速剖面数据等，为获取高精度的三维地形数据，需要对获取的原始数据进行预处理。在测量船工作过程中，由于仪器设备自身存在的系统误差与测量环境的影响，测量获取的数据中难免会存在各类误差和噪声，导致地形测量不准确。因此，在进行地形建模时需要剔除各类噪声，并对数据进行纠偏。

1.2.1 数据读取

读取原始数据并进行格式转换，满足数据处理软件的格式要求，对数据的来源进行注释。

1.2.2 声速剖面数据改正

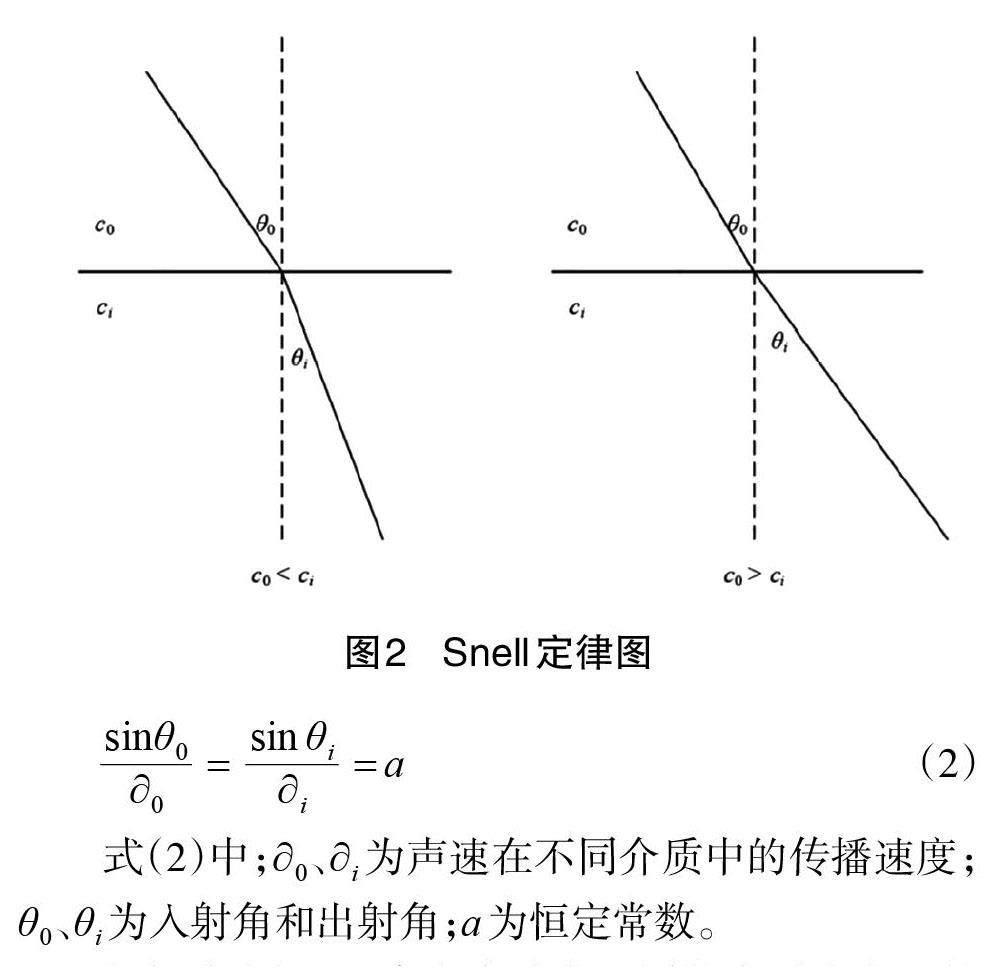
海水的温度、盐度等因素对声波的传播影响较大。在同一位置，海水的深度不同对声波的影响不同，因此多波束在海水中的传播线路并不是直线［7］。中间的波束为垂直向下，可看作一条直线，对于超过45°的波束，声波在传播过程中逐步产生了偏差，发生了折射现象［8］，成为一条曲线。因此，需要根据声速剖面对声线进行跟踪，计算新的测深值。随着海水深度的增大，声速发生的变化也越大，若只考虑声速在垂直面上发生的变化，则可采用声速垂直分层模型进行修正。声速剖面是分层模型的关键，在声呐测深系统工作时，声速剖面仪也开始对声速进行监测。在模型汇中，声速符合斯涅尔定律（Snell's law）如图2 所示。

根据式（2）可以求出声波在不同的介质中实际的传播速度，从而可以得到真实的水深值。

1.2.3 定位数据改正

测量船在航行过程中通过接收GNSS 信号进行精确的定位，由于大面积水域的电磁信号在传播过程中存在误差，因此需要对定位数据进行编辑，主要是剔除跳点数据并删除噪声点。工作人员可对因删除差异点造成的定位信息不连续现象进行点位数据内插，获取测量时具有相同间隔的连续定位信息，最终测量定位数据将以一系列相同间隔的点位数据表示。

1.2.4 姿态信息处理

姿态数据是指声呐系统在发射或接收声呐信息时所处的自身状态，包括各个方向的倾斜角度。在测量过程中，由于海浪、海风等因素的影响，声呐系统不可避免地处于摇摆的状态。因此，在数据解算过程中要修整姿态信息，加入旋转角修正系数，补偿船体姿态引起的测量误差。

1.2.5 潮位差修正

测量得到的数据是指换能器到海底的水深，也就是获取的高差数据，因此需要将水深转换到同一坐标系下的高程系统中，这就需要查阅测量时所在海域空间与根据测量的时刻计算的潮位资料，对测量数据进行潮位数据改正，得到正常的高程信息。

1.2.6 深度数据修正

海底地形的三维模型建立离不开准确的深度数据，而深度数据的精确度直接影响地形的精度。测量获得的水深数据存在很多假信息与噪声值，影响后续地形数据的搭建，因此需要對深度数据进行预处理，识别假信息并删除噪声点，得到精度较高的深度数据。

1.2.7 数据整理

将水深值、位置坐标数据、测量时的姿态数据、声速剖面数据以及其他改正数据等所有参数归算到最后的数据计算中，得到同一坐标系统中海底的精度较高的高程信息。

2 海底地形建模

2.1 规则格网法建模

在进行格网内插计算时，可设定格网单元的大小。根据测量要求的精度进行选择，格网间距较大，计算速度快，但地形表示不够精确，不能准确表达细微处的地形起伏。而格网太小，单元间距小，容易造成格网网点附近无测量值，内插时易产生错误，并且计算量大。因此，综合获取的数据与精度要求对格网单元大小进行设定。本文设置格网单元大小为0.5 m×0.5 m，格网大小为110 列×14 行，分别采用克里金法、反距离加权法以及自然邻点差值法进行建模，结构如图3 所示。

根据图3 所示的3 种不同规则格网发地形建模图可以看出，反距离加权插值法要比其他兩种方法建立的模型效果更好，克里金法和自然邻点差值法对条带的边缘区域地形进行了较为明显的拉伸。在建模时间上，反距离加权法用时最短，为3.56 min；克里金法用时接近，为3.86 min；自然邻点法用时最长，为7.52 min。

2.2 Delaunay 三角网建模

传统的三角生长法在计算形式上较为简单，但是需要大量的运算时间，故在此基础上对该算法进行优化成为众多学者的研究对象。研究者提出一种更加优化的合并算法，该算法将分治疗算法与逐点插入算法相结合，实现了算法的优化和互补。具体思路为以下几个方面。

（1）将数据点集按照分算算法的方式展开分割处理，按照点的横坐标和纵坐标分别进行排序形成点集，然后依照点的阈值分割为两个类似的子集。

（2）采用凸壳算法对点的横纵坐标分别提取最大值和最小值，提取的点作为初始凸壳，通过递归函数将剩下的点连接为完整的凸壳。将最小的x 值或者最小的y 值的点坐标读入凸壳点集，然后将起始点找到凸点连接为三角形，历遍所有的点，实现三角网的建立，如图4 所示。

（3）在初始三角网的基础上，通过数据内插将凸包内的点都插入到三角网中，生成新的三角网。插入的运算方法需满足Delaunay 三角网特征。合并子三角网直到迭代至最后的顶点位置。

Delaunay 三角网直接用采集的离散数据点作为三角形的三个顶点，与规则格网的内插数据相比，其精度相对更高，可较好地对地形的起伏特征进行表示。由于数据量较大，局部生成的三角网也比较复杂，如图5所示。

本文采用合成算法对数据进行处理，可节省大量的计算时间。对比传统的逐点插入法与合成算法的点位插入法，通过构网时间对比二者的计算速度，如表1所示。

从表1 中可以看出，合成算法的效率要优于传统构网算法，在进行大量离散点计算时可表现出极大的优越性，节省大量的数据处理时间。

通过合成算法处理获取的水深点，构建海底三维地形模型，相比于逐点内插算法获得的三维模型的精细程度更高，细节处表现更加精准，如图6 所示。

3 精度评定

对规则网法的3 种建模方式与合成算法的建模精度进行评定，采用点位中误差进行点位精度评价，中误差计算公式如下：

式（3）中：H_i 为模型内插点的水深值；S_i 为测量获取的点的水深值；n为检测点数。

在模型中采取20 个水深点进行中误差检测，计算4 种方法得到的中误差如表2 所示。

从不同的地形图建模方法中的误差对比可看出，4种建模方式的中误差值均满足海底地形图测量相关规范精度要求，Delaunay 三角网精度相对更高。

4 结语

多波速测量系统具有高精度、覆盖面积广、分辨率高的特点，是海洋地形测量的主要测量仪器设备。本文详细研究了多波束测量系统的测量工作原理，分析测量数据具有显著的大数据量、高密度、离散性等主要特点，并对数据处理流程进行详细阐述。通过采用规则网法与Delaunay 三角网建立海底三维模型，得出Delaunay 三角网建立模型速度更快，细节展示更精准的结论。最后，通过不同建模算法的坐标中的误差对比可知，Delaunay 三角网建模精度更高。