基于BCUSUM的多参数变点估计
王继梅,胡 尧,b
(贵州大学a.数学与统计学院;b.公共大数据国家重点实验室,贵阳 550025)
0 引言
回归模型是金融学、生物学、物理学等许多领域流行的数据分析工具。由于各研究领域的特性,模型中的一些参数可能会随着时间的推移而改变,因此时不变模型并不总是适用于整个数据集。一个好的模型应该具有解释整个数据集的灵活性,为了解决这个问题,可使用变点检测方法识别观测序列的参数变点,从而分割样本,再分别对每个子样本进行建模。关于单变点问题,目前已有一系列成熟的研究成果[1—3]。而多变点问题较为复杂,需要同时识别变点的个数和对应的位置。
Brown 等(1975)[4]提出基于递归残差的CUSUM(Cumulative Sum)检验,用于识别回归参数的不稳定性。Ploberger 和Krämer(1992)[5]提出基于OLS(Ordinary Least Squares)残差的CUSUM 检验,并将其与Brown 等(1975)[4]的方法在局部功效方面进行了对比。Deng 和Perron(2008)[6]研究了上述两种CUSUM 检验的非局部功效性质。Bai 和Perron(2003)[7]基于动态规划原则下的最小化残差平方和算法,提出循序检验法用于估计具有多个参数变点的线性模型。Chen和Nkurunziza(2017)[8]研究了变点数已知情形下的多变点问题。Jiang 和Kurozumi(2019)[9]提出基于最小二乘估计残差和递归残差的两个多元CUSUM统计量,但基于递归残差的统计量在备择假设下的功效较低。杨超等(2020)[10]提出合并带宽MOSUM(Moving Sum)检测方法。胡丹青和赵为华(2022)[11]基于贝叶斯后验推理及遗传算法研究了线性回归模型多结构变点(即参数变点)的变点检测方法。此外,许多变点检测方法的应用离不开有效的算法,如二元分割(Binary Segmentation,BS)[12]、隔离检测(Isolate-Detect,ID)[13]等。ID 算法变点检测的准确度较高,可将其拓展至多元回归模型的变点检测。
在变点分析领域,目前多数文献针对检验统计量的方法,尤其是在变点理论中广泛应用的CUSUM 统计量的基础上做了许多扩展和改进,但现有研究仍存在功效低、计算迭代时间成本高、小样本数据准确度低等不足。鉴于此,本文提出基于逆向累积递归残差和隔离检测技术的多元CUSUM检验方法,得到适用范围更广泛、检测效果更好的MCPDP(Multiple Change Points Detection of Paramter)变点检测算法。
1 多元CUSUM检验
基于参数设置,考虑如下线性回归模型:
其中,yt是响应变量,协变量xt=(xt1,xt2,…,xtk)′为k维列向量,回归系数βt是依赖于时间t的k维列向量,εt为不可观测的随机误差项。若式(1)中包含一个常数项,则对于任意的t,有xt1=1。
考虑如下假设检验问题:
其中,β是一个固定的k维列向量,g:R →Rk为有界的分段常值函数。若备择假设H1成立,则说明参数向量βt发生了变化,需对模型中存在的参数变点进行估计。
为了研究检验统计量的渐近性质,作以下假设。
假设1:
基于递归残差的一元CUSUM检验统计量已经有了一些研究成果,其中,Sen(1982)[14]证明了在原假设下该统计量弱收敛于标准布朗运动;Ploberger 和Krämer(1990)[15]推导出在备择假设下该统计量弱收敛于标准布朗运动加上协变量均值与结构突变的交互项,这说明一元CUSUM 检验的功效取决于协变量均值与参数变化方向的夹角,当二者正交时,将没有功效。为了克服这个困难,使用协变量与递归残差的乘积代替递归残差,考虑多元CUSUM检验,其检验统计量定义为:
在假设1下,多元序列xtεt满足多元泛函中心极限定理[16],类似地,也适用于基于递归残差的多元CUSUM过程。
定理1:设假设1和假设2成立。
(1)若原假设成立,则当n→∞时,有:
其中,⇒表示弱收敛,B(k)(r)是一个k维的标准布朗运动。
(2)若备择假设成立,则当n→∞时,有:
假设3:边界函数的形式为b(r)=λαd(r),且d(r) 连续,存在ε>0,使得对任意的r≥0 有d(r)>ε。
根据定理1、假设3和连续映射定理,可得:
若原假设成立,则当n→∞时,有:
若备择假设成立,则当n→∞时,有:
事实上,若仅关注特定的系数是否存在变点,则部分检验会有更好的检测效果。此时,H0:H′βt=H′β,其中,H是一个k×l的列满秩矩阵。考虑如下的部分CUSUM过程:
若原假设成立,且满足假设1 和假设2,则当n→∞时,有。因此,多元正向CUSUM 检验与下文的BCUSUM 检验可以基于改进的构造适用于部分检验的检验统计量。
2 多变点估计算法
2.1 BCUSUM检验
尽管多元CUSUM检验可以解决协变量均值与结构突变正交时一元CUSUM 没有功效的问题,但该检验在备择假设下的功效并不好,其原因是变点产生之前的递归残差期望为0,变点产生之后其期望不为0,于是变点之前的递归残差不含有用信息,这些残差过程将表现为纯随机游走过程,此种累积方式会增加噪声,从而使得变点检测效果较差。因此,为了提高功效,改善变点估计性能,可通过逆向累积递归残差构造检测器,即BCUSUM,其定义如下:
若||BQt,n||在t=1,…,n中至少有一次大于边界函数bt=λαd((n-t+1)/n),则拒绝原假设,相应的最大统计量为:
根据定理1、假设3和连续映射定理,可得:
若原假设成立,则当n→∞时,有:
若备择假设成立,则当n→∞时,有:
接下来,根据式(4)和式(7)研究CUSUM 和BCUSUM检验在备择假设下的渐近功效性质。考虑一个简单的情形,βt=β+n-1/2g(t/n),其中,g(r)=cI(r≥τ*),c∈Rk,τ*表示变点位置,I(·)是示性函数。由h(r)的表达式可知:
图1给出了CUSUM和BCUSUM检验在k=1时的渐近功效曲线。模拟实验重复次数设为100000 次,由下文可知,两种检测方法的检验水平是不同的,故使用调整检验水平为5%的临界值,研究备择假设下检测方法的渐近功效。图1(a)至图1(e)表明,除了变点发生时刻特别靠前之外,BCUSUM的检验功效都比CUSUM检验功效高,且变点位置越靠后,其优势越明显。此外,从图1(f)中可以看出,对于固定的,若变点τ*位于样本量的320 之后,则BCUSUM检验比CUSUM检验有更好的变点估计性能。
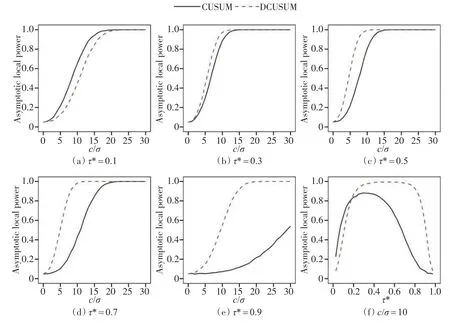
图1 渐近功效曲线
在基于BCUSUM检验识别出模型存在结构突变后,需要确定变点的具体位置。对于βt=β+δI(r≥τ*)(δ≠0)的单变点模型,可采用极大似然估计量,然而,当变点位置靠后时,会出现较大的估计误差。为了解决这个问题,可通过逆向累积递归残差构造估计相对变点位置的统计量。||BQ[rn],n|| 渐近正比于||h(1)-h(r)||,当0 <r<τ*时,||h(1)-h(r)||为常值;当τ*≤r≤1时,||h(1)-h(r)||为单调减函数。若利用||BQ[rn],n||的渐近标准差对其进行缩放,则该检测器将渐近正比于将正比于式(9)(根据式(8)可得)。
式(9)在r=τ*处取得最大值。因此,考虑:
定理2:令βt=β+δI(t/n≥τ*),δ≠0,且满足假设1,则对于τ*∈(0,1],当n→∞时,有。
根据h(r)的表达式、定理1 及连续映射定理可得,定理2表明变点估计量是τ*的相合估计。
2.2 MCPDP算法
BCUSUM检验是针对单变点情形展开的,然而多变点问题是统计应用中常见的问题,为了使上述变点检测方法适用于此类问题,可结合隔离检测技术来估计变点个数及位置。该技术能避免包含多个变点的区间、允许在可能很小幅度的频繁变化的情况下进行检测,以及计算复杂度较低,从而提高变点检测的准确性和降低其计算成本。鉴于该技术的诸多优势,本文将其拓展到回归模型的参数变点检测,提出MCPDP算法。MCPDP是按照一定的步长以左右交换的形式向中间扩展检测区间,判断是否有变点的一个过程。假设模型存在N个参数变点,对每一个变点τj(j=1,…,N),MCPDP 可分为2 个阶段:阶段1 是将τj隔离在一个区间,使得该区间不再包含其他变点;阶段2 是利用式(5)中的检测变点τj。其基本思想可概括如下:
针对回归模型的多参数变点检测问题,本文提出的MCPDP 算法是基于快速、准确的隔离检测技术且在变点发生时刻靠后时检测也高效的BCUSUM检验。在给定δn、λα和(s,e]的情况下,MCPDP算法的步骤如下页表1所示。

表1 MCPDP算法步骤
3 模拟研究
本文通过数值模拟讨论BCUSUM 检验的有限样本性质,主要分析不同变点位置和样本量对检验水平与功效的影响,以及使用一系列的评价准则来说明MCPDP 算法的优良性。数据由两种情形下的模型产生:
情形1:yt=1+utzt+εt,t=1,…,n。
情形2:yt=ut+0.5yt-1+εt,t=1,…,n。
其中,ut=0.9I(t/n≥τ*),zt=(1+0.5L)et,L是滞后算子,et与εt独立且服从于标准正态分布。情形1和情形2分别对应整体和部分结构突变检验,其中,H=(1,0)′。
设样本量n=120,500,2000,9000,显著性水平取α=0.05,对于不同情形、方法和样本量取值的每种组合,模拟实验重复次数设为10000次。表2给出了原假设下检验水平的结果,其中,sup W表示的是Andrews(1993)[17]提出的sup-Wald检验统计量,调整参数为0.15,该方法具有弱最优性。从表2 中可以看出,CUSUM、BCUSUM 和sup-Wald的检验水平均接近于显著性水平0.05,部分存在一些扭曲。在不同情形下,无论样本量多大,相比于CUSUM和sup-Wald,BCUSUM都较好地控制了检验水平。
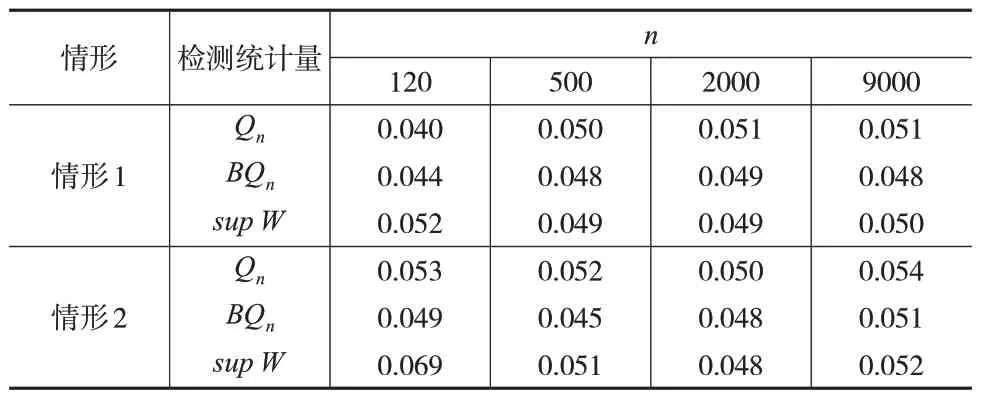
表2 检验水平
设变点相对位置τ*=0.1,0.3,0.5,0.7,0.9,对n与τ*取值的每个组合,设置模拟次数为10000 次。表3 给出了备择假设下功效的结果。从表3中可以看出,除了τ*=0.1之外,BCUSUM检验相比CUSUM检验都有更好的性能,尤其是在样本量较小时;sup-Wald检验具备弱最优性,尽管CUSUM 检验的功效比sup-Wald 检验的功效低得多,但是BCUSUM 的逆序累积结构弥补了CUSUM 的不足,BCUSUM 检验与sup-Wald 检验有相似的性能,因此BCUSUM检验具有较好的功效性质;在有限样本中,变点位置对检验方法的影响与理论结果一致;仅从样本量的角度来比较功效可以发现,样本量越大,功效越大,最终所有方法的功效都趋近于1。
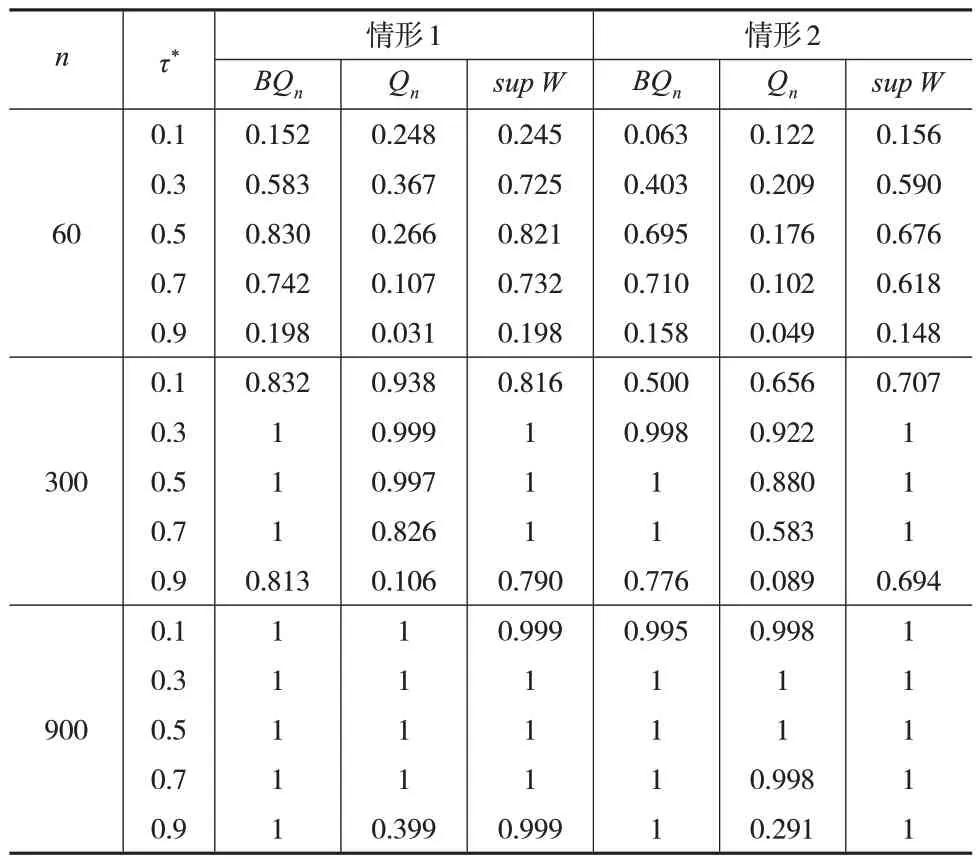
表3 功效对比
为了说明MCPDP 算法的有效性,将该算法与另外两种变点检测算法的变点估计性能进行比较,其中第一种算法是Bai 和Perron(2003)[7]提出的BP 算法,第二种算法是Jiang和Kurozumi(2019)[9]提出的多元正向CUSUM单变点检验算法,本文利用ID技术实现了多变点检测。为此,设置模拟数据如下。
情形3:yt=ut+εt,t=1,…,n
其中,数据长度n=300,500,900,εt~N(0,0.22),变点位置向量τ=([0.278n],[0.452n],[0.486n],[0.6n],[0.618n],[0.666n]),各个区段均值u依次为-0.18、0.08、1.07、-0.53、0.16、-0.69、-0.16。
针对模拟数据,为评价变点检测算法性能,采用Hausdorff距离(dH)、F_score及兰德指数(Rand Index)作为综合评价指标,dH取值越小或F_score 及Rand Index 取值越大,表明算法性能越好。此外,还比较了不同算法的程序运行时长。每种情形分别进行5000次模拟,评价指标均采用均值表示,模拟结果见下页图2。

图2 算法在情形3下不同数据长度的模拟结果
4 案例分析
交通三参数(流量q、速度v和密度k)表征交通流特性,他们之间的成对关系通常被称为交通流理论的基本关系或基本图(Fundamental Diagram,FD),在交通建模与交通管理中至关重要。考虑到道路交通情况复杂多变,交通数据异构多源,时空相依性强,原有的工程经验确定性基本关系模型q=kv有较大的局限性,本文探究交通三参数的动态关系,并将交通条件、交通环境、车辆、驾驶员、驾驶行为等影响因素作为随机扰动纳入模型中。通过实际交通数据识别交通参数变点,揭示交通流的演变规律,从而验证本文方法的有效性。
数据来源于贵阳市交通管理局。以贵阳市观山湖区长岭北路与东林寺路交叉口交通流量和交通速度为研究对象,选取2021年3月8日至2021年3月14日一周的交通流量和速度数据,按采集粒度5min 统计,每天有288 个数据量。以2021年3月9日(周二,工作日)和2021年3月13日(周六,非工作日)的交通流量和速度数据为例,图3 展示了这两日的三维FD。从图3 中可以看出,随着时间的变化,交通流量与交通速度的线性关系是动态变化的,因此,不再基于历史数据静态建模,而是在本文所提模型框架下研究该数据的参数变点,这样更符合实际情况。

图3 三维FD
将交通速度作为自变量,交通流量作为因变量,构建回归模型。经MCPDP变点检测算法检测,2021年3月9日存在三个变点,分别是06:30、07:15和19:35(具体结果见表3)。根据实际情况分析,变点产生的原因可能是:06:30与07:15 对应的是两个早高峰时刻,这可能是受到人们早上出行上班、上学处在不同拥挤时段的影响,交通流波动较大,19:35处于下班、休闲娱乐等活动的晚高峰时期。根据速度系数取值,可以发现都是正值,因为速度系数对应的是交通密度,取值非负,在时段(07:15,19:35]内的速度系数最高为24.8518,即该时段的交通流量相对较高,这与实际相符。表3中的第2行是利用所有数据建立交通流量关于交通速度的回归模型,拟合优度只有0.6628;表3 中的其余行是利用相邻变点间的数据进行线性拟合,拟合优度显著提升,说明带有变点的模型能更好地捕捉数据的动态变化,对数据的刻画更贴切。
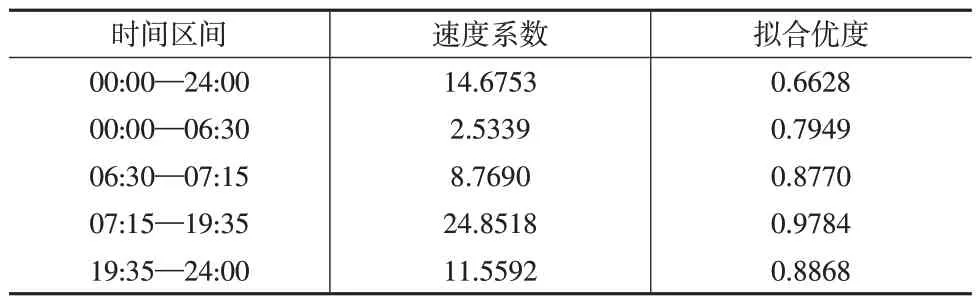
表3 2021年3月9日的变点估计结果
2021年3月13日存在四个变点,分别是00:45、06:20、07:15和20:55(具体结果见表4)。其中,00:45可能是由部分工作者在周五下班后进行夜间朋友聚会等休闲娱乐活动造成的,06:20 和07:15 时人们早起活动、购物或出游等造成了新波动;20:55时人们开始夜间的消遣娱乐活动,再次引起交通状态的变化。此外,和表3 的结果相似,经变点检测后,带有变点的模型的拟合效果更好。

表4 2021年3月13日的变点估计结果
综上可知,工作日和非工作日交通参数的基本关系存在较大差异,在同一路段的不同时段产生不同的交通流变点,交通管理部门可对工作日和非工作日的交通采取不同的调控措施。实证结果说明了本文提出的变点检测方法可快速且有效地检测变点数量及位置,交通数据变点检测结果所对应的时间符合实际交通情况,可以较好地解释引起交通流波动的原因,这可以为相关部门提供参考依据。此外,原有交通参数的确定性经验关系不切合道路交通实际分析需求,而建立随机模型有利于降低后续FD 等模型的估计和分类偏差。
5 结束语
本文提出了基于递归残差的逆序性质和隔离检测技术研究回归模型中多参数变点的检测方法。首先,针对协变量均值与偏移量正交导致损失功效的问题,探讨了多元CUSUM检验及其渐近性质,进一步研究部分检验。其次,考虑到正向累积递归残差功效较低,引入修正的检验统计量BCUSUM,分析其渐近性质,进而得到基于BCUSUM 的变点估计量。最后,结合隔离检测构建MCPDP算法,快速检测数据的变点个数和位置。模拟研究和实例分析表明,本文所提方法在变点估计性能方面表现较好,为相关理论研究提供了参考依据。随着技术的发展,近年来许多领域对在线变点检测方法的需求急剧上升,因此,如何将该方法扩展为在线变点检测方法是下一步的研究方向,快速监测变点并报警对于减少损失、降低风险具有重要意义。

