剪力滞对CFRP 板-钢梁加固界面应力的影响

朱佩云，李晓章，余明明，谢旭

(1.浙江大学 建筑工程学院，浙江 杭州 310058；2.昆明理工大学 建筑工程学院，云南 昆明 650500)

采用焊接、栓接或者铆接钢板的加固方法，虽然能够提高钢结构的承载能力和刚度，但因施工难度大、增加结构自重及加固工艺复杂等原因，存在加固成本高、施工对交通影响大的不足[1].随着碳纤维增强复合材料（CFRP）在土木工程中的应用日益扩大，近年来国内外学者开始探索利用粘贴CFRP 的方法加固钢结构的可行性[2-6].与金属材料相比，CFRP 具有轻量、高强度、耐腐蚀、抗疲劳等优点，其作为钢结构加固材料使用时具有明显的优势[7-9]，不仅可以避免焊接热影响和栓接孔应力集中的问题，而且具有运输和施工简便、施工期间的交通荷载对施工质量影响小的优点.

CFRP 加固钢结构技术是通过黏结薄层将结构应力传递至CFRP，使CFRP 分担加固部位钢结构应力的方法.Nozaka 等[10-14]的试验研究表明，黏结层剥离破坏是加固结构的易损部位，黏结层的性能与力学行为是建立CFRP 加固设计方法的关键.不少学者通过试验研究分析黏结层的破坏形式和失效机理，基于弹性应力解析、有限元数值模拟分析，研究黏结界面的受力分布特征[15-20].

为了分析钢结构加固后CFRP 板黏结界面的应力状态，Smith 等[21]提出粘贴CFRP 板的简支梁在均布荷载和集中荷载作用下的界面应力计算公式，此后不少学者在此基础上进一步研究其他荷载条件下的CFRP 板界面应力计算方法.邓军等[22]推导了温度作用下的界面应力计算式，石川敏之等[23-24]给出预应力CFRP 板的界面应力计算式，Stratford 等[25]提出同时考虑温度和预应力作用的界面应力计算方法.除此之外，石川敏之等[26]推导了简支梁在端部仅受到弯矩时CFRP 板边缘产生的切应力和法向应力，分析纯弯矩作用对黏结层应力的影响.

上述研究均不考虑剪力滞变形对界面应力计算的影响.薄壁梁弯曲变形在上、下翼缘会产生剪力滞而改变翼缘的弯曲应力分布，特别是对于宽翼缘钢梁而言，剪力滞对结构弯曲应力的影响是不可忽视的因素[27-30].

为了分析工字钢梁弯曲变形产生的剪力滞变形对黏结层法向应力和切应力的影响，本文采用能量变分法，建立考虑剪力滞影响的CFRP 加固梁平衡方程.通过与试验结果对比，验证理论公式的精度.分析受到弯曲变形的简支梁及悬臂梁的CFRP 黏结层切应力和法向应力，讨论剪力滞效应对界面应力计算结果的影响，为CFRP 加固钢结构时的界面应力计算提供参考.

1 基本理论及有效性验证

1.1 研究对象及基本假定

以图1 所示的单侧粘贴CFRP 板的工字型钢加固梁为对象，研究剪力滞效应的影响.为了简便起见，假定梁上、下翼缘对称.坐标轴x、y 和z 分别沿梁的纵向、横向及竖向.梁截面的几何尺寸如图1 所示，下翼缘粘贴CFRP 板，ta和tp分别为黏结层和CFRP 板的厚度.

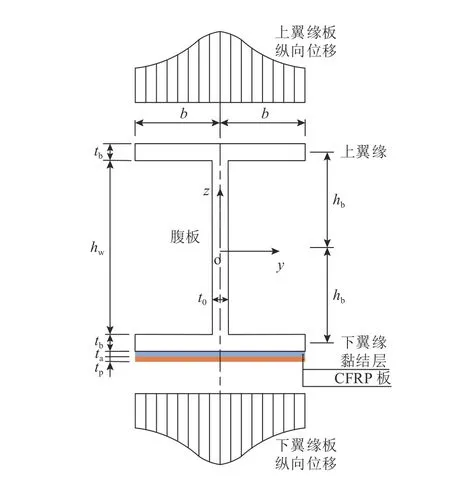
图1 截面几何参数及薄板纵向位移假定Fig.1 Cross-sectional geometric parameters and longitudinal displacement assumptions for thin plates

在加固梁应力计算理论方程的推断过程中，给出如下假定.

1)应力处于弹性阶段，不考虑塑性影响.

2)翼缘及CFRP 板纵向位移沿宽度方向呈曲线分布，假定剪力滞引起的纵向位移沿y 向为3 次曲线分布[31-33]，如图1 所示.

3)钢梁腹板变形符合平截面假定，只考虑纵向弯曲变形，忽略竖向剪力引起的剪切变形.

4)钢梁竖向挤压应力σz、翼缘板平面外的剪切变形γxz、γyz忽略不计，梁在平面内变形，仅考虑纵向应变εx和纵向剪切变形γxy产生的应变能.

5)黏结层的剪切变形沿厚度方向均匀分布，εx、γxy及法向应变εz均以平均值代替，忽略板厚方向变化的影响.

6)CFRP 板的剪切刚度忽略不计，只考虑轴向刚度的影响.

1.2 梁截面的位移场及应变

1)钢梁截面的位移和翼缘应变.

钢梁翼缘板上、下相同，采用相同的纵向位移差函数，梁挠度w 及纵向位移u[31-33]可以分别表示为式中：下标1、2 和3 分别表示上、下翼缘和腹板，上标“′”表示对坐标x 求导，φb(x)为剪力滞引起的翼缘板纵向位移差.由于翼缘板的纵向变形关于z 轴对称，以下仅给出y 轴正方向对应的量，在y 轴负方向的量按对称考虑.

根据几何方程可知，钢梁各部分纵向应变εx和翼缘板切应变γ分别为

2)CFRP 板的位移及应变.

由于钢梁弯曲变形时黏结层会发生法向和切向变形，下翼缘CFRP 板的位移与钢梁翼缘板不同，竖向挠度η 和纵向位移up分别为

式中：φp(x)为剪力滞引起的CFRP 板纵向位移差.CFRP 板为各向异性材料，仅考虑纤维方向的力学性能，纵向应变εxp可以表示为

3)黏结层的位移及应变.

黏结层的厚度较薄，假定厚度方向的变形为线性变化，上、下面的变形与钢梁和CFRP 板的变形一致.黏结层的纵向位移为钢翼缘板与CFRP 板的平均位移，剪切变形为两者的相对值.纵向应变εxa及切应变γxa分别为

法向应变εza为

1.3 梁弯曲变形的平衡方程

根据最小势能原理可知，处于平衡状态的结构在虚位移上的体系总势能U 的一阶变分为零，即

如图2 所示为加固梁弯曲变形时梁微元体的内力和黏结层界面应力.图中，下标b、a、p 分别表示钢梁、黏结层和CFRP 板，σa、τa分别为黏结层界面法向和切应力，M、V、N 分别为弯矩、剪力和轴力.

图2 梁微元体的内力和黏结层界面应力Fig.2 Internal forces of infinitesimal structure and interfacial stress of adhesive layer

加固钢梁的应变能为钢梁、黏结层和CFRP板应变能之和.各项可以表示为

弯曲变形梁的外力势能为

在代入各应变的计算式后，体系总势能可以表示为

要使总势能取得极值，由变分原理[26]可得

得到基本微分方程

以及边界条件

均布荷载作用下的简支梁在x=0 及x=l 处的边界条件为

对于x=0 为固定端、x=l 为自由端的悬臂梁，固定端和自由端的边界条件分别如下所示：

1.4 精度验证

为了验证上述理论推导的有效性，通过简支工字形加固梁静载试验结果的对比进行验证.

1.4.1 CFRP 板加固工字钢梁的静载试验装置 根据国内市场CFRP 板的供应情况，采用中奥碳纤科技（苏州）有限公司生产的CFRP 板和黏结剂，加工了一根长为2 m 的工字形钢梁，钢材为Q355.CFRP 板、钢梁和黏结剂的材料参数如表1 所示.表中，E 为弹性模量，v 为泊松比.

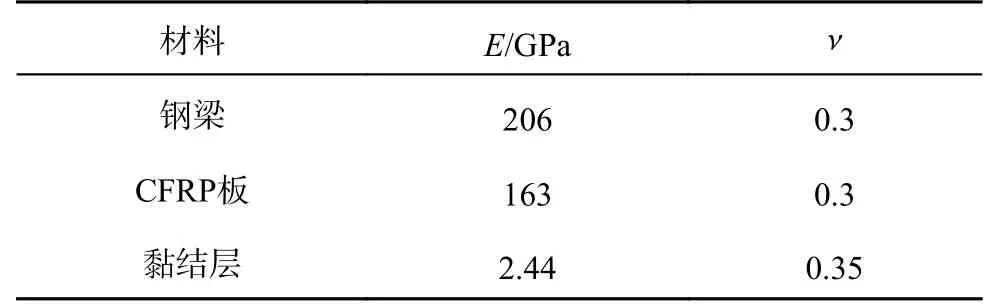
表1 试验梁的材料参数Tab.1 Material parameter of test beam

如图3 所示为均布荷载作用下的简支梁底粘贴CFRP 板构件示意图.其中ta=1 mm，tp=2 mm，tb=6 mm，t0=6 mm，b=50 mm，hb=150 mm.如图4所示为现场试件及试验装置图.使用柔性绳子悬吊砝码的方式，模拟均布荷载.一个标准砝码的质量为20 kg，共计44 块，分11 个悬吊点，对应的换算均布荷载为4.8 kN/m.分3 级加载的方式逐渐增大试验荷载.

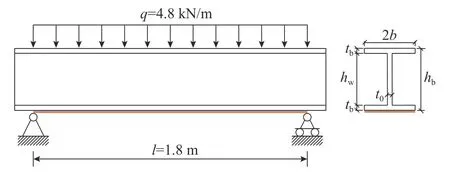
图3 均布荷载作用下的加固简支梁Fig.3 Reinforced simply supported beam under uniform load

图4 试件及试验装置图Fig.4 Figures of specimens and test devices

由于黏结层界面应力无法直接测量，选择CFRP 板表面和钢梁下翼缘板上表面布置应变测点，沿梁长在距离支座0.3、0.6 和0.9 m 处布置应变片，测量静载下对应点位的轴向应变.如图5 所示为断面上应变片测点的纵、横向位置，其中CFRP 板表面均匀布置5 个应变片；钢梁下翼缘板上表面受到腹板位置的影响，在y=b 及y=b/2 处左、右对称布置4 个应变片.应变片尺寸为2 mm×3 mm.断面1-1、2-2、3-3 分别表示距离支座0.3、0.6 和0.9 m 的截面.

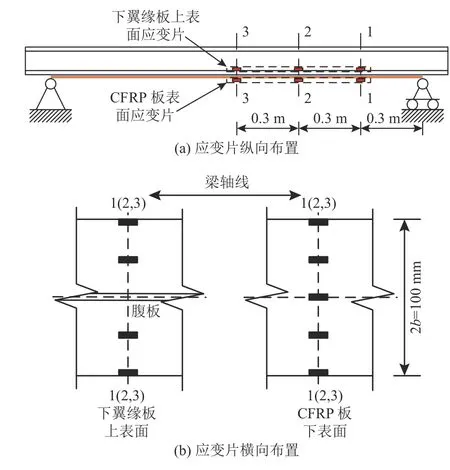
图5 应变片布置和测点Fig.5 Strain gauge arrangement and measuring point

1.4.2 结果对比 除了与试验结果对比以外，利用通用有限元软件ABAQUS6.14.4，计算加固结构的应力作为参考.钢梁和胶黏剂采用8 节点六面体线性减缩积分实体单元(C3D8R)，若CFRP 板也采用实体单元离散，则为了考虑其弯曲刚度，在厚度方向需要分成多层，仅CFRP 板的单元数量达数百万，庞大的单元数量影响计算正常进行.为了减少计算量，采用四节点曲面薄壳单元(S4R)模拟CFRP 板，与采用实体单元的胶黏剂之间用“tie”的接触条件结合.试验梁的网格尺寸通过收敛性验证确定，网格尺寸为1.0 mm，胶黏剂在厚度方向划分为4 层.如图6 所示为有限元计算模型，单元数量约为156.4 万，节点数量约为170.5 万.

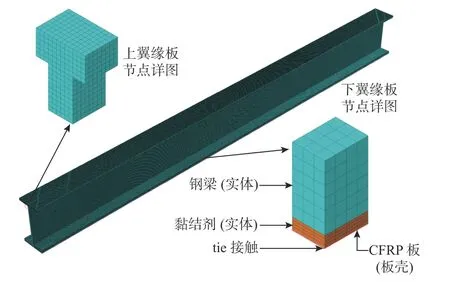
图6 试验梁的有限元模型Fig.6 Finite element model of test beam

CFRP 板表面在y=0 处沿梁长的应变结果对比如图7(a)所示，钢梁下翼缘板上表面y=b/2 处沿梁长的应变结果如图7(b)所示.图中，理论值为利用本文推导的计算公式得到的结果；x 为梁的轴向，支座为坐标原点.从图7 可知，试验、理论和有限元三者的应变结果基本一致，但有限元数值总体上较试验值和理论值偏大，相对误差最大为10.91%.

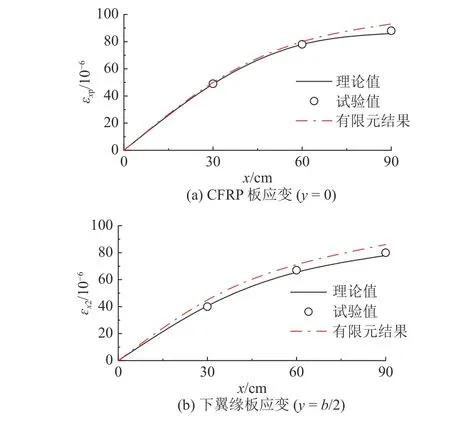
图7 CFRP 板和钢梁下翼缘板沿梁长的应变Fig.7 Strain of CFRP plates and lower flange plate of steel beam along beam length

断面3-3 是跨中截面，故应变相同，剪力滞为0.断面1-1 和2-2 的应变结果对比分别如图8、9 所示.图中，y 为梁的横向.从图8、9 可知，均布荷载简支梁越靠近支座，剪力滞效应越明显；CFRP 板的应变均大于对应的钢梁下翼缘板；有限元结果总体上比试验值和理论值大，试验结果和理论值基本吻合.

图8 CFRP 板应变Fig.8 Strain of CFRP plates

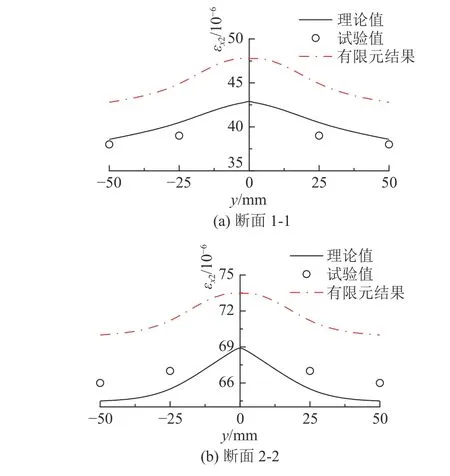
图9 钢梁下翼缘板的应变Fig.9 Strain of lower flange plate of steel beam

通过简支梁试验与精细有限元对比分析，验证了理论方法的正确性.相对而言，试验结果更接近于理论结果，各断面应变的有限元结果与其他两者的结果误差较大.这可能是因为有限元计算分析采用了“tie”接触方式，影响了应变的计算精度.

2 剪力滞效应对界面应力的影响分析

2.1 界面应力计算

由于CFRP 板较薄，利用高弹模CFRP 板加固，有利于提高加固的效果.采用高弹模CFRP 板，分析简支和悬臂梁在均布荷载作用下的界面应力及剪力滞的影响.

2.1.1 均布荷载作用下梁端附加弯矩的简支梁为了模拟加固梁在实际作用状态下剪力滞对界面应力的影响，以梁端受弯矩作用的简支梁为对象进行分析.如图10 所示为均布荷载作用下梁端附加弯矩的简支梁底粘贴CFRP 板.ta=1 mm，tp=2 mm，tb=8.5 mm，t0=5.6 mm，b=50 mm，hw=191.5 mm；各材料的参数如表2 所示.表中，E11、E22分别为沿纵向和横向的材料弹性模量，G12为切变模量.

表2 加固梁的材料参数Tab.2 Material parameters of reinforced beam

图10 均布荷载作用下梁端附加弯矩的加固简支梁Fig.10 Reinforced simply supported beam with bending moment applied at each end under uniform load

翼缘中心A 和边缘B 处的黏结层界面法向应力σa和切应力τa如图11 所示.图中，x 为梁的轴向，跨中为坐标原点.

图11 简支梁两端附加弯矩ql2/10 时的黏结层界面应力Fig.11 Interfacial stresses of adhesive layer in simply supported beam with bending moment ql2/10 applied at each end

结果表明，在翼缘中心A 和边缘B 处的法向应力σa相同，翼缘中心A 和边缘B 处的切应力τa相差较大，但无论计算点位是翼缘中心A 还是边缘B，用CFRP 板加固的简支钢梁在端部的界面应力远大于中间，因此端部界面应力计算是否正确关系到加固结构是否可靠有效.

为了计算剪力滞对界面应力的影响大小，对比了最大界面应力在考虑和不考虑剪力滞影响下的结果，如图12 所示.为了考虑翼缘板宽度的影响，计算了ql2/10 弯矩作用下翼缘板宽和CFRP 板宽度取一半时对应的界面法向应力和切应力，如图13 所示.结果表明，翼缘板越宽，剪力滞越明显，且考虑剪力滞后，端部界面应力均有所增加.

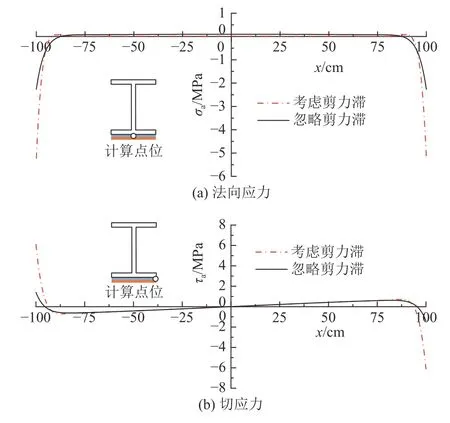
图12 宽翼缘板简支梁两端附加弯矩ql2/10 时的黏结层界面应力Fig.12 Interfacial stress of adhesive layer in wide flange plate simply supported beam under bending moment ql2/10 applied at each end

图13 窄翼缘板简支梁两端附加弯矩ql2/10 时的黏结层界面应力Fig.13 Interfacial stress of adhesive layer in narrow flange plate simply supported beam under bending moment ql2/10 applied at each end

2.1.2 均布荷载作用下的悬臂梁 如图14 所示为受到均布荷载作用的悬臂梁.结构在受拉的上翼缘粘贴CFRP 板，材料参数及截面几何尺寸与上述简支梁相同.

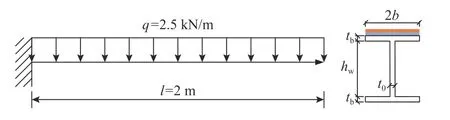
图14 均布荷载作用下的加固悬臂梁Fig.14 Reinforced cantilever beam under uniform load

如图15 所示为利用本文理论方法得到的最大界面应力纵向分布的结果.经计算发现，悬臂梁剪力滞的影响结果较小，此处仅给出考虑剪力滞时的应力结果.图15 中，在横截面上的各点正应力σa相同，同时分别给出τa在翼缘中心A 和边缘B 处的对应值.从图15 可知，界面应力在悬臂梁固支板端急速增大，在梁中间及自由端的应力接近于零.

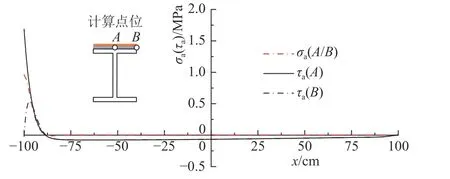
图15 悬臂梁中黏结层界面的法向和切应力Fig.15 Interfacial normal and shear stresses of adhesive layer in cantilever beam

2.2 参数分析

为了分析不同弯矩下剪力滞对界面应力的影响，以图16 所示梁端受弯矩作用的简支梁为对象进行分析.在梁底粘贴CFRP 板，ta=1 mm，tp=2 mm，tb=8.5 mm，t0=5.6 mm，b=50 mm，hw=191.5 mm.材料参数如表1 所示.假定端部的弯矩为ql2/40、ql2/30、ql2/20 和ql2/10.

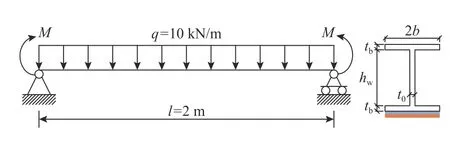
图16 梁端施加弯矩和均布荷载作用下的简支梁Fig.16 Simply supported beam under bending moment applied at each end and uniform load

如图12 所示为在ql2/10 弯矩作用下的截面法向应力和切应力，如图17 所示为端部界面应力随附加弯矩M 的变化.可知，端部界面的应力明显大于内部截面，有弯矩作用的端部界面应力大于无弯矩作用的位置.这表明CFRP 板的剥离始于端部，法向应力是不可忽视的因素；截面内力是引起界面剥离的重要因素；截面内力越大，越容易剥离，且剪力滞的影响随着截面内力的增大而增加.

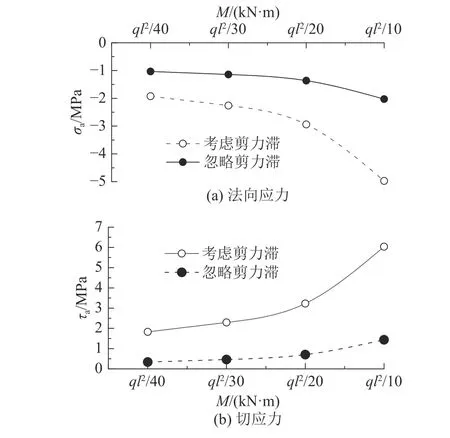
图17 端部界面应力随附加弯矩的变化Fig.17 Variation of end interfacial stress with additional bending moment

3 结 论

(1) 通过与试验和精细有限元结果对比，在能量变分法计算中假定剪力滞引起的翼缘板纵向位移沿y向3 次曲线分布是合理的.

(2) 在CFRP 板粘贴区域的端部，剪力滞影响不可忽视，且随着截面弯矩和翼缘板宽度的增加而显著.

(3) 端部应力明显大于中间应力，加固设计时正确计算端部应力十分重要，应适当增大黏结层的设计应力.