基于耦合神经网络的步态识别方法

沈 喆, 盛 阳

(沈阳航空航天大学民用航空学院, 沈阳 110136)

2022年10月,《信息安全技术 步态识别数据安全要求》(GB/T 41773—2022)正式发布实施。由于生活中某些特定的场所对安全等级有特殊要求,但是由于人员数量比较庞大,且实际情况较为复杂导致了传统的生物特征身份识别很难继续发挥效能[1],环球网2019年报道的“步态识别:50米外,秒读你的‘活体密码’”,通过人的体型以及走路姿态来识别行人身份的步态识别技术,相比于其他类似人脸、指纹等传统生物特征进行身份识别方法来说其具有无需近身识别和极不易被模仿的优点[2]。现在普遍使用的步态识别方法按照研究图像类型不同分为基于非模型识别方法与基于模型识别方法[3-4],其中非模型识别方法直接从人体轮廓中提取步态特征,通过构建步态轮廓图的帧与帧之间的关系针对步态图像的轮廓信息进行分析,利用步态样本轮廓得出步态特征。与模型步态识别法相比较,非模型步态识别方法具有模型简单、整体算力低等优点,对目标图像或者视频的分辨率要求更低,也是如今步态识别主要采用的方法。非模型步态识别法不需要考虑人体内部骨架等结构如何运动,重点研究这些轮廓信息的外部轮廓动态方式,研究步态图像中步态轮廓像素量的变化量,根据变化量得到对应的步态特征来实现步态识别。刘晓阳和靖薇[5]顺利将步态识别运用于识别煤矿井下人员身份,采用自适应的度量学习实现特征提取,为煤矿井下人员提供位置自动化检测;Derlatka和Borowska[6]提出异构基分类器集合的方法进行步态识别,并提高了准确率与识别时间。

1 图像预处理

1.1 形态学处理

实验采用CASIA-B数据库中经过运动目标提取且二值化后的图像,虽不需要进行行人检测以及背景剔除,但仍存在噪声、粘连等问题,要对这些二值化的图像进行形态学处理。其中膨胀操作可以将图像中的物体变大,使它更加连通;腐蚀操作则可以将图像中的物体变小,使它更加细化;开运算可以做到去除噪点,将图像边缘的锯齿消除;闭运算可以填补图像中物体的孔洞。腐蚀:A⊙B={x,y|(B)xy⊆A},膨胀:A⊕B={x,y|(B)xy∩A≠∅},分别表示用一个B结构来腐蚀A图像和用一个B结构来膨胀A图像。⊙和⨁分别表示腐蚀操作和膨胀操作,(x,y)为锚点的位置,x和y为结构元值为1的像素相对锚点的位置偏移。

1.2 图像的归一化

由于步态数据采集过程中设备是固定不动的,采集到的图样是由小到大再到小的状态,图像中也因此存在过多噪声点,而步态归一化[7]通过成比例调整步态轮廓的高度,把图像中步态轮廓的中心位置和大小调整至一致。通过找到图像中上下左右像素值的最值点,由此生成一个足以覆盖步态轮廓的最大矩形框,通过矩形框裁剪出人体目标的轮廓图像,将其高度放缩至64像素并保持此横纵比不变来实现。如式(1)所示计算调整轮廓图的质心标xc。归一化操作也可以优化步态图像中特征受到的外界背景环境以及采样光照的影响,解决步态图像中局部过暗过亮的问题,抑制住了步态图像中的干扰噪点。

(1)

式中:xc为轮廓图质心坐标;xi为像素值为1的点的横坐标;N为整幅图中像素值为1的点的总数。

2 步态能量图

步态能量图[8]的原理是使用多通道映射函数来使步态图像的更多时空信息在均值的过程中保留下来,通过选取人的一只脚脚尖刚离地到另外一只脚脚尖刚离地这一段时间作为一个步态周期,使用一个周期内步态序列轮廓图求一个平均灰度值图像,根据式(2)得出步态能量图。

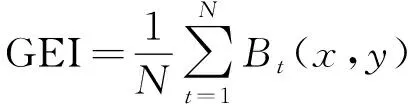
(2)

式中:N为一系列步态轮廓序列的个数;t为当前时刻的序列图;x、y为图像坐标。

图1为一个步态周期和其步态能量图,图中像素点越亮的部分代表其在步态周期中出现得越频繁。

图1 一个步态周期以及步态能量图

3 主流CNNs方法

普通卷积神经网络模型(CNNs)通常由卷积层、池化层、下采样层、全连接层和输出层组成。将图像作为输入量输入到第1个卷积层中,将卷积层的输出作为激活函数。然后通过添加池化层来减少输入参数量,在输出层得到输出值之前,经过的卷积层有助于提取特征。CNNs中的输出层属于全连接层,来自其他层的输入向量在全连接层被平化,这一步的作用是方便后续输出转换为卷积神经网络需要的参数量。

卷积层对图像各个子区域进行特征提取,使用激活函数对消除高层偏差后输出的特征向量进行转换,卷积层特征提取计算公式为

Ft=ReLU(wt⊗Ft-1+βt)

(3)

式中:Ft为模型提取输出的特征向量;Ft-1为子区域输出的特征向量;wt为偏差权重;βt为偏差向量,线性整流函数(ReLU)作为激活函数,定义为ReLU=max(0,x),其中x为神经网络的输入。

这里的池化层的作用是克服卷积时对位置的敏感,通常采用最大值池化或平均值池化。在绝大多数应用情景下,最大值池化提取特征能力较强,maxP表示最大池操作,操作定义为

Fi=maxP(Fi-1)

式中:Fi-1为池化区域内的输入像素点;Fi为区域内特征的集合。

4 耦合神经网络模型

耦合神经网络[9]包括双层卷积神经网络、对比损失层[10]和逻辑回归损失层,如图2所示。图2显示,来自卷积层的特性向量,通过全连接层输出至对比损失层,通过识别输入样本类别来训练网络模型参数。其将从上层提取的步态特征向量与Conv4区分并连接,对比损失层每次输入一对图片,进入同一个网络进行特征提取。对应到图中就是上下均为一对。那么两个网络就会提取两个特征,然后可以用这两个网络输出的特征进行相减来提取特征差异,然后再经过全连接层作一个二分类,判断输入图像是否为同一人,最后耦合神经网络通过损失函数组合训练。这里使用损失函数还可以帮助识别模型是否存在过拟合或欠拟合的情况,如果损失函数在训练集上较低但在验证集上较高,可能表示模型存在过拟合。

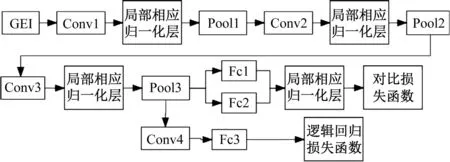
GEI为步态能量图;Conv1、Conv2、Conv3为卷积网络单元;Pool1、Pool2、Pool3为池化层;Fc1、Fc2、Fc3为全连接层

GEI作为样本输入到卷积网络单元Conv1中,扩张操作后输入到局部归一化层N和Pool1中。卷积网络单元Conv2与Conv3对池化层的输出量获取步态特征向量的方式一样,将卷积单元Conv3经过池化层Pool3得出的特征向量输入到Fc1和Fc2中,然后输入到局部响应归一化层当中,对比损失层输入得到的特征向量。接下来,通过对来自Pool3输出层的两个特征图进行差分融合,将卷积网络的Pool3输出层的特征向量分别输入到Conv4和对比损失层,将其映射为0～1分布,确定步态样本输入的相似度。

5 网络训练方法

结合逻辑回归[11]和对比损失函数[12]对网络进行参数训练,训练后提取样本步态特征来进一步实现对比、识别行人身份。经过全连接层归一化后的特征向量输入到对比损失层中,其中对比损失函数的定义如式(4)所示,α为手动设置的阈值,用来计算网络中两个输出向量之间的度量距离。

(z)+:max(z,0)

(4)

式中:I1、I2为样本对的差值特征向量;Lc为通过网络特征提取预测到的差值特征向量的概率分布;y为两个样本是否匹配的标签;d为两个样本特征之间的欧氏距离;z为设定的阈值。

在卷积网络单元Conv4中输入得到的特征向量进行差值融合,把Fc3输出的特征向量输入到逻辑回归损失函数中,并基于0～1分布实现对输入步态样本的身份识别。逻辑回归函数常用于二分类,损失函数越小,模型在训练集上面的拟合效果越好,逻辑回归损失函数如公式(5)所示,其中θ的最优值可以通过梯度下降的方法,得到的θ在训练集中的拟合效果非常好,但是可能会存在过拟合的现象,这时可以使用L1、L2正则化的方法来降低过拟合带来的影响。

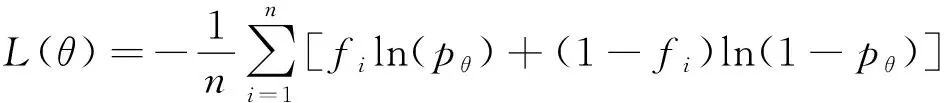
(5)

式中:n为输入样本数量;i为目标类;pθ为损失层参数;fi为真实目标样本差值特征向量的概率分布。

耦合神经网络的参数由损失函数关联法驱动,并通过一个特定的参数λ将两者结合起来,从而控制损失函数在总损失函数中的实现状态,二者联合如式(6)所示。

Loss=L(θ)+λLc

(6)

λ取值范围为(0,+∞),在模型训练过程中,当λ=0时,损失函数的检验与网络参数的匹配无关;当λ≠0时,验证损失函数生效,逻辑回归损失函数与网络参数拟合的比例逐渐减小。可以看到,当λ→+∞时,可以看作对比损失函数单独涉及对整体参数的调整。经过实验发现当λ=0.06时,该参数下的损失函数组合优化的性能最优,步态识别率也得到提高。

6 实验分析

实验运用MATLAB 2017-a仿真工具,操作系统为Windows 10,设备内存容量16GB,CPU为酷睿i5-1340p,采用中科院CASIA-B步态数据集作为训练集。CASIA-B数据集是使用最广泛的步态数据集,包含124个受试者的步态轮廓数据,每个受试者有10组视频。每个受试者的步态序列样本分别采集自0°,18°,…,180°的11个角度,每个视角下都有10个步态序列。选择在4种正常步态条件下收集的步态序列作为训练样本,记为NM1-4。选择了两个行走序列作为验证样本,记为NM5-6。验证样本集选择大衣遮挡下的步态序列(CL1-2)与背包遮挡下的步态序列(BG1-2),通过参数λ将两个损失函数联合训练网络参数。图3为耦合网络模型对正常行走、背包遮挡以及大衣遮挡下的步态识别率。通过图4可以看出,在背包情况下耦合网络对各视角的识别综合情况要好于CNNs。

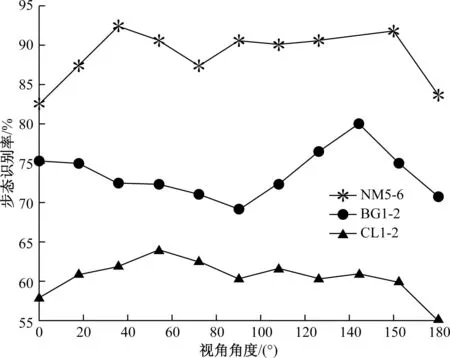
图3 耦合在各情况下的识别率

图4 背包情况下CNNs与耦合网络识别率对比

对CNNs[13]的识别数据与通过本文使用的耦合神经网络得出的结果进行综合对比,见表1。

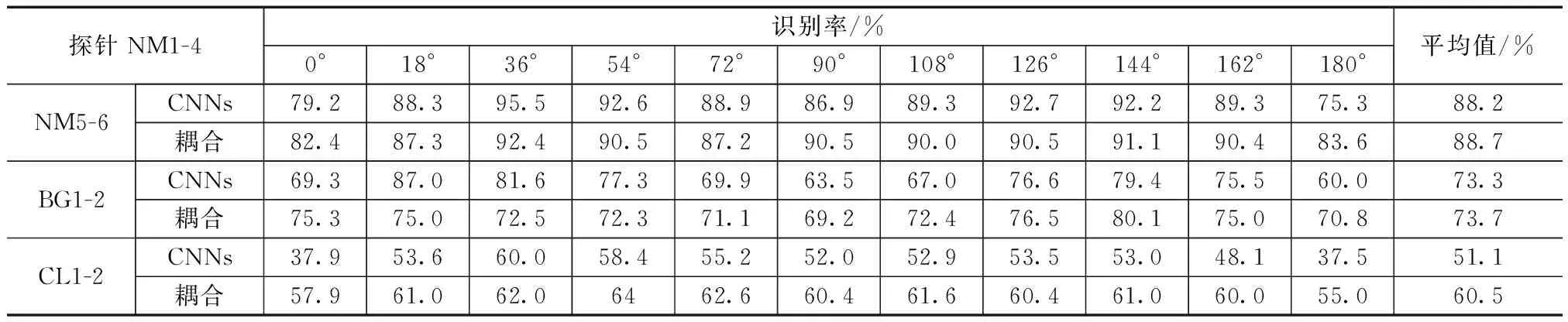
表1 不同视角下不同条件步态识别率

由表1可以看出,耦合神经网络的平均识别率要高于CNNs,在考虑11个不同视角下的NM、CL、BG 3种不同的行走情况时发现,在某些行走情况和视角,如探针为NM、BG条件下的18°～72°时,耦合网络识别率低于CNNs。CNNs对该一段视角的识别更加稳定,但是耦合网络模型综合性能优于CNNs,证明了模型的有效性。通过损失函数联合训练参数可以有效解决步态识别中最小的类间距离大于最大的类内距离的问题,有效提高了在不同视角下的步态识别率。

7 结论

提出基于耦合网络模型的步态识别方法,介绍了步态识别的原理以及耦合神经网络的基本架构,对CASIA-B数据集所提供的步态图像进行图像归一化等处理并由此得出步态能量图,将得到的步态能量图输入到构建的耦合神经网络模型中提取步态特征差异,构建对比损失函数和逻辑回归损失函数,并经过训练得出λ,使得损失函数联合优化的性能达到最优,使用训练后的网络模型来进行步态特征识别比对,能够有效提升步态识别精度。最后,通过实验得出耦合神经网络在验证样本集NM5-6、BG1-2以及CL1-2上的步态识别率,并与传统CNNs进行实验结果对比,验证了步态识别时当角度发生变化或人物出现外物遮挡时,耦合神经网络模型可以有效地减少步态识别效果的误差。