平均几点钟怎么求
顾森

晚高峰指的是,傍晚时分城市道路的交通量突然增大的现象,了解一座城市的晚高峰时间,对个人的出行安排以及整座城市的交通规划都有很大的帮助,例如,某城市最近5天晚上拥堵指数最高的时候分別发生在17:00,18:00,17:00,16:30,19:00.平均算下来,晚高峰的时间是几点呢?你或许会说,这还不简单?算一算17,18,17,16.5,19的平均数不就行了吗?(17+18+17+16.5+19)÷5=17.5,因此晚高峰的平均时间就是17:30.乍一看,这个逻辑似乎没有问题,可仔细一想,好像有点儿不对——照这样算,23:00和半夜3:00的“平均数”就应该是(23+3)÷2=13,也就是13:00.但是,夜里的两个时间点平均下来怎么变到下午去了?实际上,这两个时间点的正中间应该是半夜1:00,拿它当这两个时间点平均后的结果要合理一些,再看一个更加复杂的例子吧,假设有6:00,14:00,22:00这三个时间点,它们的“平均数”似乎是(6+14+22)÷3=14,也就是14:00.但这三个时间点均匀地分布在一天当中,两两之间都间隔8个小时,并没有呈现出什么“集中趋势”.
你是不是有些迷茫?其实,这一切都是因为,“几点钟”这样的数量和“有多长”“有多重”“有几个”这种类型的数量不一样,它是不断循环的.它们并不是分布在数轴上的,而是分布在一个圆圈上,你既可以说23点比3点晚20个小时,也可以说3点比23点晚4个小时.它们之间并没有大小之分.在这种情况下,我们就得重新思考平均数的定义了,同样地,盘点某景点的旺季平均在几月份,统计某山区一段时间内的平均风向,都会遇到类似的问题.
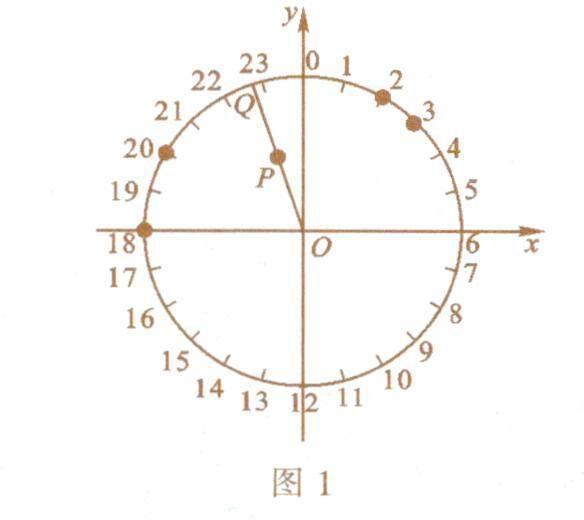
这类问题的平均数究竟该怎样定义呢?数学家们想到了一个好办法.假设我们想要求出20:00,18:00,3:00,2:00的平均值.我们要依次完成下面的步骤(如图1).
(1)在平面直角坐标系上,以原点O为圆心,作一个半径为1的圆.
(2)找出圆上的24个等距点,把最上面的那个点记作0.接下来的点按顺时针方向依次记作l,2,3,…,23.它们分别表示0:00,1:00,2:00,…,23:00.
(4)求出所有横坐标的平均数,以及所有纵坐标的平均数.所有横坐标的平均数为[-0.866+(-1)+0.707+0.5]÷4≈-0.165,所有纵坐标的平均数为(0.5+0+0.707+0.866)-4≈0.518.
(5)把上一步得到的两个数当作一个新的点的横、纵坐标.在平面直角坐标系上标出这个点.在我们的例子中,这个点是(-0.165,0.518).我们将其记作点P.
(6)连接OP并延长,与圆交于点Q.点Q在圆上的位置就表示这些时刻的平均数.在我们的例子中,Q点位于22和23之间,到22的距离和到23的距离大致是5:1的关系.所以,20:00,18:00,3:00,2:00的平均数大约就是22:50.
想一想,利用这样的方法来计算23:00和3:00的平均值,是否真的就是1:00?你也可以用这个方法来计算6:00,14:00,22:00的平均数.你会发现,点JP的坐标是(0,0),跟点O是重合的,因此我们无法连接OP并延长.这种情况下,我们就说它们的平均数无意义.这与我们之前的直觉是相符的.
这样,我们看到了如何将统计学中一个最简单的概念移植到循环类数量中.统计学中还有许多其他概念,例如中位数、方差,以及高中大家将会学到的正态分布、相关系数,等等.它们是否也能运用到循环类数量当中呢?如果能的话,怎样重新下一个定义最合适呢?针对这些问题,数学家们开创了一个统计学的分支,叫作“定向统计学”.感兴趣的同学不妨在图书馆或互联网上查阅相关的资料,作进一步的研究.
2024年1-2月号“数学潜能知识竞赛”参考答案
1.C 2.C 3.B 4.3 5.-14 6.970
2024年1-2月号“数学潜能知识竞赛”获奖名单
(括号内为辅导老师)
王麒霖 陈宇童(唐晓燕) 王峻熙 常逸璇 袁子和 黄懋洋 李或博
辛梦琪 吴恺琳(梅莹) 翟天泽 郑峻泽 韩依姗(高洁)
- 中学生数理化·八年级数学人教版的其它文章
- “数据的分析”易错题专练
- “数据的波动程度”专项突破
- “数据的集中趋势”知识演练
- “数据的分析”新题总动员
- 当当闯关记
- 自律带来自由

