2-CPR/RPU并联机构的构型设计及工作性能分析

丰晓东, 赵耀虹, 李瑞琴, 贺阳涛, 张磊

(中北大学机械工程学院, 太原 030051)

较近年来,并联机构在机械加工、运动模拟、包装生产等领域的应用日渐广泛,相比于串联机构,并联机构由于结构紧凑、重载多载、精准稳定等[1-2]特性颇受重视,具有很高的可行性和实践应用价值。物流包装产线现今单量增势明显,为提高分拣配送效率和精度,缩短人工周期成本,并联机构足以适用大多数货件流水线的分拣封装要求。

并联机构已成为高刚度、高精度或者较大载荷需求领域内的研究热点,并在相关方面取得一定进展。李佳霖等[3]对3-RSR并联机构在球副处添加角度传感器,分析其运动特性,解决了解析法的全部解中会出现复数根和无效根的问题。李泽辉等[4]提出一种具有3个平动自由度的2-CRR/UPU并联机构,计算该机构的位置逆解并进行速度分析。贺阳涛等[5]设计一种2-PCR_2-UPS非对称的并联机构,结合MATLAB与Adams分析其运动过程具有连续性和平稳性。Du等[6]对U-PRU-PUS并联机构采用雅可比代数法进行运动学正、逆解分析,通过自适应遗传算法优化该并联机构的结构参数。Chablat等[7]设计一种两自由度的并联机构2USP-U,分析其两组设计参数下直接运动学解的个数。Song等[8]分析一种具有2R1T运动性能的对称3-UPU并联机构,并对其进行尺寸优化。王韬略等[9]提出2T1R三自由度的双层并联机构,与Adams仿真对比验证运动学模型的正确性。林浩等[10]针对育秧机中铺盘调节机构的应用需求,提出一种平行支链的3-PPR并联机构,并展开运动学研究。郝亮亮[11]利用MATLAB和比例积分微分(proportional integral derivative,PID)控制仿真分析3-PRC并联机构的数学模型,优化锂电池包装机的运动精度。武晓轩等[12]以2UU-UPU并联机构为研究对象,使用蒙特卡洛法求解工作空间并研究了结构参数变化对工作空间的影响。Han等[13]对2P3RR并联机构的工作空间边界奇异、内部奇异、结构奇异进行研究,验证该机构不具备奇异位形。马春生等[14]基于2-UPR/RPS并联机构动静平台尺寸及运动副布局的改变,分析其对工作空间的影响。于红英等[15]研究了3-RPS并联机构的运动学正逆解与工作空间,验证了以支链角度分析位置与工作空间的正确性和可行性。Khalifa等[16]提出了一种3自由度的并联机械手,利用运动/力传递率指标对工作空间进行评估,验证其运动性能的可行性。上述研究由于机构自身运动特性以及工作空间的限制,使得在实际工程应用中无法同时实现较大的转动角度和工作范围。

目前物流分拣装箱方式仍是以人工分拣或半自动机械分拣为主,灵活程度相对较低,仍需人员调配协助。故提出一种具有3自由度的2-CPR/RPU并联机构,可满足物流工程中不同规格货件的拣选需求,提高分拣工序的自动化效率。

1 2-CPR/RPU机构构型及自由度分析

2-CPR/RPU并联机构是由静平台、动平台、1条RPU支链以及2条CPR支链组成。其中,CPR支链分别与静平台对应两边相连且呈对称排布,圆柱副C的轴线与其同分支的转动副R轴线平行,由移动副P相连RPU支链中虎克铰U位于动平台一边的中心位置上,R副轴线与相邻的C副轴线相垂直,如图1所示。

图1 2-CPR/RPU并联机构Fig.1 2-CPR/RPU parallel mechanism

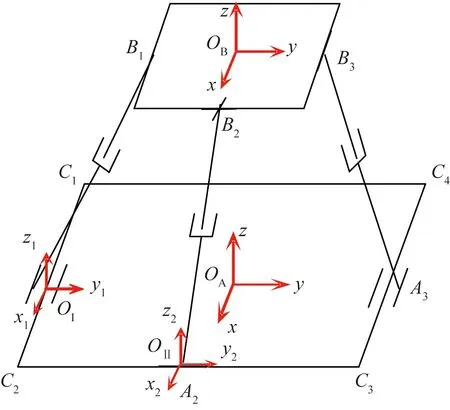
图2 2-CPR/RPU并联机构坐标系Fig.2 Coordinate system of 2-CPR/RPU parallel mechanism

基于螺旋理论[17]对2-CPR/RPU并联机构的自由度进行求解,首先先将该机构支链分解,然后对各支链分别进行局部坐标系建立并展开。对支链RPU建立局部坐标系OⅡ-x2y2z2,如图2所示,其y2轴沿R副轴线方向与静坐标系y轴平行,z轴垂直向上,依据右手定则确定x2轴方向,可知运动螺旋系为

(1)

式(1)中:$1～$4为RPU支链的运动螺旋;c、s分别为移动副在x2和z2方向的单位矢量分量。

对式(1)求约束反螺旋可知,支链RPU的约束螺旋系为

(2)

由于CPR两条支链关于x轴对称排布,因此对其中一条分支建立局部坐标系OⅠ-x1y1z1,如图2所示,其x1轴沿C副轴线方向与静坐标系x轴平行,可知其运动螺旋系分别为

(3)

式(3)中:$1～$4为CPR支链的运动螺旋;e、f分别为移动副在y1和z1方向的单位矢量分量。

对式(3)求约束反螺旋可知,支链CPR的约束螺旋系为

(4)

结合式(2)、式(4)可知,2-CPR/RPU并联机构的公共约束螺旋系,对其反螺旋求解可得到机构的运动螺旋系为

(5)

式(5)表明机构共有3个运动螺旋,即有3个自由度,分别是沿z轴方向上的移动,绕x轴方向的转动以及沿x轴方向的移动。

利用修正的Kutzbach-Grübler公式[式(6)]对并联机构的自由度进行解析计算。

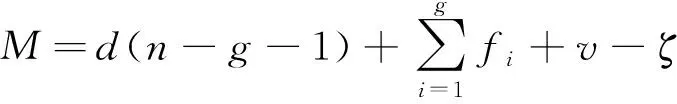
(6)

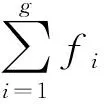
结合式(2)和式(4)可知,机构存在一公共约束,即d=5;存在一过约束,即v=1;不具备局部自由度,故ζ=0;则求解可知M=3,与螺旋理论所判断机构具有3个自由度的结果相符合。

2 2-CPR/RPU机构位置逆解

位置逆解是指已知动平台上确定一点的位置姿态输出求解机构中输入表达式的过程。该机构的运动学逆解为已知静平台{OA}坐标系下,动平台{OB}坐标系中点OB位姿(xyzαβγ),求取各杆输入杆长参数l1、l2、l3的值,采用封闭矢量[18]对机构支链进行逆解分析。

2.1 RPU支链运动学逆解

已知静平台中心OA、动平台中心OB、动平台尺寸等长为2r、定平台尺寸等长为2R、A2B2为RPU分支中移动副的位移量。

在静坐标系OA-xyz中,A2的坐标为

A2=(R,0,0)

(7)

动坐标系OB-xyz中,B2的坐标为

B2=(r,0,0)

(8)

采用z-y-x欧拉角表示动平台点Bi相对于静平台点Ai的旋转变换矩阵R,设动平台绕OB-z轴转动的角度为γ,绕OB-y轴转动的角度为β,绕OB-x轴转动的角度为α,则旋转矩阵R可表示为

(9)

式(9)中:c为cos;s为sin。

可知,B2在静坐标系下用B′2表示,则有

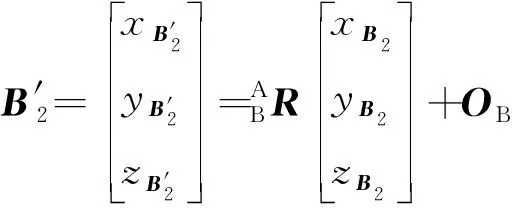
(10)

由于机构在运动过程中无绕y轴和z轴方向的转动自由度,故β=0,γ=0,解得B′2表示坐标为

B′2=(r+x,y,z)

(11)

支链RPU存在约束方程l2=|B′2-A2|,求解可知逆解。

(12)

2.2 CPR支链运动学逆解

对两条CPR支链进行分析,CPR-Ⅰ、CPR-Ⅲ支链C副具体位置沿x轴方向,且位置随动平台同时移动无法确定,建立相应外积关系为

(13)

(14)

在OA-xyz坐标系下,点Ci(i=1,2,3,4)为

C1=(-R,-R,0),C2=(R,-R,0),

C3=(R,R,0),C4=(-R,R,0)

(15)

由于两条CPR支链中运动副的轴线均平行,A1B1OB处于同一平面内且与C副轴线相垂直,同理,A3B3OB也处于同一平面内,点Ai(i=1,3)坐标为

A1=(x,-R,0),A3=(x,R,0)

(16)

动坐标系OB-xyz中,Bi(i=1,3)的坐标为

B1=(0,-r,0),B3=(0,r,0)

(17)

通过式(9)旋转变换可得点Bi(i=1,3)在{OA}坐标系下的坐标为

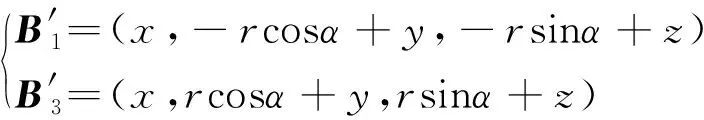
(18)

机构本身存在的约束关系为

(19)

式(19)中:C1C2、C2C3分别为静平台相邻两边的边长矢量;A1OB为动平台几何中心到圆柱副C的距离;A2OB为动平台几何中心到转动副R的距离。

解得y=-ztanα。

由式(13)～式(19)可得杆l1、l3的逆解方程分别为

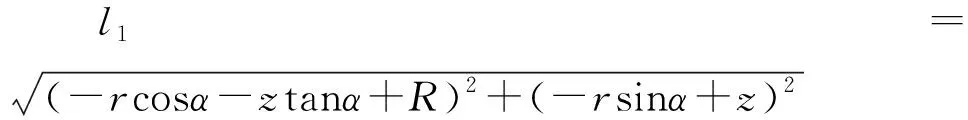
(20)

(21)

3 速度雅可比矩阵分析

Jacobian矩阵反映的是执行器末端即动平台输出空间的速度与各关节驱动输入空间的速度映射关系,对该机构进行速度分析。

用已知的机构运动逆解方程组对等式两侧关于时间t同时求导,推导输入与输出的速度表达式为

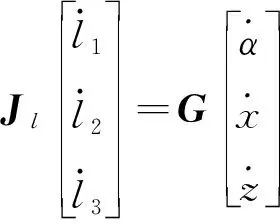
(22)

式(22)中:Jt和G可分别表示为

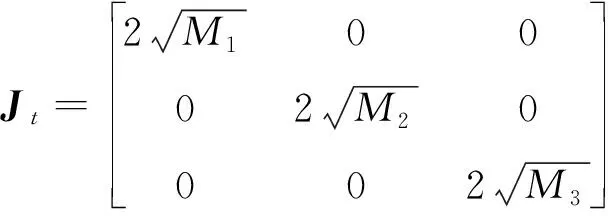
(23)

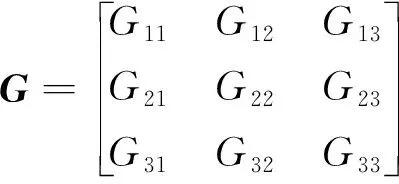
(24)

式(23)中Jt的各矩阵元素Mi可表示为

(25)

式(24)中G的各矩阵元素Gii可表示为

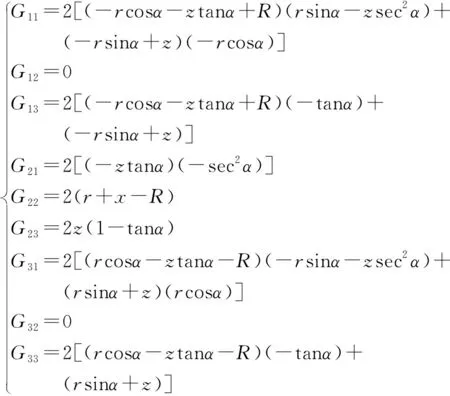
(26)

若Jt非奇异即|Jt|≠0,则有映射表达式为

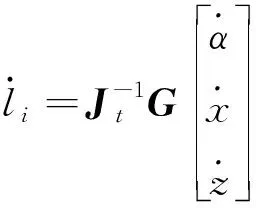
(27)

4 机构奇异性分析

奇异性作为并联机构运行过程中使得输出运动处于一种临界状态的固有特性,其存在则会导致机构运动性能一定程度的影响。处于奇异位形的机构正常运动受阻,稳定性下降亦或位姿改变致使自由度发生变化,都会使机构无法正常工作。机构奇异主要有运动学逆解奇异、正解奇异及混合奇异3种情况,可通过雅可比矩阵中的Jt和G是否为奇异矩阵进行分析判别。

4.1 逆解奇异

|Jt|=0,|G|≠0时,则会引起机构逆解奇异。机构各支链驱动输入位移为0,执行器末端(动平台)受约束处于临界卡死状态,称为边界奇异。计算可知|Jt|=0存在有3种情况,即

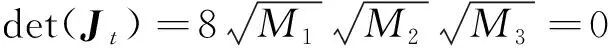
(28)

分析可知,机构各驱动支链的角度以及位移具有限制,li(i=1,2,3)不会出现为0的情况,则z≠0,故不会出现逆解奇异。

4.2 正解奇异

|Jt|≠0,|G|=0时,则会引起机构正解奇异。计算可知|G|=0存在有2种情况,具体如下。

(1)第一种情况可表示为

2(r+x-R)=0

(29)

求解得到x=R-r,支链Ⅱ则同时垂直于动静平台,结合机构尺寸不符合此条件,不会发生此类奇异。

(2)G的矩阵元素G1i(i=1,2,3)和G3i(i=1,2,3)对应成比例,求解得到r=0,R=0,结合机构尺寸不符合此条件,因而该机构不存在正解奇异。

4.3 混合奇异

|Jt|=0,|G|=0时,则会引起机构混合奇异。基于以上所述,同时满足上述所有条件才可能出现混合奇异,此时机构将失去全部自由度。由于机构自身尺寸条件限制,故该机构不会发生混合奇异。

综上所述,2CPR/RPU并联机构在给定结构尺寸的运动过程中不存在3种奇异位形。

5 工作空间

工作空间即为执行端机构所能到达的位置集合,能够直观地将机构实际工作性能的优劣占比进行衡量[19]。支链驱动副的移动范围,旋转副角度的转动程度以及机构是否奇异都将作为直接影响工作空间的主要因素。以2-CPR/RPU机构动平台作为参考点,采用数值搜索法[20],给定机构的设计参考值:静平台边长为600 mm,动平台边长为200 mm。约束移动副与转动副的活动范围,设定其移动位移及摆动角度:支链Ⅰ、Ⅱ、Ⅲ的初始长度为400 mm,最大伸长量是820 mm;其C副绕x轴转动的限制-60°～60°,R副绕y轴方向的转动限制为0°～90°。代入点的位置参数求出机构的运动学逆解,经由MATLAB计算进而选取机构所有符合条件的点位,点的集合即为所求工作范围。利用scatter函数绘制工作空间,得到图3所示的最后结果。

图3 2-CPR/RPU并联机构工作空间Fig.3 Workspace of 2-CPR/RPU parallel mechanism

分析图3可知,2-CPR/RPU并联机构没有奇异位置,在yOz平面内动平台绕x轴转动的角度最大为60°,内部连续无空洞,具有较大范围的工作空间。

6 工程有限元分析

当前物流产线上的货件形状各异、大小不一,且拣选方式仍依赖于人工调配,摆放位置无序杂乱,分拣效率低下。在实际分拣过程中,不规则形状的货件占比约1/2,多数货件的自然倾角在45°以内。提出的2-CPR/RPU并联机构,转动角度最大可至60°,能够满足不同规格货件的拣取。如图4所示,分拣机构在产线运行过程中,组合吸盘位于动平台中心位置,当货件随输送线运送至机构下方时,吸盘沿z轴下移并绕x轴转动至与货件倾面相平行处开始吸附,然后回升沿x轴移动到相接输送线上方,再次沿z轴下移并松压放置,完成分拣作业。

图4 并联机构持物分拣Fig.4 Parallel mechanism clamping cargo sorting

实际应用中,一般快件、包裹重量不超过20 kg,横向周长不超过1 500 mm。将机构模型导入ANSYS中并设定该机构材料为铝合金,添加静平台固定约束,动平台载荷为50 kg(490 N),分析得到该机构水平拣选时的应力应变,如图5所示;以及当其进行摆角拣选时的应力应变,如图6所示。

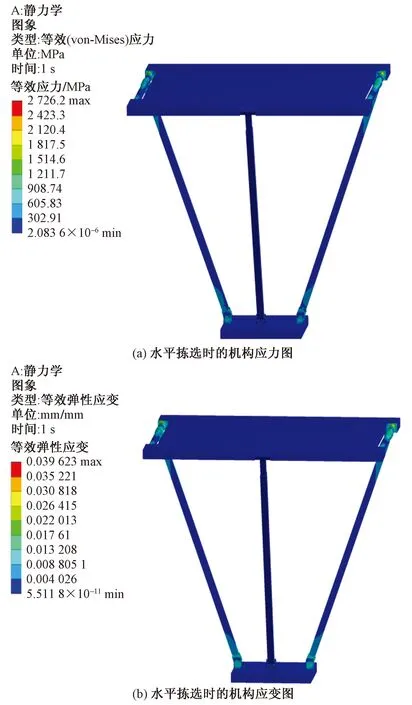
图5 机构水平载物分拣时的有限元分析Fig.5 Finite element analysis of mechanism horizontal load sorting

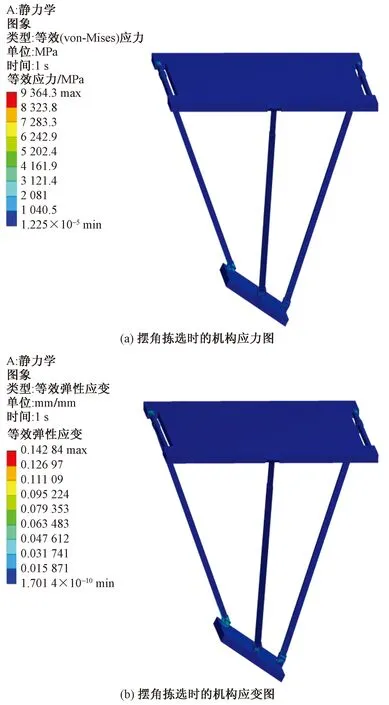
图6 机构摆角载物分拣时的有限元分析Fig.6 Finite element analysis of mechanism swing angle load sorting

综上可知,该机构承重性能良好,形变较小,可满足大多产品在预设范围内的分拣运输,提升配送传输质量,具有较好的实用性和可行性。

7 结论

(1)提出一种三自由度的并联机构2-CPR/RPU,建模且通过螺旋理论分析得知机构具有2T1R型的运动,即沿x、z轴方向上的移动以及绕x轴的转动,并根据修正的Grübler-Kutzbach公式验证。求解该机构的位置逆解表达式,进而推导其关节驱动输入与平台输出的速度关系。

(2)通过代数法分析奇异位形存在的条件,满足机构本身尺寸的情况下表明机构运行过程中并不存在奇异性,运动性能良好。数值搜索法分析该机构的工作空间,观察结果得出机构工作范围和转角较大,工作空间内部连续无空洞。

(3)结合物流分拣实例,通过有限元分析可以得到机构载物分拣过程中形变范围较小、承重能力较高、结构稳定性较好。该机构在实际作业中可替代人工在多数物流包装领域进行拣选工作。