基于机器学习与视觉的四足机器人步态精确监测方法

秦鹏举, 蒋周翔, 苏瑞, 宋鹏成, 马紫怡

(北京信息科技大学机电工程学院, 北京 100192)

随着机器人仿生学的发展,四足机器人逐渐成为移动式机器人领域的研究热点。四足机器人凭借出色的运动性与环境适应性,被充分应用于军事、生活、娱乐等场景,具有较大的发展潜能[1]。代表性的四足仿生机器人有波士顿动力公司研发的BigDog和SpotMini[2],麻省理工学院研发的Cheetah猎豹机器人[3]以及山东大学研发的Scalf四足机器人[4]等。

四足机器人的步态直接影响其运动能力和稳定性。随着应用场景不断拓展,对机器人性能的需求也日益提高,其中就包括了要求机器人步态轨迹长期稳定保持高精度。然而,长期行进会导致关节和传动系统损耗,通过运动链的传播积累会显著影响足端位姿和步态轨迹精度[5]。解决方法中的关键一环就是如何对足端位姿进行精确监测。

在位姿测量领域,如激光跟踪仪、双球杆仪等在内的测量设备[6-7]通常以大体积工业机器人为对象,难以用于移动轻巧的足式机器人。相比之下,机器视觉不仅成本低廉,而且便捷快速,在机器人位姿测量中得到了广泛的应用。Balanji等[8]提出了一种基于单目视觉的机器人运动学标定方法。Fu等[9]通过固连在机器人末端的棋盘格标记用于辨识其运动学参数。Wang等[10]基于单目视觉和ChArUco(chess augmented reality university of cordoba)标记对六足机器人进行了位姿测量。这些方法的数据来源均为相机所拍图像,因此易受镜头畸变、光照差异、相机标定等因素影响,导致位姿测量精度不足。

面对上述现状,以四足机器人的Trot步态(对角小跑步态)轨迹为对象,依据轨迹规划结果选取步态监测点。采用双目相机实时观测足端靶标位姿,并基于机器学习方法将“不精确”位姿测量结果修正为足端“精确”步态位姿数据,从而实现精确步态监测。

1 系统设计

将双目相机安装在四足机器人前端,其视场范围应包含两个前足的完整步态轨迹,识别靶标采用ArUco[11](augmented reality university of cordoba)标记并安装在机器人足端,如图1所示。在还未长期运动而产生积累误差时,建立足端名义运动学模型并计算足端“精确”的名义位姿,同时视觉采集获得靶标“不精确”的测量位姿。以此构建深度神经网络建立二者映射关系,即可通过实时观测步态监测点处靶标位姿,准确预测足端位姿,以保证足端轨迹精度和步态运动周期性。

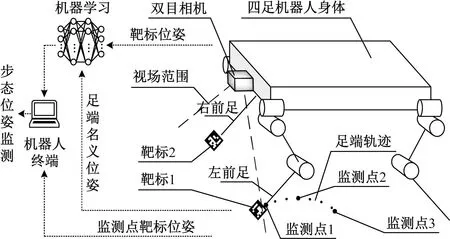
图1 监测系统整体示意图Fig.1 Schematic diagram of monitoring system

2 步态监测点选取

2.1 步态特征分析

由于Trot步态相比其他步态在能效、速度变化范围、步态稳定性上均有明显优势,且应用最为广泛[4],因此选择Trot步态作为监测点选取对象,以保证监测方法具有广泛适用性。

一个完整的步态周期分为摆动相和支撑相,而摆动相决定了机器人跨步步长与抬腿高度。为保持步态运动稳定性与流畅性,防止产生冲击,摆动相足端落地与抬起瞬时速度应为0。因此四足机器人步态规划可定义为复合摆线轨迹[12]

(1)

(2)

2.2 步态监测点选取

将复合摆线轨迹分解为沿x轴及沿z轴方向的运动,如图2、图3所示,分别为摆动相足端位置和速度变化曲线。

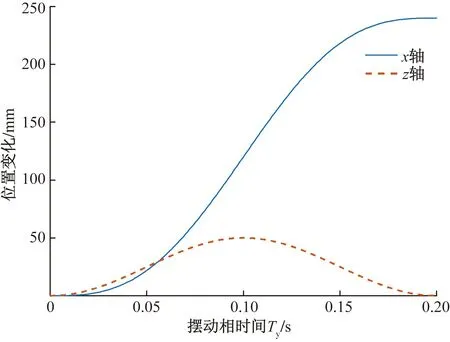
图2 摆动相足端位置变化曲线Fig.2 Swing phase foot position variation curve

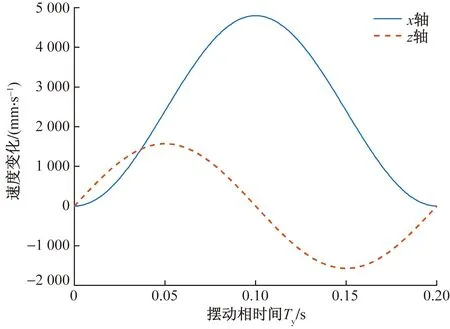
图3 摆动相足端速度变化曲线Fig.3 Swing phase foot end velocity variation curve

观察其运动特性可知,摆动相抬腿速度和落地速度均为0。在摆动足达到最高点时,z轴速度为0。因此选择监测点时依据步态位置稳定以及无冲击原则,以0T及0.5T为主要监测点,以0.25T为次要监测点。

3 步态位姿测量与计算

3.1 足端名义位姿计算

首先,基于D-H(Denavit-Hartenberg)参数法[13],建立四足机器人左前足运动学模型,定义基坐标系B位于机身中心,xB、yB、zB为基坐标系3个坐标轴,xi、yi、zi为左前足第i关节坐标系3个坐标轴,i=1,2,3;F为左前足末端坐标系,xF、yF、zF为左前足末端坐标系3个坐标轴;M为靶标坐标系,xM、yM、zM为靶标坐标系3个坐标轴;C为相机坐标系,xC、yC、zC为相机坐标系3个坐标轴。坐标系分布如图4所示。

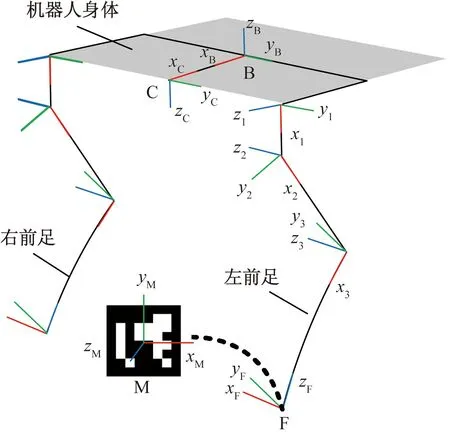
图4 坐标系分布Fig.4 Coordinate system distribution

足端名义位姿通过基坐标系描述,足端坐标系F相对基坐标系B的正运动学变换矩阵为

(3)

式(3)中:若将BT1看作0T1,3TF看作3T4,则i-1Ti表示第i-1关节坐标系到i关节的齐次变换矩阵,可表示为

i-1Ti=Rx(αi)Tx(ai)Rz(θi)Tz(di)

(4)

式(4)中:Rx(·)、Rz(·)为旋转矩阵;Tx(·)、Tz(·)为平移矩阵;αi、ai、θi、di为第i关节D-H参数[14]。

若将式(3)表征为

(5)

式(5)中:由nx、ny、nz、ox、oy、oz、ax、ay、az组成的旋转矩阵与px、py、pz组成的位置向量,用于表示齐次变换矩阵BTF。

为提升机器学习泛化能力,将BTF矩阵中各元素使用式(6)变换得到对应足端名义位姿向量PF,以此作为机器学习的标签进行有监督学习。其中,XF、YF、ZF为足端坐标系的位置坐标,θxF、θyF、θzF为足端坐标系绕基坐标系xB、yB、zB轴的旋转欧拉角,atan2(y,x)为双变量反正切函数。

(6)

3.2 足端靶标实际采集位姿计算

足端靶标实际采集位姿通过相机坐标系描述,相机到靶标坐标系实际变换矩阵为CTMa。为复现实际采集过程中视觉误差影响用于仿真验证,对CTMa进行如下变换。依据图4建立的D-H坐标系分布,相机到基坐标系变换矩阵恒为CTB,左前足端到靶标坐标系变换矩阵恒为FTM,因此相机到靶标坐标系理想变换矩阵CTM为

(7)

若将视觉系统复杂误差综合模型[14]表示为TMe,可得

CTMa=CTMTMe

(8)

采用与式(5)和式(6)类似变换,将CTMa转化为靶标实际位姿向量PMa=[XMa,YMa,ZMa,θxMa,θyMa,θzMa]T以此作为机器学习的特征进行有监督学习。其中,XMa、YMa、ZMa为相机坐标系下靶标坐标系的真实位置坐标,θxMa、θyMa、θzMa为靶标坐标系绕相机坐标系xC、yC、zC轴的旋转欧拉角。

4 神经网络设计

4.1 设计网络结构

深度前馈神经网络是目前机器学习与深度学习领域应用最广泛的模型,拟设计神经网络结构如图5所示。相邻节点使用全连接层搭建,采用ReLU激活函数进行修正,输出层采用线性激活函数,使该网络具有更加明显收敛性与稀疏性。

图5 神经网络结构Fig.5 Neural network architecture

隐藏层数和节点数直接关系着网络预测精度,对此,通常参考如式(9)所示经验公式来初定最佳隐层节点数L的范围[15]。

(9)

式(9)中:m、n为输入层以及输出层节点数;常数a=1,2,…,10。

由于输入和输出分别是实际采集足端靶标位姿向量和足端名义位姿向量,故令n=m=6,隐层节点数可选L=5,6,…,14。考虑到模拟相机采集足端靶标位姿时建立综合误差模型,引入多种干扰误差,因此在初选节点数14基础上进行调整,经过多次验证,隐层节点数为16,隐藏层数为3。

4.2 生成训练样本

依据第2节推论,以0T以及0.5T为主要监测点,以0.25T为次要监测点。将各点对应关节角度值代入式(3)、式(4)可得足端坐标系矩阵BTF。如图6所示,以每个步态监测点位置(px,py,pz)为中心,规划边长为100 mm的立方空间,在内部均匀取103个训练点。然后在±5°范围内均匀取10个值,生成103个不同的角度组合(δαF,δβF,δγF)。令足端坐标系BTF依次绕xF、yF、zF轴旋转δαF、δβF、δγF角度,得到103个训练点对应的足端坐标系位姿矩阵BTF。将BTF依次代入式(5)、式(6)求得训练点对应的足端名义位姿向量PF。然后综合式(5)～式(8)可计算出训练点对应足端靶标实际采集位姿向量PMa。将PMa作为神经网络输入特征,PF作为输出标签,由此训练所得神经网络可根据监测点临域内某点的足端靶标实际采集位姿预测出对应足端名义位姿。

5 仿真验证

5.1 步态监测点仿真验证

如表1所示,使用D-H参数在仿真软件中建立四足机器人左前足模型,使用正运动学公式[式(3)]解算足端位姿,使用蒙特卡洛法仿真出左前足的工作空间如图7所示。

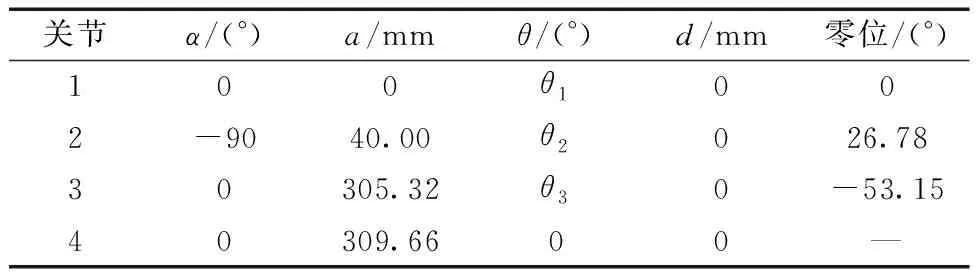
表1 四足机器人左前足D-H参数设置

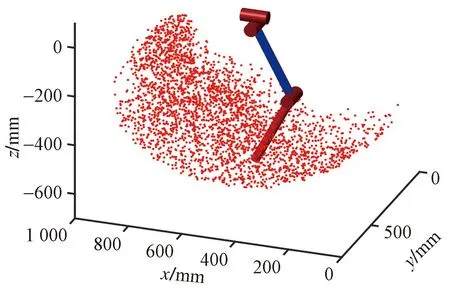
图7 左前足工作空间Fig.7 Front left foot workspace

如表2所示,将数据代入式(1)、式(2),使用复合摆线形式进行Trot步态轨迹规划后,利用反变换逆解算法[16]求出摆动腿各个旋转关节的角度值。再代入式(3)生成左前足摆动相足端轨迹。进而在摆动相足端轨迹中提取出3个步态监测点如图8所示,解算出各个步态监测点摆动腿各旋转关节角度值如表3所示。

表2 Trot步态规划参数设置

表3 步态监测点对应关节角度值

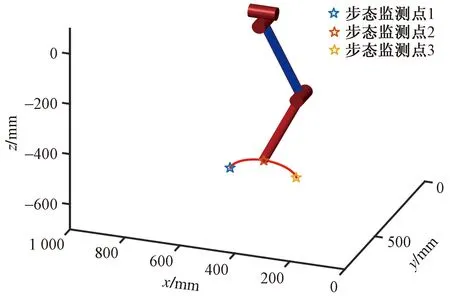
图8 步态监测点示意图Fig.8 Schematic diagram of gait monitoring points

仿真结果表明,经过Trot步态规划后的足端轨迹与复合摆线轨迹一致,观察监测点1处的足端位置,恰处于摆动相抬腿落地时刻,且速度为0。符合步态位置稳定以及无冲击原则,满足使用需求。

5.2 神经网络仿真验证

5.2.1 神经网络训练

神经网络仿真验证根据3种典型影响因素建立了靶标采集位姿综合复杂误差模型TMe,模拟采集环境影响,验证基于机器学习与视觉的四足机器人步态精确监测的准确性,仿真流程如图9所示。

图9 神经网络仿真流程图Fig.9 Neural network simulation flowchart

拟采用步态监测点1作为仿真验证对象,相较于其他监测点,其更靠近视场边界,受畸变以及光照影响相对明显,更加典型。依照4.2节训练样本的生成方法,使用表3中步态监测点1对应的关节角度值作为仿真验证的对象,求得邻域内足端名义位姿向量PF,再根据3.2节所分析综合误差带来的影响,依照仿真流程图,对足端靶标实际采集位姿进行仿真验证,首先依据真实情况,为相机到机器人基坐标系CTB与足端到靶标坐标系FTM赋值,如表4、表5所示。综合误差模型包含相机标定、相机畸变、光照差异3种典型影响因素,然后为综合误差模型TMe赋值,如表6所示。据此计算得到足端靶标实际采集位姿向量PMa。

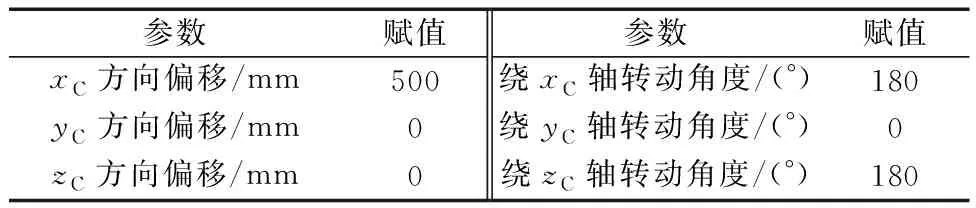
表4 相机到基坐标系的变换矩阵CTB赋值Table 4 Camera to base transformation matrix CTB assignment

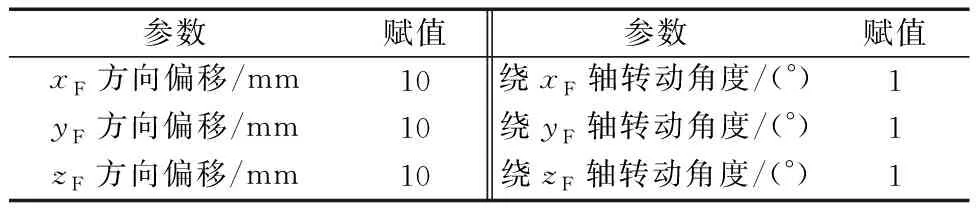
表5 足端到靶标坐标系变换矩阵FTM赋值Table 5 Foot to target transformation matrix FTM assignment

表6 综合误差模型TMe参数赋值Table 6 Integrated error model TMe parameter assignment

仿真生成监测点1邻域训练样本如图10所示。

红色点阵为靶标坐标;蓝色点阵为足端关节坐标

观察两组点阵之间存在一定程度的差异,说明训练样本融合了靶标安装偏置、光照差异以及视觉系统导致的测量误差。随后将靶标采集位姿向量PMa作为模型特征输入,足端名义位姿向量PF作为模型标签输出,经过归一化特征处理,取训练样本中的900个目标点作为训练集,其余100个目标点作为验证集。其中模型最大训练次数为2 000,学习率为0.01,训练目标最小误差为10-6。采用4.1节所搭建的模型结构,网络训练结果如图11所示。在步态监测点1处的网络训练结果均方误差可达到1.7×10-5,可见神经网络能够准确地学习视觉系统误差到靶标位姿采集误差的映射关系。

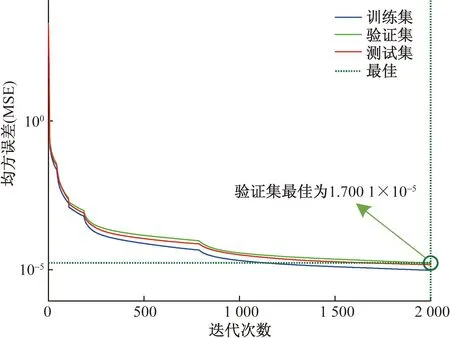
图11 神经网络训练结果Fig.11 Neural network training results

5.2.2 神经网络测试

在步态运行过程中,由误差积累导致的足端偏移范围较小,为模拟真实条件且验证神经网络的可信度,据此在步态监测点1较小邻域内随机生成更为密集、方位角范围更加离散的测试样本进行仿真测试。监测点1邻域的测试样本如图12所示。该点阵相较于训练样本更加复杂,因此步态监测精度效果验证更加可靠。

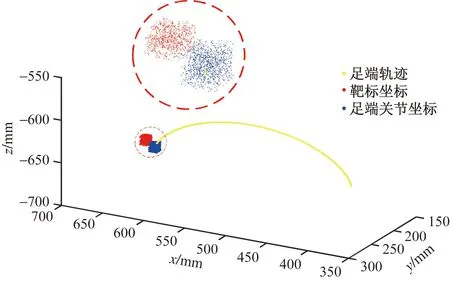
图12 测试样本点位分布Fig.12 Distribution of test sample points

5.2.3 验证结果与分析

将测试样本中的足端靶标实际采集位姿向量PMa′输入步态监测点1训练后的网络中,得到足端名义位姿向量预测值PMap。在步态监测过程中,仅需要保证其位置精度,但该方法亦预测了其姿态。因此主要对足端位置预测精度进行验证。将预测值PMap位置坐标与测试样本足端名义位姿向量PF′位置坐标进行解算,求得预测点位与真实点位之间的距离误差如图13所示。数据点越蓝表明距离误差越小,观察可知,面对更加密集、复杂的测试点集,相机采集靶标位姿的预测点位置与真实足端位置误差均处于亚毫米级别,最大点位距离误差不超过0.05 mm。

图13 预测点与真实点之间距离误差Fig.13 Distance error between predicted and actual point

为更加详细的评价监测精度,随机抽取100个测试样本在步态监测点1处的预测点位与真实点位误差如图14所示,可以看出,预测误差集中分布在0～0.01 mm范围内,最大预测误差不超过0.03 mm。

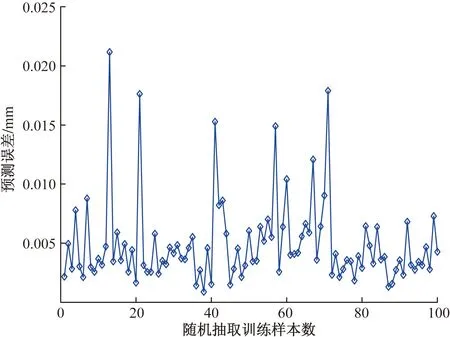
图14 随机样本预测误差Fig.14 Random sample prediction error

所有测试样本在步态监测点1处的预测点位与真实点位误差分布直方图如图15所示,仿真结果表明,监测精度误差平均值达到0.006 mm,最大值仅为0.057 mm,在超过99.68%的测试样本中,相机拍摄靶标的复杂误差数据,经过神经网络训练后对足端位置预测精度能达到0.025 mm。因此该方法可以满足对机器人足端位姿预测精度的需求,能够完成对步态轨迹的实时监测,保证其完成精确的步态运动。

图15 预测误差分布直方图Fig.15 Histogram of prediction error distribution

6 结论

针对四足机器人步态运动精度问题,使用了机器视觉方法进行步态监测,提出引入机器学习的方法对视觉系统测量误差进行学习修正,以相机采集靶标位姿预测足端真实位姿。仿真结果表明,新方法具有较高的预测精度,能满足步态实时高精度监测的需求,进而为足式机器人实现精确的足端定位以及保持步态周期性提供了理论依据和技术支撑。

由于实际的视觉采集过程还存在一些其他因素干扰,因此下一步研究计划是搭建实验平台验证新方法在现实场景下的测量精度,以针对该方法的实际应用做进一步优化与完善。