基于FNN与表现评价模型的生物教学研究

黄胜威

(安徽科技学院 生命与健康科学学院，安徽 滁州 233100)

模糊神经网络(Fuzzy Neural Network，FNN)是一种基于模糊逻辑的人工神经网络模型，具有模糊推理能力和学习能力。它可以通过模糊规则和输入输出数据训练，实现对复杂问题的建模和求解。在生物课堂教学中，利用模糊神经网络可以对学生的学习情况进行评估和预测。表现型评价模型是一种基于学生实际表现的评价方法，通过对学生的行为和动作进行观察和记录，评价学生的学习效果和能力水平。在教学中，利用表现型评价模型客观地评估学生的实际掌握情况，为教师提供准确的反馈信息，帮助教师调整教学策略[1]。

1 融合表现型评价与模糊神经网络的生物教学模型构建

1.1 基于表现型评价的生物课堂教学方法优化

生物教学是指传授生物学知识和概念的教育活动。它的目的是帮助学生理解生物学的基本原理、生命现象和生物系统的结构和功能。生物教学通过课堂教学、实验、观察和研究等多种方式进行。它不仅培养学生对生物学的兴趣和理解，还培养学生的科学思维、观察和实验技能，以及解决生物学问题的能力[2]。学生在实验室或自然环境中进行实验和观察，通过亲自操作和观察现象来获取生物学知识。如学生可以进行植物的生长观察、动物行为观察等，从中总结生物学规律和概念。通过学生的实操能够发现相应的生物学问题，学生在生物学问题的解决中发挥主动性和创造性，还需要运用所学的知识和技能，分析和解决现实生物问题。在解决问题的过程中，需要学生充分利用团队合作和交流，可以共同设计实验、讨论实验结果和解释观察到的现象，互相学习和提供反馈。对表现型评价的生物课堂教学方法优化操作有：激发学生的学习兴趣，通过实际操作和观察，学生可以亲身体验生物学的奥妙，增加对生物学的兴趣，提高学习的主动性和积极性；培养学生的实践能力，通过实验、观察和问题解决，学生可以锻炼实际操作和实践能力，提高科学思维和解决问题的能力；加强学生的团队合作和交流能力，通过小组合作和班级讨论，学生可以相互交流和学习，培养团队合作和交流能力，提高学习效果；提高教学的针对性和个性化，基于表现型评价可以更全面地了解学生的实际能力和表现，教师可以根据学生的不同特点和需求，提供有针对性的教学措施和指导[3]。详见图1所示。

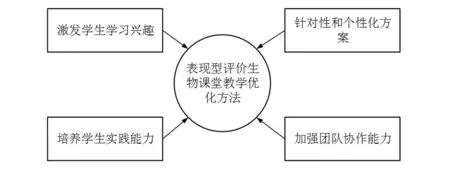
图1 基于表现型评价的生物课堂优化流程图

将表现型评价应用到生物课堂教学中，能够在现有教学课标的要求的基础上，对生物学科课堂上学生的表现评价的内涵进一步丰富和具体化。可见，表现型评价是教师通过模拟或真实的情境，让学生完成特定的任务，如小组讨论、实验、提问等，然后观察和分析学生在任务中的表现，根据学业质量标准制定评价标准，对学生的思维方法、探究能力和态度责任进行评价。通过评价，教师可以改进自己的教学方法，促进学生生物学学科核心素养的发展。

1.2 基于表现型评价与模糊神经网络的生物课堂教学模型构建

在表现型评价中，很多评价数据都是建立在经验知识基础上的，这种经验知识很多时候存在主观性。为了解决主观性的问题，研究引入了带有学习机制的模糊神经网络。为了减少主观性，可以引入学习机制对模糊系统进行修改和完善[4]。将模糊集合论中的模糊逻辑与神经网络的学习能力相结合，以更好地处理模糊、不确定和模糊边界的问题。结合表现型评价的模糊神经网络的设计步骤为：数据准备、创建模糊集合、设计模糊规则并推理、聚合结合并分析，根据输入和规则进行模糊推理，最后设计网络权值的学习算法，通过调整权值来优化网络性能。模糊神经网络的结构见图2。

通过模糊神经网络预测学生的学习情况，可以为教师提供科学的决策依据，帮助教师制定个性化的教学策略[5]。在生物课堂教学中，研究将表现型评价与模糊神经网络相结合，构建生物课堂教学模型。模糊神经网络是由输入层、模糊化层、模糊推理层和输出层构成的。在输入层中，节点与输入层是相连的，每个节点的输入公式可用公式(1)计算。

f1(i)=[x1，x2]，

式(1)

公式(1)中，x1，x2分别表示两个输入数据的值。为了进行模糊化，需要对利用高斯隶属函数进行模糊化操作，此时对高斯型隶属函数进行模糊化，该函数可用公式(2)表示。

式(2)

公式(2)中，cij表示第i输入变量在对应的第j个模糊集合隶属函数中的中心位置的数值；bj表示第i输入变量在对应的第j个模糊集合隶属函数中的宽度值。模糊化的目的是有效地映射输入值，需要根据网络输入值的范围设计隶属函数的参数。模糊化的目的是在有效地映射输入值的基础上，将输入值转化为模糊集合的隶属度。为了实现这一目标，需要根据网络输入值的范围来设计隶属函数的参数。隶属函数的参数包括模糊集合的形状、宽度和中心等属性，这些参数的选择对于模糊化的效果至关重要。通过合理地选择这些参数，可以确保输入值在模糊集合中得到准确的隶属度。模糊推理层通过与模糊化层的连接来匹配模糊规则，各个节点之间通过模糊与运算进行组合，从而得到相应的输出。对应模糊的规则输出可用公式(3)表示。

f3(l)=f2(1，j1)f2(2，j2)，

式(3)

公式(3)中，j1，j2的取值范围为[1，5]；l的取值范围为[1，25]。通过对应的模糊操作后，再对输出值进行加权操作，此时输出层的值可用公式(4)表示。

式(4)

公式(4)中，ω表示第四层输出与上一层各节点之间的连接矩阵对应值。在进行下一次迭代的过程中，重复权值的更新过程，直到满足预先设定的误差性能指标的要求为止。这种逐个样本的训练方式可以确保每个样本都得到充分的学习和更新，使得神经网络逐渐趋向理想的性能。通过不断迭代和调整权值，网络的性能逐渐提升，最终达到满足性能指标的要求。这种迭代训练的过程是神经网络学习和优化的关键步骤之一。结合上述研究，融合表现型评价与模糊神经网络的流程见图3。

图3 结合表现型评价与模糊神经网络的流程图

2 融合表现型评价与模糊神经网络的生物教学模型性能分析

研究通过对1032名在校学生和10名授课老师在生物课堂教学中的授课方式、学生学习情况等进行分析，获得了15组测试样本，23组验证样本。为了验证课堂教学模型的预测能力和样本数据检测能力，研究利用循环神经网络(Recurrent Neural Network，RNN)和图神经网络(Graph Neural Networks，GNN)与模型方法进行对比，通过对比三种算法的检测率、召回率、F1值和损失值来判断模型方法的性能。图4表示三种算法在相同数据集下的检测率和召回率的对比结果。

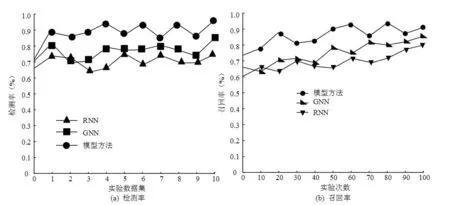
图4 三种方法的检测率和训练误差率对比

见图4(a)，模型方法的检测率最大值为97.26%，GNN的检测率最大值为84.33%，RNN的检测率最大值为73.92%。模型方法的检测率平均值为91.21%，GNN的检测率平均值为78.34%，RNN的检测率平均值为71.37%。由图4(b)可知，模型方法的召回率最高，平均值为90.53%，GNN的召回率平均值为82.41%，RNN的误差率平均值为73.83%；三种方法相比，模型算法比GNN和RNN的召回率平均值高8.12%、16.7%。这说明模型方法在数据集中的检测率和召回率均为最高。三种算法在训练集训练后的损失值和F1值对比结果如图5所示。

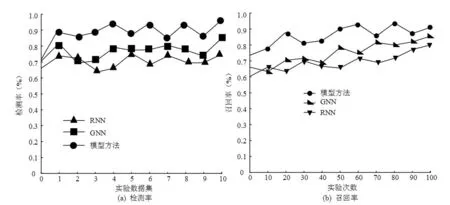
图5 三种方法的损失值和F1值对比结果

见图5(a)，三种方法的损失值随着迭代次数的增加都在降低，其中模型方法的损失值在迭代次数为206时基本没有出现波动，表明此时训练值已趋于稳定。GNN的损失值在迭代次数为367时趋于平稳，而RNN在迭代次数为583时才趋于稳定。见图5(b)，模型方法的F1平均值最高，模型方法的F1平均值为0.91，GNN和RNN的F1平均值分别为0.82和0.71，模型方法明显高于GNN和RNN的F1平均值。这说明从训练损失值和F1值来看，模型方法的性能优于GNN和RNN。验证了研究构建模型在生物课堂教学中的数据提取、分析的能力。为了验证模型预测成绩的实际应用效果，研究通过一段时间生物课堂教学后对某班的20名学生成绩进行分析和预测，同时也通过学生对该教学模型的满意度进行打分来判断构建模型的实际效果。真实成绩与预测成绩之间的误差代表了预测模型的准确度或误差程度。可以用于评估模型的性能和判断模型的可靠性。成绩预测和满意度评价结果见表1。

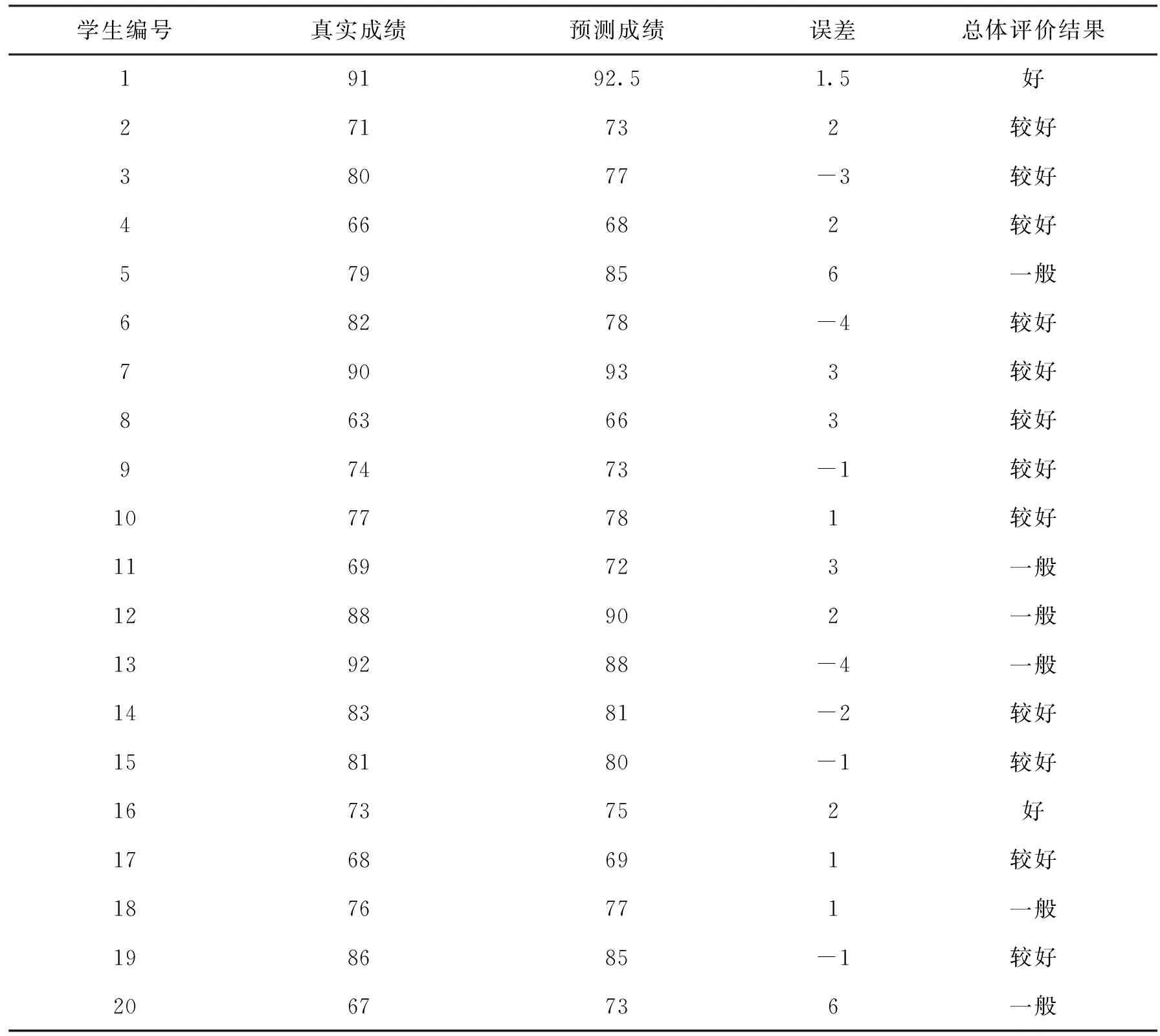
表1 预测成绩与真实成绩以及满意度对比结果

见表1，真实成绩与预测成绩之间的误差最大值为6分，其中误差可以分为正误差和负误差，可以推断误差是呈正态分布的，这进一步证明了模型的可靠性。同时，从学生的满意度评价中可以看出，大多数同学对生物课堂教学是满意的，只有少数同学觉得教学效果一般。这种差异可能与预测成绩的误差超过他们的心理预期有关。据此推测，对于那些预测成绩误差超过心理预期的同学来说，他们对教学效果的评价可能会受到一定的影响。通过表1的数据验证了生物课堂教学模型的可信性和稳定性。这意味着该模型在预测学生成绩方面是可靠的，能够为教师和学生提供准确的参考。同时，仍然需要关注那些对预测成绩误差较为敏感的学生。教师可以与这些学生进行沟通，帮助他们找到适合自身学习的方式，并鼓励他们根据实际情况进行努力，从而进一步提升整体教学效果。

3 结论

通过观察学生的行为和反应，教师可以及时调整教学策略和方法，然后引入模糊神经网络的理论，通过建立模糊神经网络模型来分析和预测学生的学习过程。通过模糊神经网络模型，教师可以更好地理解学生的学习特点和学习需求，从而更好地调整教学内容和方法。最后利用实验来验证构建模型的性能和实际应用效果。结果表明，模型方法的检测率平均值为91.21%，比GNN和RNN的召回率平均值高8.12%、16.7%，误差在迭代次数为206时基本没有出现波动，迭代次数也明显低于对比方法，同时从预测成绩与真实成绩的对比可知，大多数同学对构建的生物课堂教学模型是满意的。但研究还存在不足之处，该模型的数据采集具有局限性，在以后研究中需进一步完善数据的采集和整理工作，提高其适用性，将其应用于其他学科的教学中。