壳体柔性对风电齿轮箱-发电机集成系统动态特性影响

陈锐博 秦大同 刘长钊

收稿日期：2022-04-28

网络出版日期：2022-09-22

基金项目：国家重点研发计划资助项目（2018YFB2001601）。

作者简介：陈锐博 （1993—），男，博士研究生，主要从事风电传动系统机电集成设计研究，（E-mail） chenruibo@cqu.edu.cn。

通信作者：秦大同，男，教授，（E-mail） dtqin@cqu.edu.cn。

摘要：针对风电传动系统集成化结构，提出了一种可用于风力发电机变速-变载工况下的机电-刚柔耦合动力学模型，不仅考虑了齿轮的时变啮合刚度、相位关系、轴和壳体的结构柔性等机械因素，同时计入了发电机系统中永磁体磁饱和特性、电磁径向力波以及空间谐波等电磁因素。探究齿轮箱-发电机集成系统机电耦合动态特性，讨论了壳体柔性对系统动态特性的影响，提出了一种升速分析法，找寻了系统的共振转速。结合模态能量法和阵型矢量分布原理，找寻了共振时的潜在危险构件。研究表明：齿轮系统与发电机存在强耦合特性，壳体的柔性对系统机电耦合特性影响显著。针对集成化系统而言，齿轮内激励为共振转速下的主要激励源；但采用薄壁壳体时，发电机电磁激励不容忽视，易激发新的共振转速。选择合理的壁厚可有效提高系统的安全可靠性，减少共振区域，减轻系统构件的损坏。

关键词：风力发电机；电磁激励；啮合刚度；机电耦合；共振甄别

中图分类号：TH11          文献标志码：A             文章编号：1000-582X（2024）03-120-12

风能作为一种绿色可再生能源，具有环境友好、总储量大的优点，各国均在大力发展风电产业。风力发电机传动系统是实现风力发电的关键构件，因此，为了提高风电系统功率密度和发电量，风电传动系统也在向着轻量化和大型化的方向发展，但也给传动系统的设计研究带来了诸多挑战，尤其是针对齿轮-发电机集成系统的轻量化设计而言，单纯以齿轮或者发电机系统为研究对象已无法满足风电齿轮-发电机集成系统的设计要求。

传统的风电齿轮系统的设计研究中，文献[1-3]报道了风电齿轮系统的内部激励和运行工况对动态特性的影响。文献[4-6]报道了系统的构型、重力以及销轴选择等结构特性对动态特性的影响。针对风机传动系统的安装方式，文献[7-10]报道了塔架的晃动、俯仰角以及叶片柔性等对齿轮系统动态特性的影响。随着风电齿轮传动系统的轻量化要求，越来越多的齿轮箱采用了薄壁壳体，空心轴等柔性构件，因此，也有很多学者针对齿轮-箱体-转子的刚柔耦合进行了研究。Helsen等^[11]用SIMPACK建立了不同复杂度的风电齿轮箱模型，研究了行星架/内齿圈的结构模态与齿轮箱的结构模态之间的相互影响。Jin等^[12]基于SIMPACK建立了5 MW风电齿轮箱多体动力学模型，对比了不同结构柔性对系统模态和动态特性的影响。Li等^[13]建立了风电齿轮传动系统全自由度柔性动力学模型，研究了不同激励下的传动系统动力学特性。上述文献单纯报道了齿轮系统在内、外部激励下的刚-柔耦合动态特性，缺少全面针对风电齿轮-发电机传动系统的机电-刚柔耦合特性的研究。对于风电齿轮-发电机-壳体集成化传动系统而言，发电机-齿轮-壳体之间存在着多场耦合，其中包含了齿轮的内激励、发电机的电磁激励以及两者产生的耦合激励形式，其耦合作用机理更为复杂多样。

对电动机-齿轮系统的研究在不断地深入，其中以采煤机、电动汽车等领域取得的进展尤为显著。陈星^[14]、于蓬等^[15]建立了包含齿轮系统、电动机及其控制系统机电耦合动力学模型，分析了系统的振动特性，并通过对谐波电流的优化减小了传动系统的扭转振动。Yi等^[16]、Liu等^[17]和Bai等^[18]均建立了采煤机截割部电机驱动多级齿轮传动系统的机电耦合模型，研究了电机磁场、运行速度和加速度等因素对截割传动系统固有振动特性的影响，以及采煤机在稳态、负载突变、电压突变等工况下的动态响应。当前大多数研究为电动机-齿轮系统的机电耦合作用，与风力发电机齿轮-发电机传动系统机电耦合动态特性存在差异。

笔者以风力发电机传动系统齿轮箱-发电机集成化系统为研究对象，在考虑齿轮系统的内激励特性、发电机系统的电磁激励特性以及壳体、空心轴的柔性等非线性因素的基础上，提出一种可用于风力发电机变速-变载工况下的机电-刚柔耦合动力学模型，探讨了壳体壁厚对齿轮系统动态激励、振动特性以及发电机动态特性和电信号的影响，提出一种共振转速预测方法和一种潜在危险构件的甄别方法，为实现风力发电机齿轮-发电机系统集成设计提供了理论依据。

1風力发电机传动齿轮箱-发电机系统机电-刚柔耦合模型

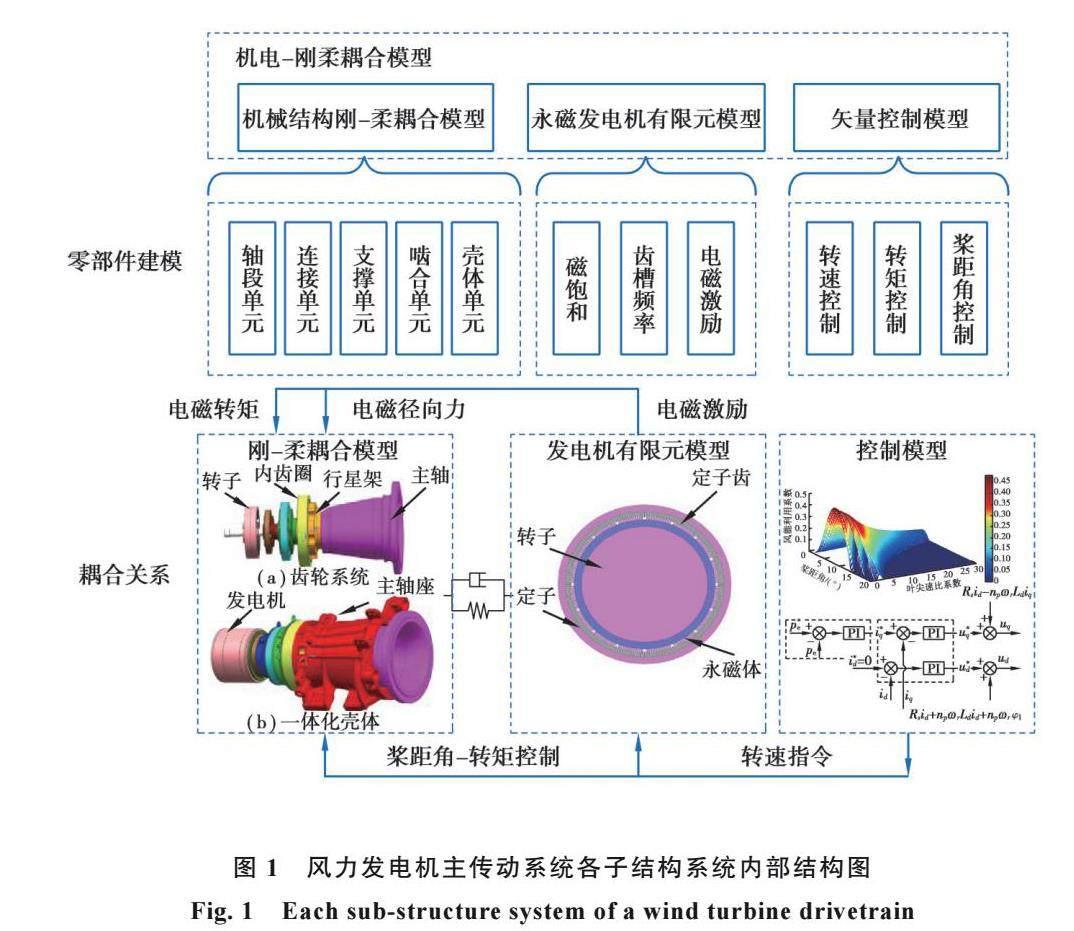
以8 MW风力发电机齿轮箱-发电机集成化传动系统为研究对象，建立系统的机电-刚柔耦合模型。该模型主要包含机械系统的刚柔耦合模型、发电机系统有限元模型以及矢量控制模型，如图1所示。其中：P_e为发电机运行过程中实际输出功率；P_e^*为给定期望发电机功率；i_d^*为d轴电流期望值；i_q^*为q轴电流期望值。齿轮系统的各级基础参数如表1所示。

1.1风电传动系统刚-柔耦合模型

齿轮-发电机-箱体系统刚柔耦合动力学模型主要分为：轴段单元、连接和轴承支撑单元、啮合单元、壳体单元。根据构件的装配关系，将各个子模型进行耦合，最终形成齿轮-发电机-壳体的刚-柔耦合模型。

1.1.1 轴段、连接及支撑单元

齿轮轴、主轴的截面为空心圆柱形，采用Timoshenko梁单元建立其有限元模型。Timoshenko梁单元的质量矩阵、刚度矩阵以及组装方式见参考文献[19]。各级系统间通过花键连接，内、外花键结构等效为轴段单元，系统支撑单元为轴承，具体建模见参考文献[19]。

1.1.2 啮合单元

根据行星轮系传动结构特点，在行星架转动坐标系中建立动力学模型。行星齿轮平移-扭转动力学模型如图2所示。不考虑齿轮的扭摆振动，建立如下3个坐标系：OXYZ为行星轮系静坐标系；行星架随动坐标系Oxyz的x轴通过第一个行星轮的理论中心；行星架随动坐标系O_nx_pny_pnz_pn的O_n位于第n個行星轮的理论中心，（n=1，2，…，N；N为行星轮个数），其x_pn、y_pn、z_pn坐标轴与坐标系Oxyz的3坐标轴分别平行。图2中，s、pn、r、c分别表示太阳轮、第n个行星轮、齿圈和行星架。θ_j（j=s， r， c， pn）是中心构件的转角，在坐标系OXYZ中度量；θ_pn是行星轮n的扭转角位移，在坐标系O_nx_pny_pnz_pn中度量。k_bxj、k_byj和k_bzj分别代表各个部件的支撑刚度；c_bxj、c_byj和c_bzj分别代表各个部件的支撑阻尼，k_rt和c_rt分别为齿圈的扭转支承刚度和扭转支承阻尼；k_spn和k_rpn分别代表外啮合和内啮合刚度；c_spn和c_rpn分别代表外啮合和内啮合阻尼；ψ_n是行星轮n沿行星架周向分布的位置角，；r_c为为行星架销轴位置距离行星架中心节点的距离；T_s、T_c分别为系统的负载转矩和驱动转矩。具体的建模方法见参考文献[20]。该建模的主要特点为系统转速、齿轮啮合刚度的波动频率由外部控制系统及外界载荷决定，系统各构件的转动均采用扭转角位移，而非传统的振动位移。因此，该建模方法更适用于变速、变载运行工况下的齿轮传动系统。

分别设由太阳轮向行星轮的指向为啮合线的正方向，行星轮向内齿圈的指向为啮合线的正方向，可得到行星轮系内、外啮合的齿面啮合变形δ_rpn和δ_spn，可分别表示为

1.1.3 壳体缩聚单元

模型缩聚法是一种将原模型全节点自由度通过数学算法转化到主节点自由度，消除模型中的副自由度，由少数自由度表示全自由度的动力学结构特性的方法。本系统壳体主要由主轴座、中间壳体、后壳体以及发电机的壳体组成，其装配关系如图3所示。图3中：Lsh1、Lsh2、Lc1、Mc1、Mc2、Hc1、Hc2、R1、R2、O₁₅～O₃₀分别各子结构件的缩聚节点编号；K_bLsh1和K_bLsh2分别为主轴上风向、下风向轴承支撑刚度矩阵；K_bLc为低速级行星架轴承支撑刚度矩阵；K_bMc1和K_bMc2分别为中速级行星架上风向、下风向轴承支撑刚度矩阵；K_bHc1和K_bHc2分别为高速级行星架上风向、下风向轴承支撑刚度矩阵；K_bR1和K_bR2分别为发电机转子上风向、下风向轴承支撑刚度矩阵。

结合壳体的缩聚节点与各子单元的装配关系，建立齿轮-轴系-轴承-转子-壳体的刚柔耦合模型，系统耦合动力学方程为

1.2永磁同步发电机动力学模型

表2为永磁同步发电机结构与电气参数。采用有限元软件构建了永磁同步发电机有限元模型。本系统永磁同步发电机为表贴式结构，如图4（a）所示。由于电机的几何形状、空间谐波以及铁芯的磁饱和状态的影响，发电机的磁链φ₁和电感L_d、L_q均是随电流变化的变化量，呈现出非线性特性，如图4（b）所示，图中i_d和i_q分别为d、q轴电流。图4（c）中F_r为永磁电机电磁径向力。图4（d）中f_e为电机基波电频率。

利用麦克斯韦应力张量法求出定子铁心内表面单位面积上的径向电磁力和切向电磁力。由于发电机定子齿处所受电磁力位于定子齿的切向和径向，为了便于后续与箱体进行耦合，需经过坐标变换将其转换到直角坐标系中，如式（7）。圖4（c）（d）为空间电磁径向力的时域、频域图，径向力的频率成分主要为电频率的偶数倍谐波频率。

风力发电机的控制环节主要分为速度变桨控制以及发电机的转速、转矩控制环节。发电机转速转矩控制环节主要针对风力发电系统的变功率输出阶段，发电机转速指令由控制器给定。变桨控制根据风能利用系数以保证系统运行的安全性，详细内容见参考文献[20]。

1.3齿轮箱-发电机系统机电-刚柔耦合动力学模型

结合上述各子系统模型，建立了齿轮箱-发电机一体化传动系统的机电-刚柔耦合模型如式（9）所示：

依据上述数学模型，采用数值计算软件分别搭建三相永磁同步发电机和多级齿轮系统的数值仿真模型，结合矢量控制方法，将发电机转矩与转速作为齿轮与发电机间的实时变量进行耦合传递。本研究中忽略变频器的影响，仅分析在正弦波电压供电下的发电机的电磁特性。

2壳体柔性变形对齿轮-发电机系统耦合动态特性的影响

2.1额定工况下耦合系统动态特性

讨论风速为10.5 m/s、发电机转速为780 r/min的额定工况条件下，壳体柔性（即薄壁壳体与壳体壁厚扩大2倍后的刚性壳体）对机电-刚柔耦合系统动态特性的影响。如图5所示，高速级内啮合动态啮合力均值为223 kN，幅值变化为-120 N～439.5 kN，啮合过程中出现了齿面分离和齿背接触现象。从图5（a）中可以看出，壳体的柔性对系统动态啮合力幅值有影响，但影响较小。图5（b）为频域分布图，高速级动态啮合力中的频率成分复杂多样，不仅有高速级啮合频率（f_m3），同时也包含低速级（f_m1）、中速级的啮合频率（f_m2）以及发电机的电磁激励频率（4f_e、6f_e），因此，发电机系统与齿轮系统存在强耦合作用。当壳体壁厚增加，中速级啮合频率以及电磁激励频率成分所具有的能量增大，加强了级间的交互作用。

图6为发电机定子位置径向振动加速度的时、频域对比图。从图6（a）可以看出壳体壁厚对发电机振动加速度幅值影响显著，薄壁壳体下发电机定子处振动较大。结合图6（b）可知，发电机定子处的激励频率复杂多样，包含有发电机的电磁激励频率（4f_e、6f_e、8f_e），高速级、中速级齿轮系统啮合频率及其倍频，以及以齿轮啮合频率为载波频率、发电机电磁激励频率为调制频率的激励（f_m±4f_r）。其中齿轮系统的内激励对发电机定子的振动特性影响最大。齿轮系统为直齿轮，其啮合刚度变化剧烈，内激励特性明显，因此，在进行电机结构设计时，需考虑齿轮激励频率的影响。

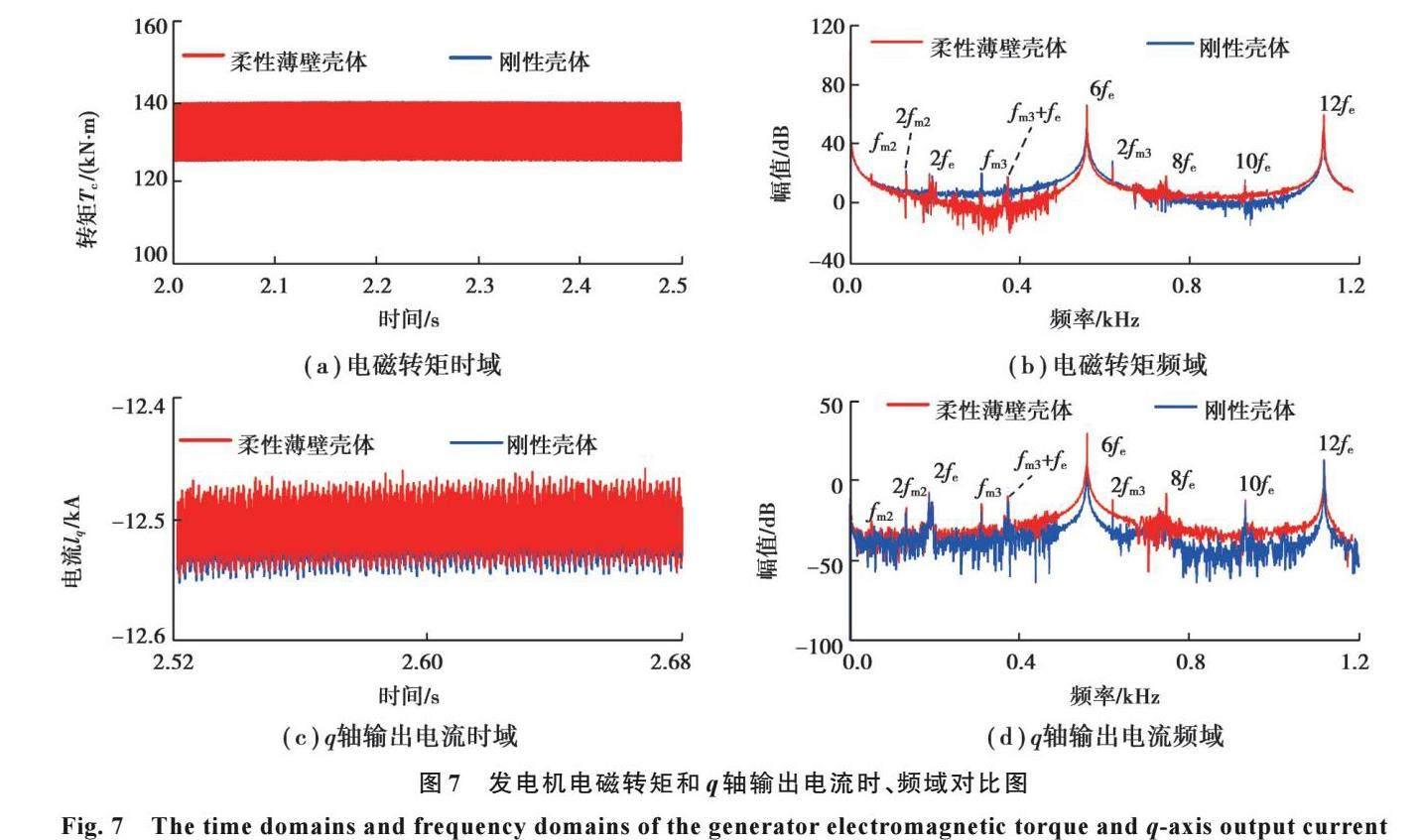
图7为发电机电磁转矩的时、频域对比图。壳体柔性对发电机电磁转矩影响较小，额定转速下发电机输出电磁转矩均值为132 kN·m。电磁转矩中的频率成分不仅包含电磁基波频率f_e的6倍、12倍、18倍等谐波频率，同时还包含了齿轮系统的内激励频率成分，其中以高速级啮合频率的2倍频（2f_m3）能量最大，其次为中速级啮合频率的2倍频能量（2f_m2）。因此，发电机电磁转矩不仅受到电磁激励的影响，同时也受到齿轮系统啮合频率的影响。图7（c）（d）为永磁同步发电机q轴电流时、频域对比图。q轴电流是通过输出相电流的Clarck变换所得，在额定状态下，系统的q轴电流保持平稳输出，均值保持在12.5 kA，波动幅度较小。从图7（d）可以看出q轴电流中包含了电磁激励频率6f_e和12f_e，齿轮系统的啮合频率成分，如f_m2、2f_m2、f_m3等，以及以齿轮高速级啮合频率f_m3为载波频率和电磁激励频率f_e为调制频率的频率成分f_m3+f_e。其主要频率成分与电磁转矩频率成分相同，这主要是由于风力发电机运行控制中i_sd=0的设定。电流信号中出现的齿轮频率成分以及含有齿轮频率下调制频率成分的现象，可用于齿轮系统的运行状态监测和故障诊断。

2.2壳体柔性对耦合系统共振响应影响

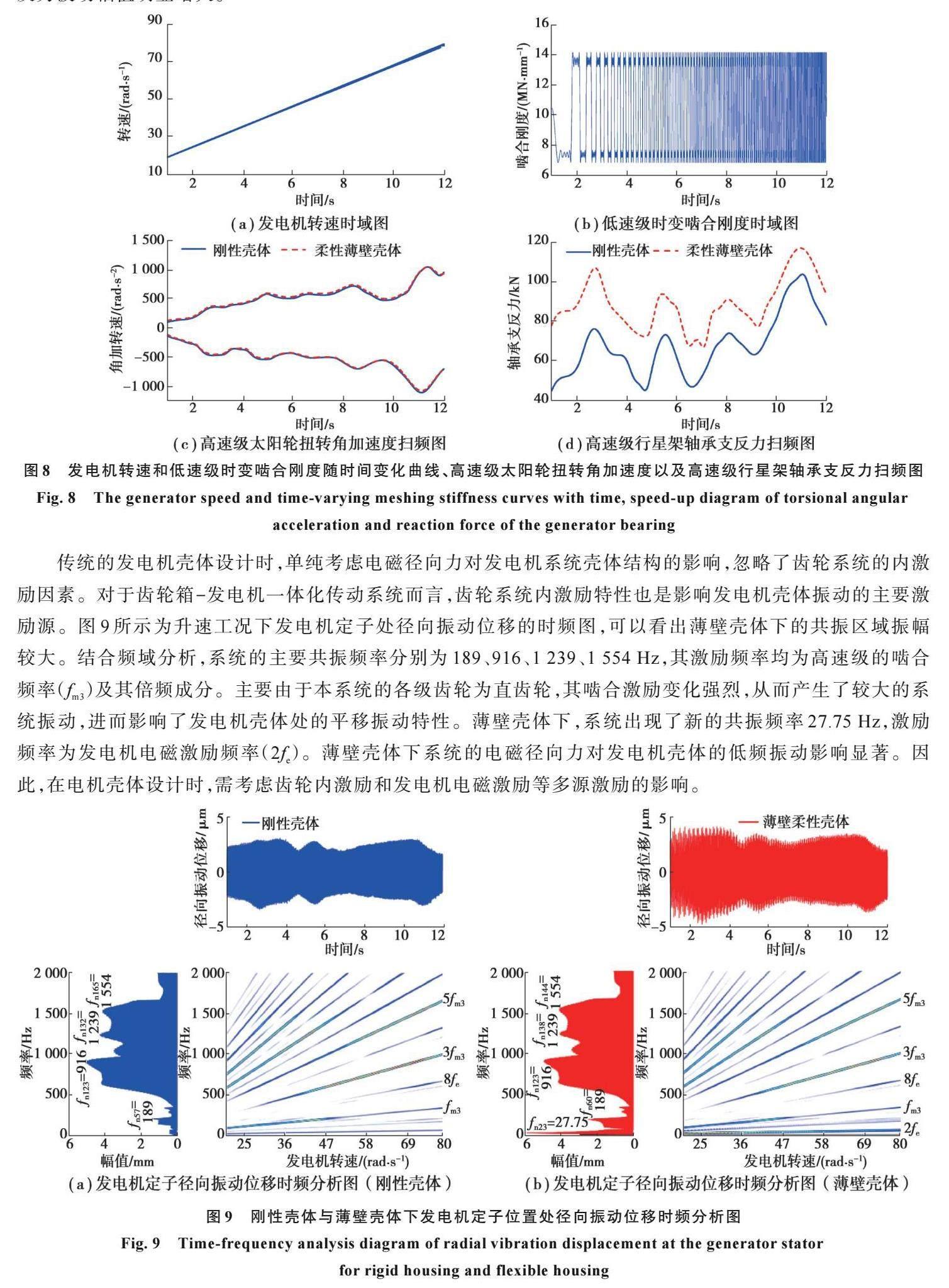
采用升速分析法，找寻风力发电机在运行过程中的潜在共振转速及危险构件。如图8（a）所示，发电机转速从启动转速20 rad/s提升到额定转速80 rad/s，历时11 s。图8（b）为低速级行星轮-内齿圈时变嚙合刚度随时间变化曲线，随着转速增加，齿轮啮合刚度变化速率增快。图8（c）（d）分别为高速级太阳轮扭转角加速度时域图的包络曲线以及发电机上风向位置处的轴承支反力波动幅值上包络曲线，可以看出，在工作转速范围内，系统出现了明显的共振区域，主要发生在发电机转速为29.0、40.7、60.0、75.0 rad/s。壳体柔性对太阳轮的扭转振动特性影响较小，对轴承支反力的影响较为显著。这是由于系统薄壁壳体下的形变更大，从而轴承支反力波动幅值明显增大。

传统的发电机壳体设计时，单纯考虑电磁径向力对发电机系统壳体结构的影响，忽略了齿轮系统的内激励因素。对于齿轮箱-发电机一体化传动系统而言，齿轮系统内激励特性也是影响发电机壳体振动的主要激励源。图9所示为升速工况下发电机定子处径向振动位移的时频图，可以看出薄壁壳体下的共振区域振幅较大。结合频域分析，系统的主要共振频率分别为189、916、1 239、1 554 Hz，其激励频率均为高速级的啮合频率（f_m3）及其倍频成分。主要由于本系统的各级齿轮为直齿轮，其啮合激励变化强烈，从而产生了较大的系统振动，进而影响了发电机壳体处的平移振动特性。薄壁壳体下，系统出现了新的共振频率27.75 Hz，激励频率为发电机电磁激励频率（2f_e）。薄壁壳体下系统的电磁径向力对发电机壳体的低频振动影响显著。因此，在电机壳体设计时，需考虑齿轮内激励和发电机电磁激励等多源激励的影响。

从图9可以看出，当发电机转速为75 rad/s，发电机定子径向振动出现了明显的峰值，判断发生了共振，共振频率为1 554 Hz，激励频率为高速级啮合频率的5倍频（5f_m3）。以该共振点为例，通过采用模态能量法和振型矢量分布原理^[20]，找寻了该系统共振频率下系统的危险构件。图10为第144阶模态下各刚性构件的模态应变能分布及振型矢量分布。k_asp与k_arp（a=L， M， H）分别为低、中和高速级的外啮合和内啮合刚度；k_bi（i=Lsh， Ls， Lr， Lc， Lp， Ms， Mr， Mc， Mp， Hs， Hr， Hc， Hp）分别表示从主轴到发电机转子处各个结构i的径向支撑刚度。如图10（a），薄壁壳体时，系统的模态应变能主要分布在高速级齿轮系统的啮合位置及内齿圈支撑位置。壳体壁厚增加后，系统的模态应变能发生了改变，高速级内齿圈-行星轮啮合位置处的模态应变能减小，太阳轮-行星轮啮合位置处和内齿圈支撑位置处的模态应变能增大。结合平移振动矢量分布图10（b）和扭转振动矢量分布图10（c），可以看出主要的振动构件为高速级太阳轮、内齿圈以及行星轮，随着壁厚增加，高速级系统平移与扭转振动能量减小。因此，选择合适的壁厚可有效改善系统的主要共振区域，增强构件的承载能力，避免破坏。

3结  论

针对风电传动系统复杂结构下的动态特性分析，提出了一种可适用于风力发电机的变速、变载特殊运行工况下的机电-刚柔耦合模型，综合考虑了齿轮传动的机械激励、发电机的电磁激励以及各结构件的柔性变形，首先研究了齿轮-发电机系统的机电耦合特性，进而讨论了壳体柔性对齿轮-发电机系统机电耦合特性的影响。结论如下：

1）齿轮系统与发电机系统存在多场耦合特性。发电机的电磁激励对齿轮系统的动态特性有显著影响，齿轮系统中的齿轮频率不仅会影响发电机系统的振动特性，同时会影响发电机的电磁转矩和输出电流的动态特性。基于电流信号中所出现的齿轮频率成分以及含有齿轮频率下调制频率成分的现象，可用于检测齿轮系统的运行特性和故障诊断。

2）改变壳体壁厚直接影响各级齿轮系统和发电机系统的强耦合特性，增大壁厚增强了电磁激励频率与啮合频率的交互作用。壁厚改变对齿轮-发电机系统各构件的扭转特性影响较小，但对各构件的平移振动特性影响显著。因此，在进行风力发电机齿轮-发电机集成结构设计的过程中，不可单独设计，要充分考虑齿轮激励特性和发电机激励特性的耦合作用机理。

3）采用升速分析法，结合模态能量分布和振型矢量分布原理，探究了系统的主要共振转速和潜在危险构件。对于多级直齿轮-发电机集成系统而言，齿轮系统的内激励频率为主要的共振激励源。采用薄壁壳体时，在发电机壳体位置处，系统出现了由电磁激励激发的新的共振区域。因此，在壳体壁厚设计时，需综合考虑发电机电磁激励和齿轮系统内激励特性对系统共振的影响。选取合理的壁厚，不仅有助于实现轻量化设计，而且有助于减少共振区域，降低危险构件破坏的风险。

参考文献

［1］  周志刚， 秦大同， 杨军， 等. 变载荷下风力发电机行星齿轮传动系统齿轮-轴承耦合动力学特性[J]. 重庆大学学报， 2012， 35（12）： 7-14.

Zhou Z G， Qin D T， Yang J， et al. Gear-bearing coupling dynamics characteristics of wind turbine planetary gear transmission system under variable load[J]. Journal of Chongqing University， 2012， 35（12）： 7-14.（in Chinese）

［2］  秦大同， 白温毓， 张福平. 制动工况下风电齿轮传动系统的动力学特性分析[J]. 太阳能学报， 2015， 36（2）： 305-312.

Qin D T， Bai W Y， Zhang F P. Dynamic characteristic analysis of gear transmission system of wind turbine during braking process[J]. Acta Energiae Solaris Sinica， 2015， 36（2）： 305-312.（in Chinese）

［3］  秦大同， 李超， 唐飛熊. 变风载下变速风力发电机传动系统动力学特性研究[J]. 太阳能学报， 2013， 34（2）： 186-195.

Qin D T， Li C， Tang F X. Study on dynamic characteristics of gear transmission system of variable speed wind generator under varying wind load[J]. Acta Energiae Solaris Sinica， 2013， 34（2）： 186-195. （in Chinese）

［4］  Zhu C C， Chen S， Liu H J， et al. Dynamic analysis of the drive train of a wind turbine based upon the measured load spectrum[J]. Journal of Mechanical Science and Technology， 2014， 28（6）： 2033-2040.

［5］  Guo Y， Keller J， Parker R G. Nonlinear dynamics and stability of wind turbine planetary gear sets under gravity effects[J]. European Journal of Mechanics-A/Solids， 2014， 47： 45-57.

［6］  Guo Y， Parker R G. Dynamic modeling and analysis of a spur planetary gear involving tooth wedging and bearing clearance nonlinearity[J]. European Journal of Mechanics-A/Solids， 2010， 29（6）： 1022-1033.

［7］  Qiu X H， Han Q K， Chu F L. Load-sharing characteristics of planetary gear transmission in horizontal axis wind turbines[J]. Mechanism and Machine Theory， 2015， 92： 391-406.

［8］  Bejger A， Frank E， Bartoszko P. Failure analysis of wind turbine planetary gear[J]. Energies， 2021， 14（20）： 6768.

［9］  Li Z W， Wen B R， Peng Z K， et al. Dynamic modeling and analysis of wind turbine drivetrain considering the effects of non-torque loads[J]. Applied Mathematical Modelling， 2020， 83： 146-168.

［10］  Li Z W， Wen B R， Dong X J， et al. Aerodynamic and aeroelastic characteristics of flexible wind turbine blades under periodic unsteady inflows[J]. Journal of Wind Engineering and Industrial Aerodynamics， 2020， 197： 104057.

［11］  Helsen J， Vanhollebeke F， Marrant B， et al. Multibody modelling of varying complexity for modal behaviour analysis of wind turbine gearboxes[J]. Renewable Energy， 2011， 36（11）： 3098-3113.

［12］  Jin X， Li L， Ju W B， et al. Multibody modeling of varying complexity for dynamic analysis of large-scale wind turbines[J]. Renewable Energy， 2016， 90： 336-351.

［13］  Li Z W， Wen B R， Wei K X， et al. Flexible dynamic modeling and analysis of drive train for offshore floating wind turbine[J]. Renewable Energy， 2020， 145： 1292-1305.

［14］  陈星. 车用机电复合传动系统机电耦合非线性振动研究[D]. 北京： 北京理工大学， 2015.

Chen X. Study on electromechanical coupling nonlinear vibration of electromechanical transmission system for HEV[D]. Beijing： Beijing Institute of Technology， 2015. （in Chinese）

［15］  于蓬， 王珮琪， 章桐， 等. 电动车动力传动系机电耦合扭转振动分析与控制[J]. 振动与冲击， 2017， 36（17）： 10-15， 34.

Yu P， Wang P Q， Zhang T， et al. Electro-mechanical coupled torsion vibration analysis and control of electric vehicle drivelines[J]. Journal of Vibration and Shock， 2017， 36（17）： 10-15， 34. （in Chinese）

［16］  Yi Y Y， Qin D T， Liu C Z. Investigation of electromechanical coupling vibration characteristics of an electric drive multistage gear system[J]. Mechanism and Machine Theory， 2018， 121： 446-459.

［17］  Liu C Z， Qin D T， Lim T C， et al. Dynamic characteristics of the herringbone planetary gear set during the variable speed process[J]. Journal of Sound and Vibration， 2014， 333（24）： 6498-6515.

［18］  Bai W Y， Qin D T， Wang Y W， et al. Dynamic characteristics of motor-gear system under load saltations and voltage transients[J]. Mechanical Systems and Signal Processing， 2018， 100： 1-16.

［19］  Duan T T， Wei J， Zhang A Q， et al. Transmission error investigation of gearbox using rigid-flexible coupling dynamic model： theoretical analysis and experiments[J]. Mechanism and Machine Theory， 2021， 157： 104213.

［20］  Chen R B， Qin D T， Yi Y Y， et al. Dynamic characteristics of electromechanical coupling of wind turbine drive system under multi-source excitation[J]. Wind Energy， 2022， 25（3）： 391-418.

（編辑  吕建斌）