如何借助尺规画图帮助学生理解平行四边形的特征

黄建

教学中，教师可以借助尺规画图的方式，帮助学生更好地理解平行四边形的特征。具体可以采用以下教学过程。

一、根据要求选择线段，并在想象后进行实际操作

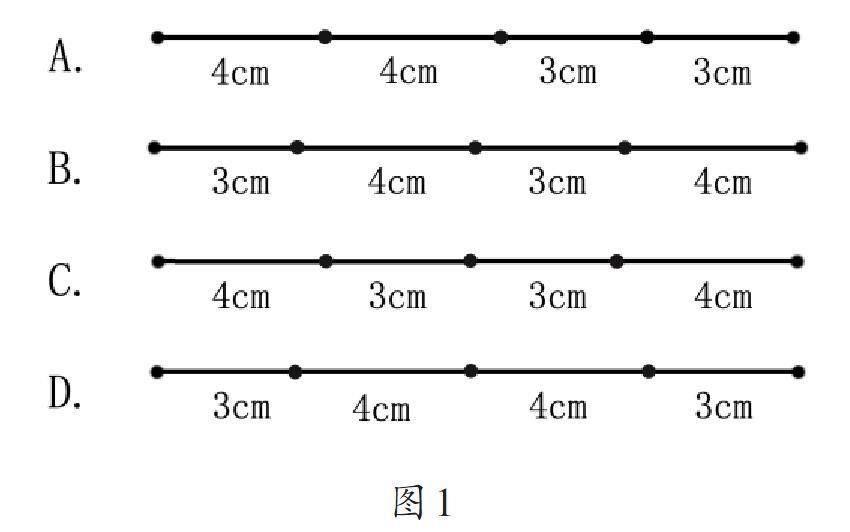
教师呈现图1，引导学生根据给出的记号，判断哪一条线段折叠后能够形成一个平行四边形。

学生先独立思考，再小组交流。

接着，引导学生思考：为什么选B？在学生解释原因的过程中，帮助他们理解平行四边形中边的特征，即平行四边形的对边长度相等。

教师提问：“请你们想象一下，这个平行四边形具体可能会是什么形状？”为了让学生更直观地理解可能的形状，教师建议学生利用学具进行实际操作，先拼接线段，然后尝试不同的拉伸方式。在操作活动中，学生发现：平行四边形的边长已经确定，但形状并非唯一。

二、布置作图任务，使用尺规工具绘制平行四边形

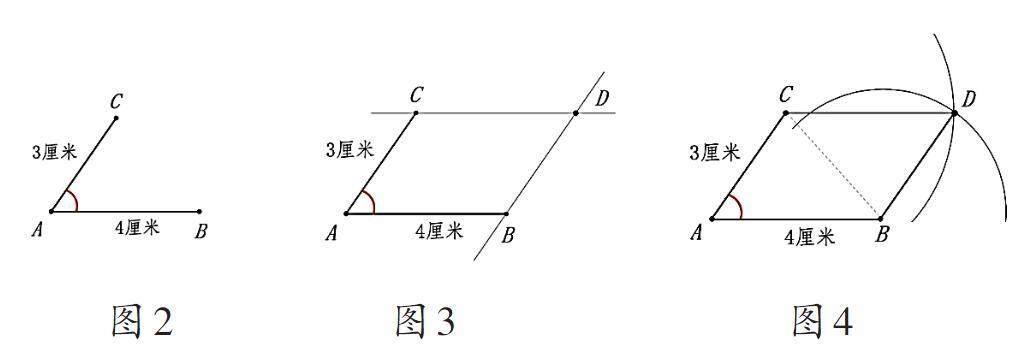
教师呈现图2，展示平行四边形的两条相邻边，提问：“若角CAB的度数确定，通过图中所示条件，能否确定这个平行四边形的形状是唯一的？”让学生根据已知条件，利用两把直尺和圆规，尝试补全这个平行四边形，并探究其形状的唯一性。

学生独立操作，用多种方法画平行四边形。

方法1：依据平行线的性质。通过点B，仅能绘制一条与AC平行的直线；同理，通过点C，也只能绘制一条与AB平行的直线。这两条平行线的交点即为顶点D，如图3所示。

方法2：运用圆规作图。首先以点C为圆心，绘制一个半径为4厘米的圆；然后以点B为圆心，繪制一个半径为3厘米的圆。两圆的交点即为所求顶点D，如图4所示。

引导学生思考：为何两圆的交点即为顶点D？帮助他们理解：顶点D至点B的距离固定为3厘米，顶点D至点C的距离固定为4厘米。当两组对边长度分别相等时，即可构成一个平行四边形。两圆的交点满足这一条件，故为所求顶点D。

对比这两种方法，它们的共同点即都在寻找交点。第一种方法寻找的是平行线的交点，其依据是平行四边形的对边分别平行；第二种方法寻找的是圆轨迹的交点，其依据是平行四边形的对边长度相等。因此，当平行四边形两条邻边的长度及其夹角确定后，其形状便已固定下来。

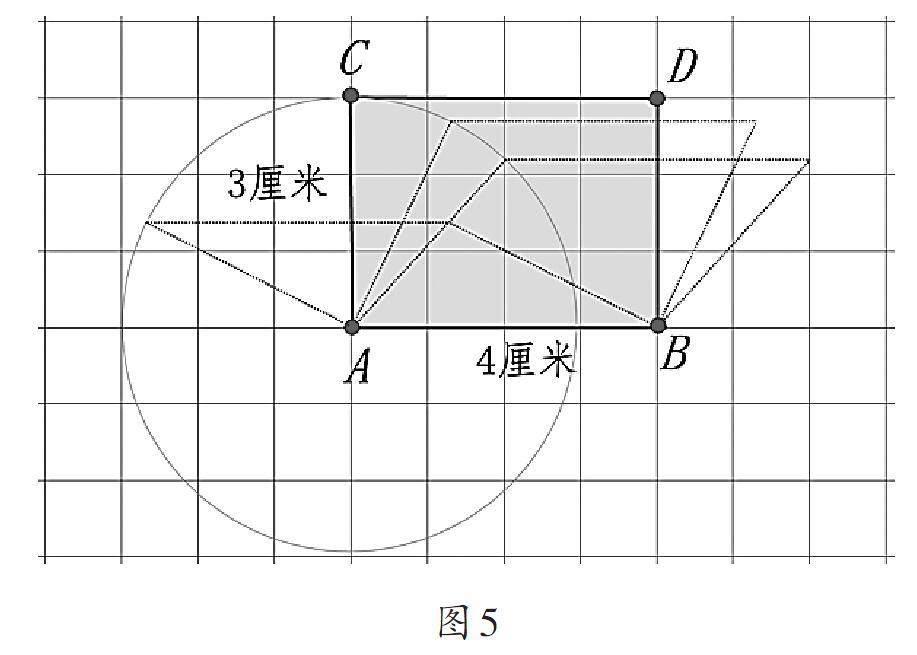
在图4的基础上，教师利用课件动态演示平行四边形两条邻边确定但其夹角不确定的情况。在观察过程中，学生发现：平行四边形的周长始终保持不变，但其面积却会发生变化（如图5）。当AC垂直于AB时（即成长方形），平行四边形的高达到最大值，从而面积也达到最大值。

上述教学过程，让学生在实物操作活动中，体会平行四边形的不稳定性。同时，通过尺规作图与想象，加深学生对平行四边形特征的理解。

（浙江省杭州市胜利实验学校）