一种融合乌鸦搜索算法的K-means 聚类算法

高海宾

（淮南联合大学 信息工程学院，安徽 淮南，232001）

聚类分析作为一种无监督学习方法，在科研领域中扮演着至关重要的角色。它广泛应用于数据挖掘、模式识别、图像分析等领域，为科研人员提供了强大的工具来解决各种问题。其中，K-means 聚类算法因其简单易用、计算效率高的特点而备受青睐。

然而，传统的K-means 算法存在一些局限性。首先，K-means 算法对初始聚类中心的选择具有数据敏感性，不同的初始值可能会导致不同的聚类结果［1］。这意味着算法的结果可能受到初始值的影响，从而影响最终的聚类效果。其次，K-means 算法基于贪心策略，容易陷入局部最优解，而无法得到全局最优解。这可能导致算法在某些情况下无法找到最佳的聚类结果。最后，K-means 算法需要预先设定聚类的数量K，但在实际操作中，K 的值往往是未知的。对于不同大小和密度的簇，K-means 算法的效果可能不佳。

为了解决这些问题，近年来不少研究者对传统的K-means 算法进行了改进和优化，以提高其在实际应用中的性能。研究者们提出了多种改进策略，其中包括通过初始化方法的改进、结合其他算法进行改进以及算法本身的改进。

（1）通过初始化方法的改进可以改善聚类效果。汪涛［2］在其研究中提出基于实测数据的WiFi 室内定位技术，通过优化初始聚类中心的选择，改善了定位的准确性。尹忠东等［3］提出了基于K-means 聚 类的配网变压器绕组材质辨识算法，通过改进初始化方法提高了聚类效果。（2）通过结合其他算法进行改进可以增强算法处理复杂数据的能力。例如，陈晓曼和苏欢［4］结合核K-means 和自组织映射（SOM）神经网络算法进行海况聚类分析，增强了算法处理复杂数据的能力。朱坤等［5］将EEMD、K-means 和蚁狮优化-长短期记忆神经网络（ALO-LSTM）相结合进行短期光伏功率预测，提高了预测精度。（3）算法本身的改进也可以提升性能。彭海驹等［6］人通过融合K-means 聚类与豪斯多夫距离（Hausdorff）来改进点云精简算法，提升了算法在点云处理上的性能。孙宇航等［7］利用核主成分分析-K 均值聚类算法（KPCA-K-means++）进行数据挖掘，优化了二次风燃烧过程。

乌鸦搜索算法（Crow Search Algorithm,CSA）作为一种新兴的群体智能优化算法，模拟了乌鸦的智能行为。与传统K-means 算法相比，乌鸦算法在全局搜索能力上具有明显优势，能够更有效地跳出局部最优解，寻找到全局最优解。此外，乌鸦算法的参数较少，易于实现和调整，适合解决高维和复杂的优化问题。基于CSA 和K-means 的优势和不足，提出了一种融合两种算法的聚类算法（CSKM），以解决传统K-means 算法在聚类分析中存在的问题。

1 相关算法介绍

1.1 K-means 算法

K-means 算法是一种基于距离的聚类算法，也称为K 均值聚类算法。该算法采用距离作为相似性的评价指标，认为两个对象的距离越近，其相似度就越大［8］。K-means 聚类算法的核心思想是以空间中K 个点为中心进行聚类，对最靠近它们的对象进行归类。

在算法执行过程中，首先从样本集中随机选取K 个样本作为簇中心，然后计算所有样本与这K 个簇中心的距离，对于每一个样本，将其划分到与其距离最近的簇中心所在的簇中。对于新的簇，重新计算各个簇的新的簇中心。这个过程会重复进行，直到满足收敛要求，即确定的中心点不再改变。下面是关于K-means 算法的详细介绍。

Step1 初始化：选择K 个初始中心点，可以采用随机选择或者基于某种启发式策略。定义数据集，D={x(1),x(2),...,x(m)},是一个n 维的实数向量。

Step2 分配阶段：对于每个数据点，计算其与各个中心点之间的距离。这里的距离度量通常采用欧式距离（Euclidean distance）。定义目标函数为

其中，m 为数据集D 的规模，k 表示聚类的数目，c(j)为第i 个簇标签，u 为聚类质心数组，为第j 个簇的质心为第i 个数据样本和第j 个簇的欧式距离。

Step3 更新阶段：对于每个簇，重新计算其中心点，即该簇内所有数据点的均值。新的中心点将作为下一轮迭代的初始中心点。最小化目标函数为

Step4 迭代终止条件：（1）重复step2 和step3，直到满足以下任一条件：中心点不再发生变化，即达到收敛状态；（2）达到预先定义的最大迭代次数。

K-means 算法的特点是简单直观、容易实现、对处理大数据集有一定的效率，并且在某些情况下能够找到最优解。然而，该算法也有一些局限性，例如对初始簇中心的随机选择比较敏感，可能会导致不同的聚类结果。此外，K-means 算法还要求用户提前设定簇的数量K，这是一个需要经验和实际需求来决定的参数。

1.2 乌鸦搜索算法

乌鸦搜索算法（CSA）是一种新兴的群体智能优化算法［9］，其灵感来源于乌鸦的隐藏食物和盗窃行为,以乌鸦的智能行为为基础，通过模拟乌鸦的食物寻找和存储策略来寻找全局最优解。乌鸦不仅能隐藏食物以备不时之需，还能观察并学习其他乌鸦的隐藏地点，以盗取食物。乌鸦非常贪婪，它们会相互跟踪，并偷取对方的存粮。不过跟踪行动并不是一件容易的工作，因为如果乌鸦发现另一只乌鸦在跟踪它，它就会试图跑到别的地方来迷惑跟踪者。CSA 正是基于这种行为，将乌鸦的食物寻找和隐藏行为抽象为优化过程中的解，搜索和更新策略。算法主要包括以下几个步骤。

Step1 初始化：随机生成一群乌鸦的位置，作为初始解集。乌鸦位置定义为向量xi,iter(i=1,2...N;iter=1,2...itermax)，N 表示乌鸦的数量，itermax表示最大的迭代次数。

Step2 记忆更新：每只乌鸦都有一个记忆，用于存储其历史上发现的最佳食物隐藏地点（即最优解）的位置，xi,iter=其中d 表示决策变量的维度。

Step3 跟随或探索：乌鸦i 通过观察并跟踪乌鸦j的行为，飞向乌鸦j 的隐藏食物地点mj,iter，这一过程模拟了乌鸦的盗窃行为，如式（3）所示。

其中，ri为0 到1 之间的随机数，感知概率参数AP用来判断乌鸦j 是否发现乌鸦i 的跟踪行为，fli,iter为乌鸦在当前迭代次数iter下的飞行距离。

如果跟踪失败，乌鸦i 跟踪行为被乌鸦j 发现，乌鸦j 引导乌鸦i 到一个随机的新位置。对以上两种乌鸦行为进行总结可得，

Step4 适应性更新：根据乌鸦的位置评估其适应度（即解的质量），并根据评估结果更新记忆中的最佳食物源位置。

Step5 迭代：重复步骤Step2 至Step4，直至满足停止条件（达到最大迭代次数或解的质量满足预设标准）。

CSA 的主要优势在于其简单的概念和易于实现的特性，以及良好的全局搜索能力和较快的收敛速率。CSA 已被成功应用于多个领域，包括机器学习、工程优化、资源分配和路径规划等。通过适当的定制和参数调整，CSA 能够有效解决这些领域中的优化问题。

2 融合乌鸦搜索算法的K-Means 聚类算法实验设计

2.1 Seeds 数据集

实验选用Seeds 小麦种子数据集进行聚类分析，重点对数据集的聚类效果进行评价。Seeds 小麦数据集是关于不同品种小麦籽粒几何特征的数据集，它一共涵盖了来自3 个不同品种的麦粒（Kama,Rosa和Canadian）的测量资料，每种麦粒包括70 个样本，总计有210 项数据记录。每项数据记录描绘了一粒小麦种 子的属 性，涉及面 积（Area）、边界长 度（Perimeter）、紧密度（Compactness）、种子长 度（Length）、种子宽度（Width）、不对称指数（Asymmetry.Coeff）、种子腹槽长度（Kernel.Groove）等7 个属性，如表1 所示。

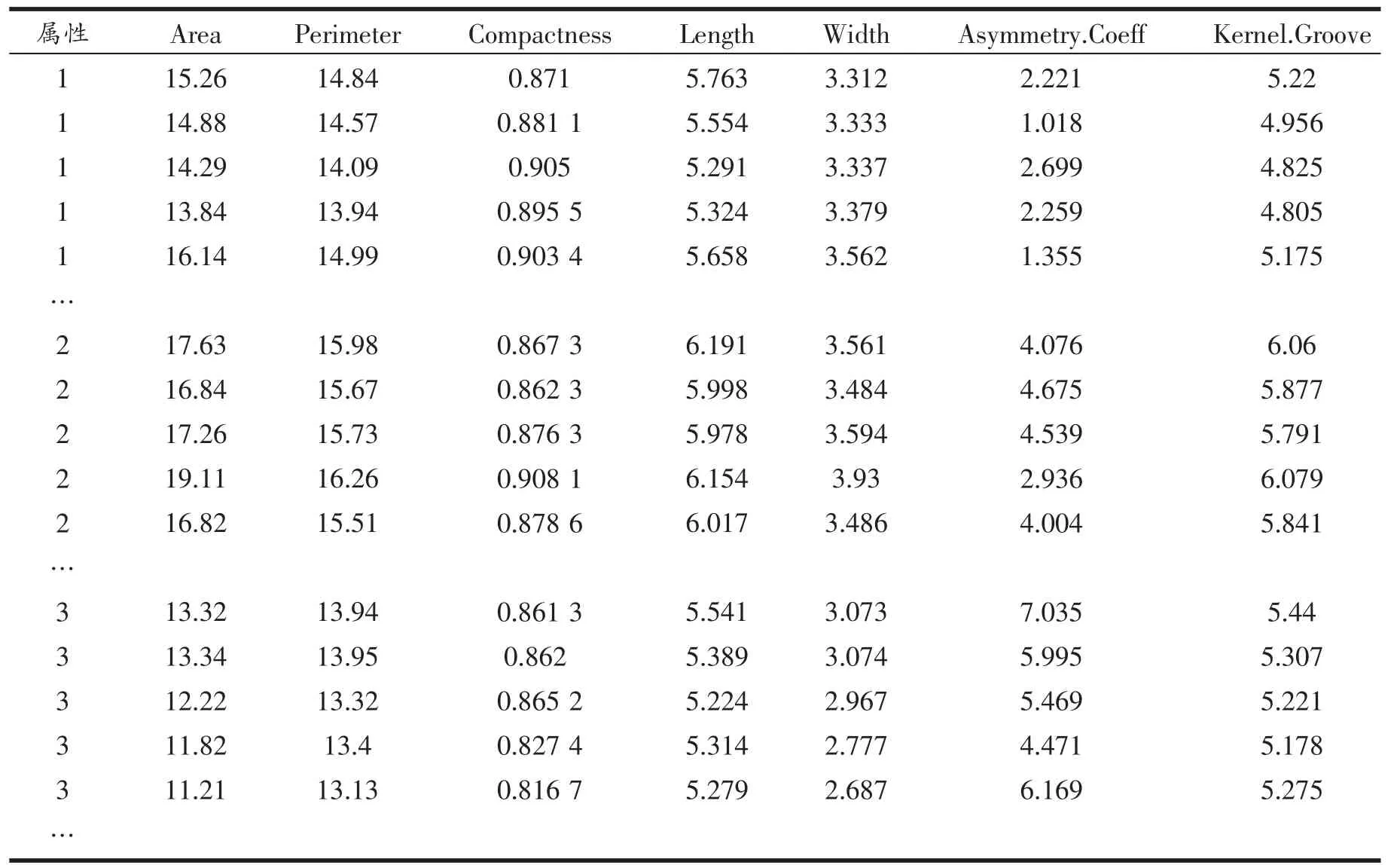
表1 小麦种子（Seeds）数据集

2.2 Calinski-Harabasz 指数

Calinski-Harabasz（CH 指数）是一种用于评估聚类效果的指标，它通过计算簇间离散度与簇内离散度的比值来评估聚类效果。CH 指数的本质是：簇间距离与簇内距离的比值，且整体计算过程与方差计算方式类似，所以又被称为方差比准则。

在规模为m 的数据集中，在聚类算法下被划分为K 个子簇，第K 个子簇的样本规模为Nk，那么第K 个子簇的CH 指数的定义为

式中tr(Bk)、tr(Wk)分别表示矩阵Bk和Wk的迹，Bk为子簇之间的离差矩阵，其定义为

式中，xi为第K 个子簇中的第i 个样本；为第K 个子簇的样本均值向量。整个样本的CH 指数定义为每个子簇的CH 指数的平均值，即

总的来说，CH 指数越高，表示聚类效果越好，即簇内样本点越紧密，同时簇之间的距离越大。CH 指数适用于多种聚类算法，并且可以用于确定最佳的聚类数目。在实际应用中，通常会尝试不同的簇数目，然后选择使CH 指数最大的聚类结果作为最终方案。不仅考虑了簇内样本的相似度，还考虑了簇间样本的差异度，从而能够更准确地反映数据的内在结构。

2.3 融合乌鸦搜索算法的K-means 算法模型

借鉴乌鸦在觅食与储存食物过程中的智能行为，本文提出了一种融合乌鸦搜索算法与K-means算法的新型聚类方法，命名为Crow Search K-means（CSKM）算法。该算法利用乌鸦搜索算法出色的全局搜索和局部开发能力，通过模仿乌鸦的智能行为，优化K-means 聚类分析中的簇数K 值处理，实现对Kmeans 算法中最佳K 值的精确寻优。

在CSKM 算法的实现中，首先初始化一群乌鸦的位置，即不同的K 值。每只乌鸦代表一个候选解，即一个可能的聚类数目。在迭代过程中，每只乌鸦尝试通过在其当前位置周围进行随机搜索来改善自己的位置，即调整K 值。这一过程通过对每只乌鸦当前K 值进行随机偏移并保持其在给定的范围内来实现。对于每个新生成的K 值，使用K-means 聚类算法对数据集X 进行聚类，并采用CH 指数作为评价标准来评估聚类质量。若新的CH 指数值高于乌鸦当前的值，则更新该乌鸦的位置和CH 指数。

此外，算法记录下所有乌鸦中最好的CH 指数及相应的K 值。为了增加算法的探索能力，对于那些在迭代过程中没有找到更优位置的乌鸦，通过随机重新分配K 值的方式来增强其探索新空间的机会。经过设定的最大迭代次数后，算法输出最佳的聚类数目及其对应的CH 指数，算法的伪代码如表2 所示。

首先，算法初始化了一些变量，包括乌鸦数量n_crows、随机生成的k_values 数组（表示每只乌鸦的位置），以及scores 数组（表示每只乌鸦当前位置的CH 指数）。最佳CH 指数best_score 被初始化为负无穷大，而最佳K 值best_k 被初始化为None。

然后，算法进入一个迭代过程，最多执行max_iter 次。在每次迭代中，算法遍历每只乌鸦，并尝试更新它们的位置和评分。具体来说，对于每只乌鸦j，算法首先计算一个新的K 值k_new，该值是当前位置加上一个随机生成的在［-1,1］范围内的整数。然后，将k_new 限制在［k_min,k_max］范围内，并对数据集X 进行K-means 聚类，得到每个样本所属的簇标签labels。接着，根据当前的簇划分计算CH 指数score_new。如果score_new 大于当前位置的scores［j］，则更新乌鸦j 的位置为k_new，并将CH 指数更新为score_new。同时，如果scores［j］大于当前最佳CH 指数best_score，则更新最佳CH 指数为scores［j］，并将最佳K 值更新为k_values［j］。

在每次迭代结束后，没有找到最佳位置的乌鸦会被随机分配新位置，并将它们的位置更新到k_values 中。最后，当达到最大迭代次数时，算法返回最佳K 值和最佳CH 指数。

3 实验结果及分析

在PyCharm 集成开发环境中对Seeds 数据集进行聚类实验，评估CSKM 聚类算法的有效性和可靠性。算法的初始参数设置最大迭代次数为5 000，种群总数为50，K 的值设置上限为10，下限为2。为了直观显示K 值和CH 指数之间的关系，使用Matplotlib 库中的plot（）函数绘制了折线图，如图1所示。

图1 CSKM 算法中最佳K 值的选择

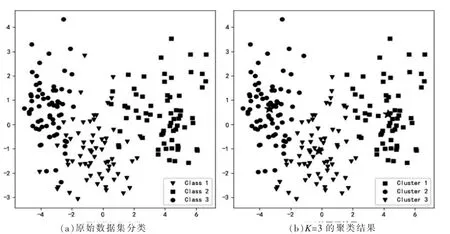
图2 原始分类和CSKM 算法聚类的散点图

从图中可以看出，当K=3 时，CH 指数达到最高点，表明聚类效果在K=3 时达到最优。根据实验结果，当K=2 时，CH 指数为344.28，随着K 值的增大，该指数先是上升至362.74（K=3），表明聚类效果在K=3 时达到一个较高水平。然而，随着K 值继续增大，CH 指数开始逐渐减小，直到K=10 时降到269.06。这一变化趋势表明，在K=3 时，聚类具有较高的类间差异性和较低的类内差异性，是本次实验条件下的最优聚类数目。实验完成后，函数返回最优K 值为3，CH 指数为362.74。

为了验证CSKM 算法的有效性和可靠性，并避免仅依赖CH 指数选择K 值可能带来的局限性，对Seeds 数据集又进行了多次聚类实验。详细评估算法在不同K 值下的性能表现，并计算了多个评价指标，包括轮廓系数、CH 指数、Davies-Bouldin 指数、调整兰德指数（ARI）、调整互信息指数（AMI）、V-measure以及Fowlkes-Mallows 指数（FMI）。这些指标从多个维度综合反映了聚类结果的质量，具体实验结果如表3 所示。

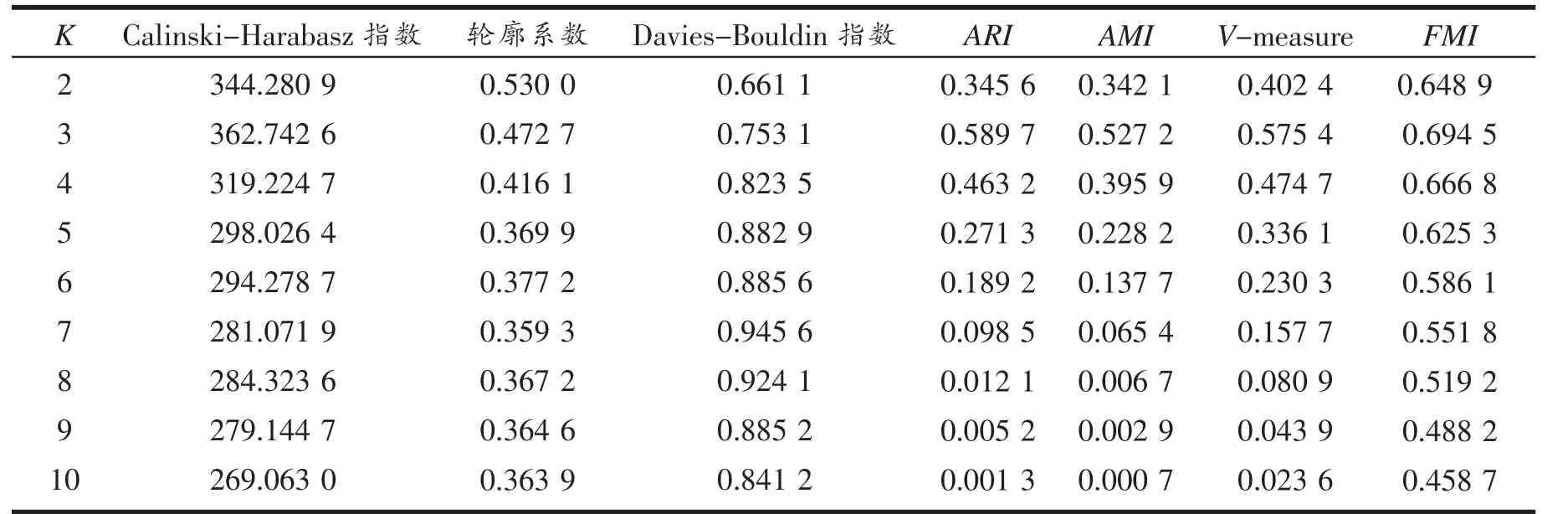
表3 聚类实验评价结果

由表3 可见，当K=2 时，算法展现出相对较高的轮廓系数（0.530），表明簇内的样本比较紧凑且簇间较为分离。同时，CH 指数为344.28，Davies-Bouldin指数为0.661，这些指标表明了算法有较好的聚类性能。此 外，ARI、AMI 和V-measure 分别为0.345 6、0.342 1 和0.402 4，FMI 为0.648 9，这些指标进一步证实了聚类结果的有效性。

随着K 值的增加，轮廓系数逐渐降低，而CH 指数在K=3 时达到最高值362.74，之后也呈现下降趋势。Davies-Bouldin 指数整体上升，表明簇间相似度增加，聚类效果有所下降。特别是在K=3 时，ARI、AMI 和V-measure 显示出较高的值（分别为0.589 7、0.527 2 和0.575 4），FMI 为0.694 5，这表明在K=3时聚类结果相对较优。

然而，随着K 值继续增加至10，所有评价指标均显示出性能下降的趋势。尤其是ARI、AMI 和Vmeasure 在K 增加时显著降低，这表明聚类的一致性和准确性随着聚类数目的增加而降低。例如，当K=10 时，ARI 仅 为0.001 3，AMI 为0.000 7，V-measure为0.023 6，FMI 为0.458 7，这些指标均表明在较高的K 值下聚类效果显著下降。

通过分析不同K 值下的聚类评价指标，可以发现K=3 时聚类结果最为理想。这一发现为Seeds 数据集的最优聚类数目提供了重要参考，并证明了CSKM 算法能够处理此类数据集时的有效性和适用性。

为了更直观地观察聚类结果，首先采用主成分分析（PCA）对Seeds 数据集进行降维处理。随后，通过CSKM 算法对降维后的数据执行聚类分析。为了可视化聚类效果，绘制散点图对原始数据集的分类和聚类结果进行对比。在2（a）图中，展示了原始分类的散点图，而2（b）图则展示K=3 时聚类效果的散点图。在散点图中，每个簇的中心以五角星标记。从图中可以观察到，当K=3 时，除了簇1 和簇2 之间存在一些重叠部分的错误分类，以及簇3 中的部分样本分类错误之外，绝大多数样本的聚类效果与原始数据集的分类结果相一致，而且簇中心的位置基本保持一致。总体而言，聚类效果达到了较为理想的水平。

4 结束语

通过实验和分析，可以看出CSKM 算法在聚类Seeds 数据集时表现出了良好的性能。相对于传统的K-means 算法，CSKM 算法具有以下优势：

（1）自动确定最佳K 值。传统K-means 算法中，用户需要事先设定K 值，这往往需要多次尝试。而CSKM 算法通过乌鸦搜索算法自动寻找最佳K 值，降低了人为干预的局限性，提高了算法的适用性和泛化能力。

（2）增强全局优化能力。CSKM 算法采用自然启发式算法（乌鸦搜索算法）进行优化，具有较强的全局优化能力。这有助于避免陷入局部最优解，提高聚类效果。

（3）提高计算效率。由于CSKM 算法能够自动寻找最佳K 值，因此在实际应用中可能需要较少的迭代次数和计算资源，从而提高计算效率。

（4）结果稳定性好。CSKM 算法通过优化过程确定最佳K 值，使得聚类结果具有较好的稳定性，不易受到初始值和参数设置的影响。

此外，研究的评价结果可能受到数据集本身特性的影响，因此在实际应用中需要结合具体问题和数据特点进行综合考虑。未来的研究可以进一步探讨如何优化CSKM 算法的参数设置，以优化聚类效果。同时，也可以尝试将该算法应用于其他领域的数据分析中，以验证其泛化能力。