基于多保真度神经网络的超材料力学性能预测

□ 邱荣英 □ 李钼石 □ 刘 钊

1.泛亚汽车技术中心有限公司 上海 200120

2.上海交通大学 机械与动力工程学院 上海 200240

3.上海交通大学 设计学院 上海 200240

1 研究背景

超材料具有介观结构的几何特征及传统材料无法获取的特殊力学性能,超材料的特性可以通过改变介观结构单胞的设计来调整,超材料的增材制造为开发下一代轻质功能性汽车部件开辟了新的机会。超材料填充结构具有两种尺度的几何特征,如图1所示。在介观尺度下,每个超材料单胞被设计用于实现特殊的局部特性。在宏观尺度上,通过组装超材料细胞来创建结构产品。

图1 超材料填充结构

为了达到超材料的最优表现,如比刚度最大、吸能最大的最佳力学性能,散热最快的最佳热力学性能,最佳声学性质等,需要在两个尺度上定义设计变量,以优化系统性能。在现有技术中,均质化法和固体各向同性材料惩罚模型等拓扑优化已被用于生成宏观尺度结构,其中包含各种密度水平的灰色单元,灰色单元被转换为预定义模式的介观结构。然而,相同密度水平的不同介观结构设计可能具有非常不同的性能。为了解决这个问题,学者们已经开发出了一种参数化水平集方法来同时优化结构和填充超材料单胞。上述方法依赖于基于梯度的优化算法,考虑到冲击、碰撞、爆炸等瞬态非线性行为,解析梯度无法用于结构优化,因为数值和物理噪声及分岔会加剧瞬态动态模拟的高非线性程度。考虑到传统的预测方法存在明显的局限性,学者们提出使用数据驱动的方法来提升超材料力学性能的预测效率与准确性。

显然,数据驱动设计效果的优劣取决于数据保真度与数据量,其中保真度指数据或模型与客观规律的相似程度。已有研究中,超材料力学性能数据有物理试验与仿真分析两种获取方式。物理试验数据采集过程复杂,人力、时间成本耗费大,难以达到满足建模精度的数据量。随着超算应用的普及,仿真数据的获取成本大幅降低,短时间即可生成十万甚至百万量级的数据,但仿真数据和试验相比往往存在一定的误差,基于仿真数据的优化设计效果会具有一定的局限性。由此,仅使用单一来源的数据难以满足超材料力学性能优化设计对数据保真度与数据量的需求。工业设计领域中,学者们常常使用多保真度代理模型融合不同来源的数据集构建模型来解决类似问题。遗憾的是,由于超材料具有力学性能数据输入变量多、非线性强、不同来源数据成本差异极大的特点,已有的多保真度代理模型构建方法拟合效果较差。

为解决上述问题,笔者提出一种基于神经网络与迁移学习思想的多保真度代理模型构建方法,基于此方法构建多保真度神经网络的超材料力学性能预测框架。框架针对超材料力学性能预测问题与多保真度代理模型的特性,对传统数据驱动框架进行改进与完善,提升设计精度与效率。笔者以具体工程问题为例,阐明方法的效果与优势。

2 技术基础

2.1 神经网络

神经网络是许多个神经元按一定的层次结构连接组成的机器学习模型,最基本成分神经元模型具体形式如图2所示。其中,xi表示第i个输入变量,wi表示第i个输入变量的权重,b表示神经元的偏置,f()表示神经元的激活函数,y表示神经元的输出。

图2 神经元模型具体形式

作为工程问题中常用的代理模型,具有多层神经元的神经网络具有较强的数据拟合能力。给定训练数据集后,各个神经元的权重与偏置可以通过训练获得。误差逆传播算法是目前最常用的训练方法,具体流程为:首先将输入提供给输入层神经元,逐层将信号前传,直到产生输出层结果;然后计算输出层的误差,将误差逆传播至各层神经元;最后根据各层神经元的误差来对各个神经元的权重与偏置进行调整。迭代过程循环进行,直至达到停止条件,即可获得预测精度较高的神经网络。

2.2 迁移学习

迁移学习作为机器学习的一个重要分支,是解决小样本问题的重要手段,广泛应用于图像识别、自然语言处理等领域。迁移学习的基本思想为:当两个模型描述的问题不同但相关,且两个模型的形式与结构一致时,他们的模型参数也存在相似性;如果构建其中一个模型所需的数据不足,模型参数可以通过对另一个模型的参数进行微调获得。

在本研究中,神经网络与迁移学习思想被应用于多保真度代理模型的构建。拟合低保真度数据的神经网络与拟合高保真度数据的神经网络间必然存在相似性,通过控制训练过程的方式,可以人为将相似性集中于神经网络的前几层,称为通用特征层,并在后几层,称为特定特征层,体现出差异性。由此,大量的低保真度数据可以被应用于保证两个神经网络前几层的有效性,只需要少量高保真度数据,即可完成对拟合高保真度数据的神经网络的训练。

3 预测框架

针对现有技术存在的不足,本研究提出一种基于迁移学习-多保真度建模的介观结构件力学性能预测方法,使用低保真度数据训练低保真度神经网络,基于迁移学习中的微调方法,使用高保真度数据重训练低保真度神经网络,获得最终的多保真度神经网络模型,多保真度神经网络可以以较高的精度预测介观结构件对应的力学性能。预测流程如图3所示。这一方法可融合不同保真度数据进行建模,并且相比传统的协同克里金算法对高保真度数据需求量较少,降低了介观力学性能的预测成本。预测框架包括如下步骤:

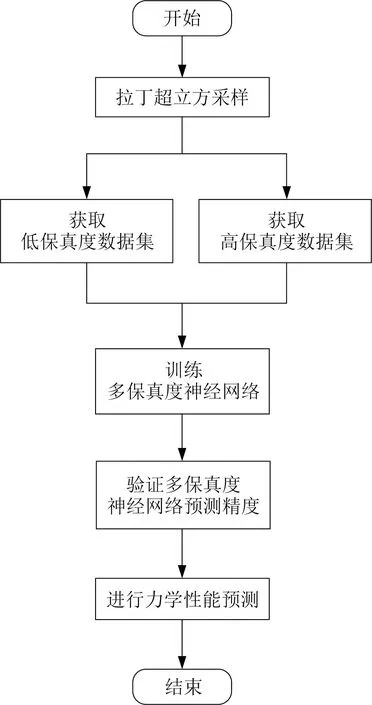
图3 预测流程

(1) 初始化多保真度神经网络,即定义多保真度神经网络的输入与输出,并定义多保真度神经网络的网络结构;

(2) 重复进行拉丁超立方采样,对训练数据集与测试数据集中样本点的输入进行设计,训练数据集包含低保真度数据集与高保真度数据集两个子集,用于训练多保真度神经网络,测试数据集用于计算多保真度神经网络的精度;

(3) 基于有限元仿真获取训练数据集与验证数据集中样本点的输出;

(4) 基于多保真度训练数据集,结合迁移学习思想,构建多保真度神经网络;

(5) 基于多保真度神经网络,测试样本集中样本点的输出,并计算R2参数,表征预测精度,判断是否达到精度要求;

(6) 根据获得的多保真度神经网络模型进行力学性能预测。

R2参数是一种用于评估回归模型拟合优度的统计量,表示因变量的方差中可由自变量解释部分所占的比例。

多保真度神经网络架构如图4所示,包含输入层、通用特征层、两组具有相同架构的特定特征层、输出层。一组数据经输入层进入网络,首先经由通用特征层得到一组维度与通用特征层最后一层中神经元数量一致的输出,即通用特征输出。接着将通用特征输出作为输入,分别输入两组特定特征层,经由这两组特定特征层的变换后得到对应保真度的输出。面向不同的数据集时,多保真度神经网络具体架构的超参数会存在差异,如通用特征层数量、特定特征层数量、各隐藏层中的神经元数量等。

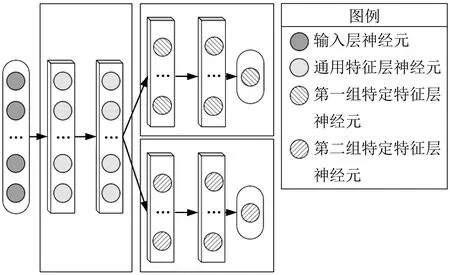
图4 多保真度神经网络架构

为了训练多保真度神经网络,提出一个新的损失函数:

Loss=Loss1+αLoss2

(1)

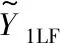
损失函数的核心思想为使训练过程中特定特征层的参数只受对应数据集预测精度的影响,通用特征层参数受两个数据集预测精度的共同影响,以此控制神经网络学习到的通用特征最大化。

多保真度神经网络比传统多保真度代理模型精度更高,更适用于超材料力学性能预测,这主要有两点原因。一是神经网络的基本原理为空间变换,由于神经网络的层次结构,这种空间变换是逐层实现的,数据每经过一层神经元都是一次空间变换,拟合低保真度数据的神经网络与拟合高保真度数据的神经网络间必然存在相似性,通过控制训练过程的方式,可以人为将相似性集中于神经网络的前几层,以最大化利用不同保真度数据集,从而显著提升多保真度代理模型的精度。二是神经网络训练方法为分批次训练的方式,这样的方式不会受到数据量的影响,而使用过大的数据训练以传统的协同克里金算法等模型为基底的多保真度代理模型时,容易出现内存溢出、拟合失败的情况。

4 预测实例

4.1 问题定义

为研究涉及的介观单胞结构,三种不同的单胞具有不同的杨氏模量与泊松比,如图5所示。介观结构网格如图6所示,加载工况如图7所示。笔者以此为例,验证所提出框架的有效性。在矩形设计网格中填充3×4个介观结构单元,构建二维矩形板。为采集不同保真度的数据集,建立两种不同精度的有限元模型。高保真度有限元模型具有足够高的分辨率,因此可以捕获每个单元的介观结构几何特征。基础材料钢的属性被分配给高保真度有限元模型的每个网格单元,基础材料的杨氏模量为210 000 MPa,泊松比为0.3,密度为7.9 g/cm3。在低保真度有限元模型中,每个介观结构细胞由一个网格单元表示,并赋予每个网格相应介观结构单胞的均质化等效泊松比与弹性模量。加载工况下,介观结构件为一边固定边界、两边自由边界、一边受5 000 N均布力压缩。研究的目标是预测在加载工况下介观结构件顶端中点的位移。

图5 三种介观单胞结构

图6 介观结构网格

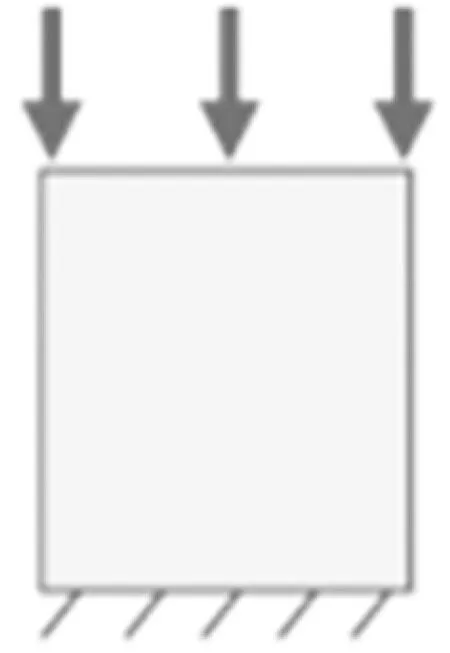
图7 加载工况

4.2 高低保真度数据采集

本研究的高低保真度数据集自动化构建采集流程如图8所示。

图8 高低保真度数据集采集流程

(1) 根据超材料结构预测的任务要求,确定设计变量、设计空间,设定初始样本点数为400,并令迭代计数参数i为1。

(2) 当i为1时,进行初始样本点设计,采用拉丁超立方试验设计方法在设计空间内获得400个初始试验样本点输入值,保存为StaticDOE.mat。

(3) 应用MATLAB 软件读取StaticDOE.mat中样本点输入值,并依此编辑文本进行参数化建模,建立介观结构静态仿真模型inp文件,命名为i_struct_case1.inp和i_struct_case2.inp,分别对应静态压缩载荷和剪切载荷下的仿真模型。inp文件中声明了结构的节点编号、节点集合、单元编号、单元集合、材料属性、边界条件、加载方式。

(4) 应用MATLAB 软件调用命令行cmd.exe,将i_struct_case1.inp和i_struct_case2.inp分别提交至ABAQUS求解器进行计算,生成相应的输出场文件i_struct_case1.odb和i_struct_case2.odb。

(5) 应用MATLAB 软件调用Python程序post_process.py,提取出输出场文件i_struct_case1.odb和i_struct_case2.odb中最后一个框架对应的结构件上端中点的位移,并保存为文本文件NodeDisp.txt。

(6) 迭代参数i加1,重复步骤(3)至步骤(5),获取不同样本点的相应响应值,并输出为文本文件。

经过上述循环计算,构建本研究使用的高保真度与低保真度数据集,为基于迁移学习的多保真度建模提供支撑。

4.3 多保真度建模与精度比较

本研究的超材料介观结构件包含12个介观单胞结构,令多保真度神经网络的输入X为[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12]。介观结构件力学性能为加载工况下介观结构件顶端中点的位移。令多保真度神经网络的输入为Y,多保真度神经网络包含输入层、隐藏层、输出层,输入层数量为1,层内包含与输入X维度相等数量的神经元。隐藏层分为通用特征层与特定特征层,通用特征层数量为2,每层包含16个神经元,特定特征层数量为1,层内包含16个神经元。输出层数量为1,层内包含1个神经元。

训练数据集包含低保真度数据集与高保真度数据集两个子集,分别包含PTL与PTH个样本点。测试数据集包含PV个样本点。其中,训练数据集用于训练多保真度神经网络,测试数据集用于计算多保真度神经网络的精度。基于有限元仿真获取训练数据集与验证数据集中样本点的输出为Y1与Y2。低保真度数据集的输出由粗糙网格有限元仿真获得,即将介观结构件划分为12个壳单元网格,为每个壳单元赋予介观单胞结构对应的杨氏模量与泊松比。高保真度数据集的输出由精细网格有限元仿真获得,即将介观结构件粗糙网格中12个壳单元网格分别替换为对应介观单胞结构真实结构的精细网格,并为每一个精细网格壳单元赋予介观结构件材料自身的杨氏模量与泊松比。粗糙网格如图9所示,精细网格如图10所示。

图9 粗糙网格

图10 精细网格

基于训练数据集中的低保真度数据集训练低保真度神经网络,训练优化器为Adam算法,损失函数为均方误差,均方误差损失函数具体表达式为:

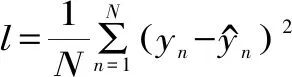
(2)

冻结低保真度神经网络的通用特征层,微调获得多保真度神经网络之后,计算R2参数,表征预测精度。R2参数表达式为:

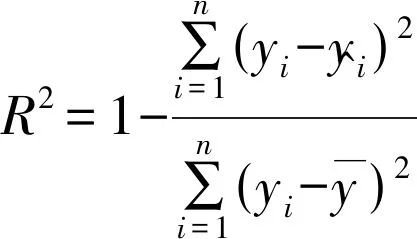
(3)

本文方法的预测精度与传统协同克里金算法的比较见表1。

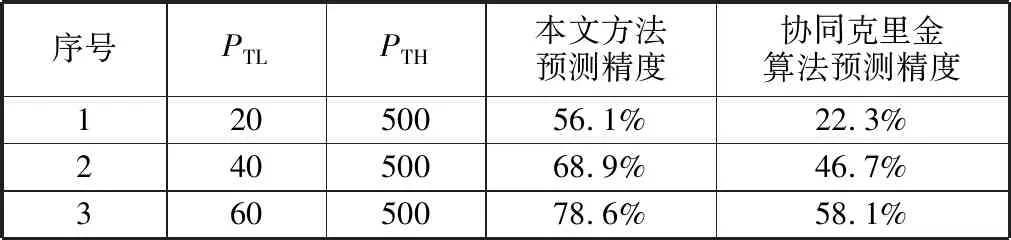
表1 预测精度比较

在三种不同的高保真度数据样本量的测试中,本文方法相比传统协同克里金算法预测精度提升20个百分点以上,即相同的成本下,本文方法的预测精度显著优于传统方法。另一方面,本文方法在PTL为20时的预测精度为56.1%,与传统方法在PTL为40时的预测精度接近,说明达到相同预测精度水平,本文方法的所需成本显著低于传统方法。

5 结束语

笔者提出一种超材料力学性能预测框架,可以用于超材料填充结构多尺度设计优化,通过集成多保真度神经网络、迁移学习算法,提高预测效率与精度。

这一方法平衡了单一来源数据在精度与开发成本上的矛盾,提高了超材料力学性能预测的效率,在实际应用中可扩展至冲击、碰撞、爆炸等瞬态非线性行为的预测。

面向超材料力学性能预测问题具有的高维、强非线性特点,提出基于神经网络与迁移学习思想的多保真度神经网络。应用案例的测试结果表明,所提出的多保真度神经网络对高成本数据的需求显著降低,且精度显著优于同样数据成本构建的其它模型。