基于数据归一化原点矩约束最大熵原理的小样本数据测量不确定度评定

□ 钟 浩 □ 张为民 □ 谢树联 □ 贾子玮

同济大学 机械与能源工程学院 上海 201804

1 研究背景

在生产制造中,测量检验是重要环节。然而,测量过程中的随机因素会造成被测量量值具有分散性。测量不确定度是表征被测量量值分散性的非负参数,可以表明测量结果的可信程度,是测量结果不可缺少的参数[1-2]。随着消费市场对产品的需求向个性化和多样化转变,越来越多的企业由大批量生产模式向多品种小批量生产模式转变。由于生产效率的要求,小批量生产时往往不可能针对特定的尺寸与形位特征进行大量测量,所获得的测量数据样本较少,此时需要在小样本测量数据下进行测量不确定度评定。

最大熵原理是Jaynes[3]提出的,核心思想是在推断一个随机变量的概率分布时,仅依靠已知信息,不对未知信息进行主观假设,由此得到信息熵最大的随机变量分布,能客观反映随机变量的分布情况。最大熵原理被应用到很多领域,并展现出巨大的实际价值和研究意义[4]。在机械制造的测量检验环节中,可以利用最大熵原理确定测量样本数据的概率密度函数,进一步完成测量不确定度的评定[5-8]。

以原点矩为约束的最大熵原理是基本且应用广泛的最大熵原理,求解概率密度函数的准确性受样本量大小和原点矩阶数影响。样本量足够大时,基于更高阶的原点矩可以得到更准确的结果。但随着阶数的增加,求解过程越来越复杂,反而使计算结果不准确[9]。因此,选择更高阶的原点矩不能解决小样本数据下基于原点矩约束最大熵原理求得的测量不确定度不可靠的问题。另一方面,当测量值较大时,基于原点矩约束最大熵原理在优化求解时有数值溢出风险[10-11]。笔者针对经典原点矩约束最大熵原理在小样本测量数据情况下求出测量不确定度不够准确可靠,存在数值溢出风险的问题,提出适用于小样本测量数据的基于数据归一化原点矩约束最大熵原理的测量不确定度评定方法,并验证有效性,为基于最大熵原理的测量不确定度评定的研究与应用提供参考。

2 数据归一化原点矩约束最大熵原理

设测量样本数据x的样本区间为[xmin,xmax],对其进行归一化处理,归一化处理后的随机变量为y,区间为[0,1],归一化公式为:

(1)

根据最大熵原理,随机变量y唯一的概率密度函数p(y)可由最大熵H(y)确定,即:

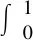
(2)

在原点矩约束条件下,有:

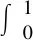
(3)

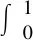
(4)

(5)

式中:mi为i阶原点矩,i=1,2,3,…,n。

使用拉格朗日乘子法在熵函数中引入拉格朗日乘子λ0、λ1、…、λn,可得:

(6)

(7)

再由式(3)、式(4)和式(7),可得:

(8)

参数λi方程组为:

(9)

设残差为ri,有:

(10)

当残差的二次方和最小时,可以求解出λi的最优解,为:

(11)

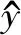
(12)

(13)

(14)

u=(xmax-xmin)σ

(15)

针对参数λi,可用非线性最小二乘法[14]、爬山搜索算法[6,13]、粒子群算法[15]、遗传算法[16]等进行优化求解。笔者采用Nelder-Mead算法求解参数λi的最优解,确定测量样本数据的概率密度函数。

3 数值仿真

在Python软件中先基于正态分布N(5,0.5)生成10个随机数,表示加工结果真实值。再基于正态分布N(0,0.1)生成100个随机数表示测量误差,每10个为1组,分别与之前10个随机数进行相加,形成10组数据。仿真随机数据见表1。

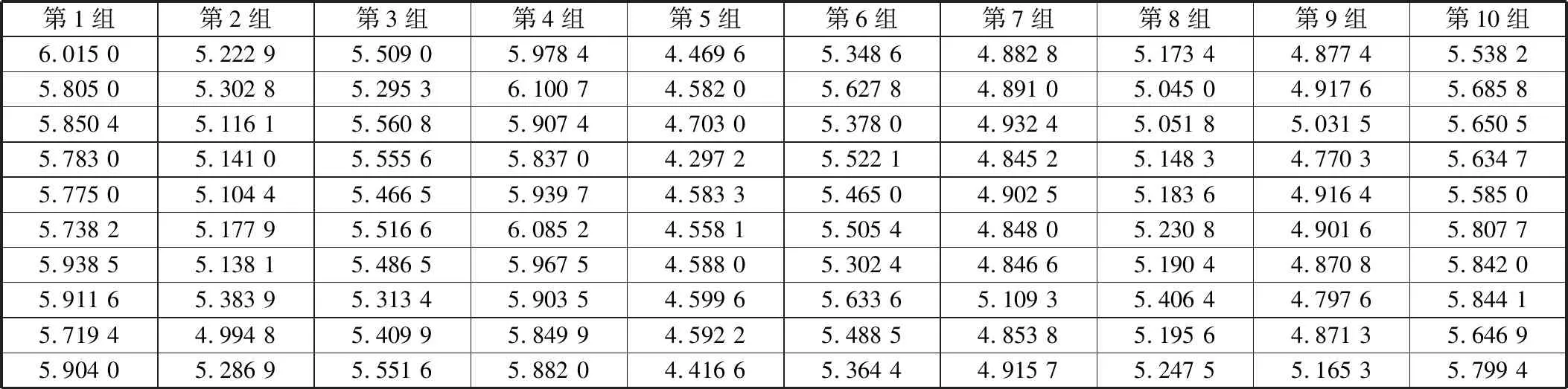
表1 仿真随机数据

使用数据归一化原点矩约束最大熵原理,对上述仿真随机数据进行测量不确定度评定。以第1组数据为例,对数据进行归一化处理,积分区间为[0,1],选择3阶矩,求得样本原点矩m1为0.421 6,m2为0.272 9,m3为0.205 4。在Python软件中编写计算程序,使用Nelder-Mead算法进行优化求解,设定λ1、λ2、λ3的初始值依次为0.5、0.5、0.1,优化得到最优解λ1为-3.680 4,λ2为3.118 3,λ3为-0.262 2,代入式(8)可得λ0为0.813 2,由此得到归一化后y的概率密度函数为:

p(y)=exp(0.813 2-3.680 4y+3.118 3y2-

0.262 2y3)

(16)

由式(12)～式(15)求得第1组数据的测量不确定度为0.091 2。以相同方式求出其它组测量不确定度。为进行比较,同时以原点矩约束最大熵原理[13]和概率权重矩约束最大熵原理[17]计算仿真随机数据的测量不确定度,且同样选择3阶矩。三种方法计算得到的测量不确定度结果见表2。三种方法计算的测量不确定度散布对比如图1所示。

图1 仿真随机数据测量不确定度散布对比

表2 仿真随机数据测量不确定度结果

从图1中可以明显看出,基于原点矩约束最大熵原理的评定结果中,有六组数据评定结果小于理论值,有三组数据评定结果大于理论值,整体评定结果分布偏于理论值下方。基于数据归一化原点矩约束最大熵原理和基于概率权重矩约束最大熵原理的评定结果较均匀地分布在理论值上下,与理论相符。三种方法计算的10组仿真随机数据的测量不确定度均值及与理论值偏差见表3。数据归一化原点矩约束最大熵原理与概率权重矩约束最大熵原理一样,更为接近理论值0.1,与理论值的相对偏差分别仅为1.9%和2.6%,而原点矩约束最大熵原理与理论值的相对偏差则达到了10.4%。三种方法中,所提的数据归一化原点矩约束最大熵原理表现最佳。由仿真随机数据的测量不确定度评定结果分析可得,数据归一化原点矩约束最大熵原理能够有效提高小样本测量数据下基于原点矩约束最大熵原理测量不确定度评定的准确性。

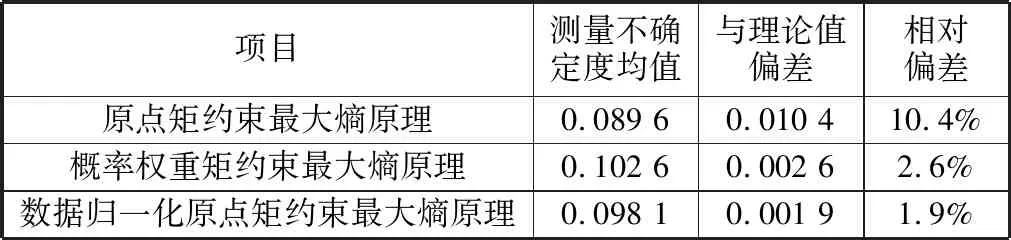
表3 仿真随机数据测量不确定度均值及与理论值偏差

4 应用案例

以某一小批量阀块零件为例,检验所提基于数据归一化原点矩约束最大熵原理的测量不确定评定方法的应用效果。使用三坐标测量机进行测量,测量阀块零件距离圆柱顶端5.5 mm处圆度,如图2所示。先对一个零件重复测量100次,将其标准差0.61 μm作为理论值。之后分别测量十个阀块零件的圆度,每个零件重复测量10次,获得的圆度测量值见表4。

图2 阀块零件圆度测量

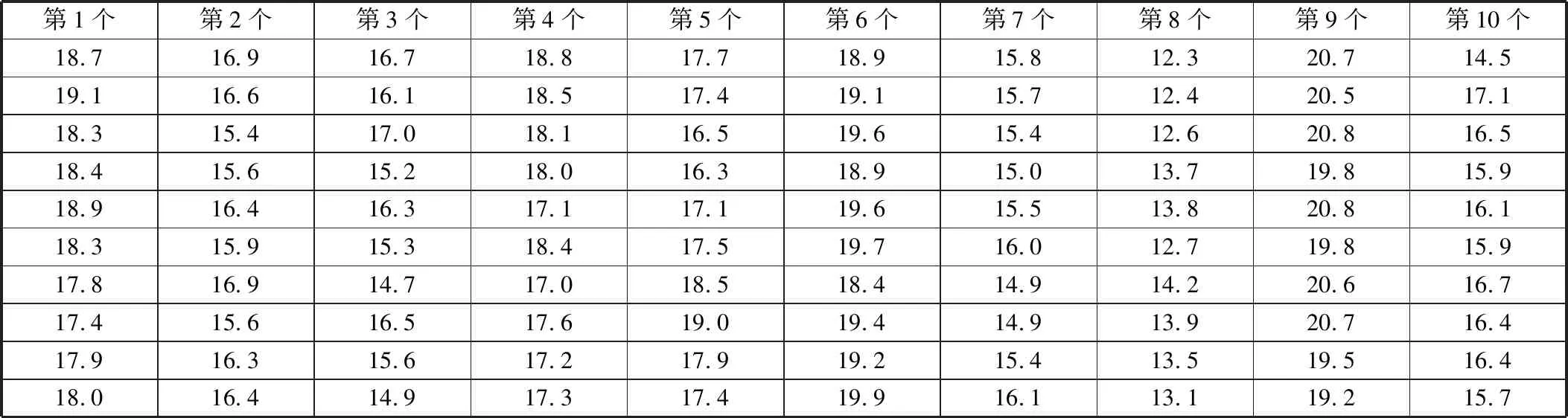
表4 阀块零件圆度重复测量数据 μm

同样采用三种方法分别计算阀块零件圆度重复性测量不确定度,计算结果见表5。三种方法计算的阀块零件圆度测量不确定度散布对比如图3所示。

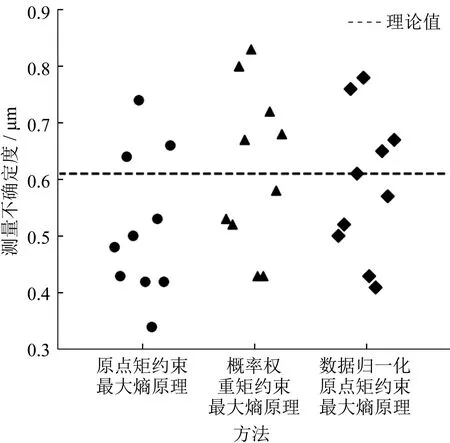
图3 阀块零件圆度测量不确定度散布对比

表5 阀块零件圆度测量不确定度

从图3中可以明显看出,基于原点矩约束最大熵原理评定的十个阀块零件的圆度测量不确定度分布偏于理论值下方,其中有七个阀块零件的评定结果小于理论值。基于数据归一化原点矩约束最大熵原理和基于概率权重矩约束最大熵原理的评定结果相对均匀地分布在理论值上下。这与仿真随机数据的测量不确定度分析结果一致。三种方法计算的十个零件的圆度测量不确定度均值及与理论值偏差见表6。 原点矩约束最大熵原理与理论值0.61 μm相对偏差为14.75%,数据归一化原点矩约束最大熵原理与理论值相对偏差为3.28%,概率权重矩约束最大熵原理与理论值相对偏差为1.64%。因此,应用案例分析再次证明了在小样本测量数据下数据归一化原点矩约束最大熵原理的有效性,能有效提升原点矩约束最大熵原理在小样本测量数据下的测量不确定度评定的准确性。

表6 阀块零件圆度测量不确定度均值及与理论值偏差

5 结束语

笔者针对小样本测量数据下基于原点矩约束最大熵原理评定的测量不确定度不准确问题,提出适用于小样本测量数据的基于数据归一化原点矩约束最大熵原理的测量不确定度评定方法,并进行数值仿真和应用案例验证。数值仿真与应用案例验证结果显示,基于数据归一化原点矩约束最大熵原理评定的测量不确定度均匀分布在理论值上下。在数值仿真验证中,10组仿真随机数据评定结果的均值与理论值的相对误差仅为1.9%,而原点矩约束最大熵原理与理论值的相对误差为10.4%。在应用案例验证圆度测量不确定度评定中,对十个阀块零件圆度的评定结果与大量重复测量的圆度测量不确定度理论值相比,相对误差为3.28%,而原点矩约束最大熵原理与理论值的相对误差为14.75%。由此,在小批量生产的测量检验环节中,对于只能获得小样本测量数据的情况,与原点矩约束最大熵原理相比,数据归一化原点矩约束最大熵原理能够准确有效评定测量不确定度,提高小样本测量数据下基于原点矩约束最大熵原理测量不确定度评定的可靠性。