闸片摩擦块排列方式对高速列车制动盘磨损深度的影响

周素霞, 王君艳*, 巴馨悦, 李光, 曲直

(1.北京建筑大学机电与车辆工程学院, 北京 100044; 2.北京建筑大学城市轨道交通车辆服役性能保障北京市重点实验室, 北京 100044)

随着现代列车逐渐向“高速化”方向发展,对于制动装置的性能要求也愈来愈高。盘式制动是列车常见制动方式之一,其主要通过制动盘和闸片上摩擦块间的相互摩擦作用,实现制动过程。磨损是制动盘主要的失效方式之一,当制动盘最深磨损位置超过单侧最大磨耗限度时需更换制动盘。由于制动盘与车轴固定在一起,拆装困难、维修成本高、重复使用率低。因此,研究制动盘磨损的影响因素,寻找减少其最大磨损深度的方法,对于延长制动盘的磨损寿命具有重要意义。

研究表明,制动初速度、制动压力和制动盘表面形态等因素对磨损有显著影响,且制动初速度越大、制动压力越高,磨损越严重[1-5]。近年来,学者们针对制动盘发生摩擦接触的摩擦块开展了大量的研究。Xiang等[6]研究了圆形、五角形、六角形3种不同形状的摩擦块对于高速列车制动界面的摩擦学行为和动力学特性的影响。结果表明,摩擦块的形状对接触应力分布和磨损特性有显著影响,合适的制动块形状可以改善列车摩擦制动系统的服役摩擦学行为。Tang等[7]研究了摩擦块穿孔结构对铁路制动系统磨损、热分布和噪声特性的影响,其结果表明摩擦块有孔结构会存储制动过程中产生的磨屑,从而减少对制动盘的磨损量。Yin等[8]研究了摩擦块的连接配置对制动系统界面摩擦学行为、热响应和振动噪声有显著影响,浮动连接方式可以抑制制动系统的振动噪声。Xiang等[9]采用高速列车上一种典型摩擦块进行了制动实验,研究了制动器界面的摩擦磨损、界面温度、振动和噪声,分析了振动响应与界面接触行为之间的相互关系,认为制动块的摩擦系数和接触角是影响制动系统振动特性的重要因素。Wu等[10]研究发现,摩擦块配置对制动系统的声压和稳定性有显著影响,特定配置的刹车片可以有效抑制刹车系统的不稳定性,降低啸叫声。Pelcastre等[11]研究了不同摩擦块材料的摩擦学性能,结果表明:烧结CBB(composite brake blocks)在冬季条件下比有机CBB具有更高的摩擦性能。文献[12-13]中通过在试验装置上进行摩擦学试验,研究摩擦块残余高度对界面摩擦学行为以及摩擦振动噪声(friction-induced vibration noise,FIVN)的影响,结果表明:随着摩擦块高度的减小,摩擦面倾角减小,摩擦界面的磨损性能较好,摩擦振动噪声越弱。然而,前人研究多集中于摩擦块材料、形状和残余高度等对制动盘温度场、应力场和噪声的影响,忽略了制动盘的磨损情况。目前对于摩擦块排布方式对制动界面摩擦磨损的研究鲜见报道,其对摩擦学行为机理的研究也尚不明确。

鉴于此,基于修正的Archard磨损模型,采用有限元法研究列车通过42号道岔紧急制动状态下3种不同摩擦块排列方式对制动盘最大磨损深度的影响。提出应力磨损因子参数来表征应力对最大磨损深度的影响,并通过制动盘节点磨损深度分析摩擦表面的磨损形貌。为减少制动盘的最大磨损深度,提高列车制动盘使用寿命提供借鉴。

1 理论模型

目前,研究磨损常用的理论模型为Archard磨损模型。文献[14-18]采用Archard磨损模型分析制动过程摩擦磨损问题。在微分时间dt内,其通用的表达方式采用微分形式为[18]

(1)

式(1)中:V为磨损体积,mm3;K为两摩擦部件之间的磨损系数;H为较软材料的表面硬度,HB;P为瞬时法向压力,N;L为相对滑移距离,mm。

瞬时磨损体积增量dV可表示为[18]

(2)

式(2)中:h为磨损深度,mm;ΔA为微小接触面积,mm2。

因此,磨损体积转化为磨损深度的计算公式为

(3)

微分时间dt内制动盘与摩擦块的接触面积ΔA如图1所示。

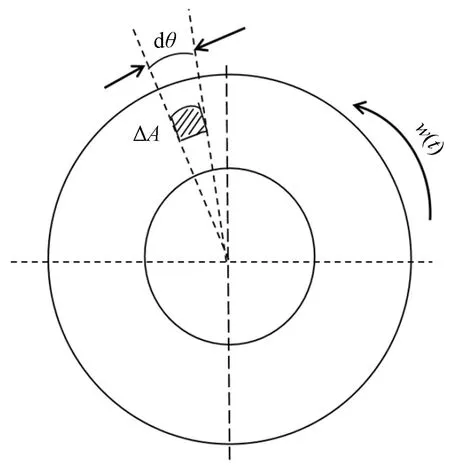
图1 微分时间dt内摩擦块与制动盘的接触面积示意图Fig.1 Schematic representation of the contact area between the friction block and the brake disc at differential time dt

由于制动盘为圆周运动,微分时间dt内制动盘与摩擦块之间的滑移线段为一段圆弧,因此dL可表示为[17]

dL=rdθ

(4)

式(4)中:r为制动盘圆心与磨损节点之间的径向距离,mm;θ为滑移距离所对应的制动盘圆心角,rad。

dθ=wdt

(5)

式(5)中:w为制动盘角速度,rad/s;t为滑移时间,s。

将式(4)、式(5)代入式(3)可得

(6)

在实际制动过程中,磨损因素参数都是随着制动时间发生变化的。对于磨损系数K,其与制动速度和制动压力等众多因素有关,假设其为常数。H的大小主要由摩擦面温度影响,摩擦面温度随制动时间的增大而发生变化,考虑制动热对磨损过程的影响,对表面硬度值进行修正,使其随制动时间的增大而发生动态变化。σ则与制动过程中接触面的状态有关。而制动角速度w则逐渐减小,直至降为0。考虑制动过程各参数实际变化情况,对Archard磨损理论模型进行修正得

(7)

2 有限元模型

2.1 模型的建立及材料参数的设定

2.1.1 模型的建立

不同铁路制动系统,闸片上摩擦块的排列会有所不同。CRH380型列车的闸片上离制动盘中心较远的摩擦块比靠近制动盘中心的摩擦块数量多,而CRH2型列车的闸片上离制动盘中心较远的摩擦块的数量则比靠近制动盘中心的摩擦块少[10]。基于此现象,为反映摩擦块不同排列方式对制动盘磨损的影响,设计离制动盘中心较远的摩擦块比靠近制动盘中心的摩擦块数量多、离制动盘中心较远的摩擦块与靠近制动盘中心的摩擦块数量相同、离制动盘中心较远的摩擦块比靠近制动盘中心的摩擦块数量少3种不同的摩擦块排列方式。

将制动盘的摩擦区域分为内圈、中圈和外圈[10],如图2所示。

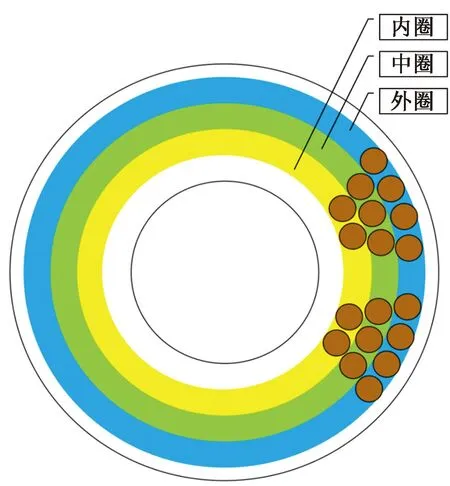
图2 摩擦块与制动盘接触位置示意图Fig.2 Schematic diagram of the contact position between the friction block and the brake disc

将3种排列方式分别记为L1、L2和L3,如图3所示。其中,L1排列(内圈:4块;中圈:6块;外圈:8块),L2排列(内圈:6块;中圈:6块;外圈:6块)和L3排列(内圈:8块;中圈:6块;外圈:4块)摩擦块摩擦面积相同,排列方式不同。

图3 摩擦块,3种排列方式示意图Fig.3 Schematic diagram of three types of friction block arrangement

由于圆形摩擦块的摩擦力较小[15],因此将摩擦块简化为圆形。每种排列所采用的摩擦块数量为18,摩擦块周向间隙相等。制动盘与摩擦块的结构参数如表1所示。

表1 制动盘与摩擦块几何参数Table 1 Geometric parameters of brake disc and friction block

为了简化处理,大多数采用单侧闸片建模。为保证仿真结果的真实性,建立符合实际的两侧闸片制动模型。由于主要目的是研究同等条件下摩擦块排列方式对制动盘磨损的影响,而且磨损主要发生在制动盘的两侧表面,所以暂不考虑其内部散热筋的结构。简化制动盘与两侧闸片模型,最终装配体的离散化模型如图4所示。为便于仿真结果分析,将制动盘左侧摩擦面记为F1,右侧摩擦面记为F2。

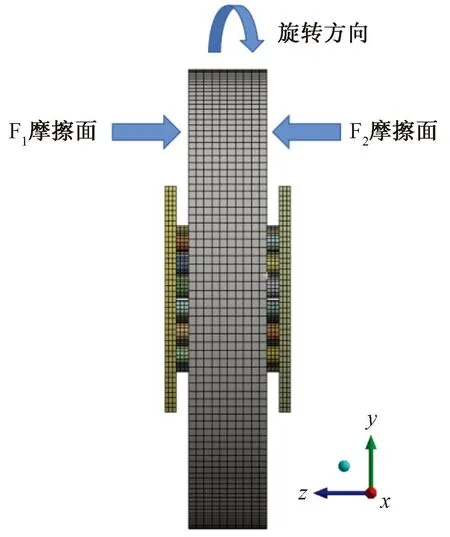
图4 离散化模型Fig.4 Discretisation model

制动盘类型为轴装制动盘,在网格划分中,采用体网格划分(body sizing)来保证网格划分质量[19],各部件均采用精度较高的六面体网格进行划分。制动盘划分后的节点数量为 64 029 个,单元数为 12 521 个,网格单元类型为solid226。由于磨损是表面材料去除的过程,而且在仿真中摩擦接触为边界条件高度非线性的问题,因此为保证接触生效,在网格划分中将摩擦块与制动盘接触面的网格划分尺寸控制在1∶3以内,同时保证划分的网格中不存在畸变单元[20]。

2.1.2 材料参数

制动盘材料为铸钢,摩擦块材料为铜基粉末冶金。为保证仿真结果更加具有真实性,考虑制动材料的力学性能参数和热物理特性参数随摩擦面温度的变化而发生相应的变化。制动盘材料热物理特性参数随温度的变化情况如图5和图6所示,设置仿真初始环境温度为20 ℃。

图5 导热系数及比热容变化曲线Fig.5 Variation curve of thermal conductivity and specific heat capacity

图6 热膨胀系数与温度的关系Fig.6 Relation between the coefficient of thermal expansion and temperature

2.2 边界条件

释放制动盘绕轴旋转的自由度,施加绕轴旋转的转速,并对制动盘其余自由度进行约束。列车初始制动速度为250 km/h,车轮直径为890 mm,对两侧闸片表面施加大小相等、方向相反的法向均布恒定载荷[21]12 000 N。将摩擦块固定在闸片钢背上,并约束钢背的切向自由度,释放其法向自由度。

目前,盘式制动方式下的磨损系数还未有详细的试验数据,在探究制动材料的磨损系数时,选择试验磨损系数[14]。磨损系数K选用Rabinowicz试验[22]中不相似的金属发生磨损时的磨损系数3.3×10-6,摩擦块表面硬度值随温度变化的情况[23]如图7所示。设置制动盘与摩擦块接触面间的摩擦因数为0.4,接触算法选用罚函数,每次迭代自动更新法向刚度。

图7 摩擦块表面硬度与温度关系Fig.7 Relationship between surface hardness and temperature of friction blocks

3 仿真结果与分析

为便于结果分析,将制动盘最大磨损深度记为hmax,最大接触应力记为σmax。

3.1 摩擦块排列方式对最大磨损深度的影响

图8为在L1、L2和L3排列方式下,列车通过42号道岔紧急制动时制动盘F1和F2摩擦面磨损深度最大值的变化情况。中国铁路规定高速列车在通过42号道岔时侧向容许通过速度为160 km/h[24]。从图8(a)可以看出,当制动速度降为160 km/h时,制动盘F1摩擦面hmax最大的是L2排列方式,最大磨损深度值为1.783×10-2mm,L1排列方式制动盘F1摩擦面的hmax最小,最大磨损深度为1.718×10-2mm。从图8(b)可以看出,对于制动盘F2摩擦面来说,hmax最大的也是L2排列方式,最小的是L1排列方式,最大磨损深度分别为1.781×10-2mm和1.711×10-2mm。

不论是制动盘F1摩擦面还是F2摩擦面,3种排列方式在制动过程中最大磨损深度曲线的变化趋势大致相同。在制动初期,L1、L2和L3排列方式的最大磨损深度曲线的斜率变化相近,但当制动速度降为210 km/h开始,3种排列曲线的斜率差异明显。

对比图8(a)和图8(b)可知,同种排列对应F1和F2两摩擦面在相同制动速度下的最大磨损深度数值略有差异,差值不超过1×10-4mm,两摩擦面最大磨损深度曲线变化趋势相同。通过计算制动速度降为160 km/h时F1和F2摩擦面最大磨损深度总和可知,总磨损深度值最大的是L2排列方式,总磨损值为3.565×10-2mm。而总磨损深度值最小的则为L1排列方式,总磨损深度为3.428×10-2mm。综上所述,无论是单侧摩擦面最大磨损深度值还是两侧总磨损深度值,L1排列方式都是最小的,L2排列方式都是最大的。因此选取的3种摩擦块排列方式中,L1为最佳排列方式。

3.2 摩擦块排列方式对最大接触应力的影响

图9为在L1、L2和L3排列方式下,列车通过42号道岔时制动盘F1和F2摩擦面接触应力最大值的变化情况。可以看出,L2排列方式在制动过程中不仅σmax最大且应力波动范围较大,制动不平稳。相反,L1排列方式最大接触应力波动相对平稳且σmax较低,其制动平稳。

图9 F1、F2摩擦面3种排列最大接触应力Fig.9 Maximum contact stress for three arrangements of F1, F2 friction surface

接触应力的大小能够作为评价耐磨性能的指标,接触应力越小,表明其耐磨性能越好[25]。为能够很好反映接触面应力大小对摩擦面磨损深度的影响,提出“应力磨损因子”的概念,实质为制动速度-应力曲线的面积。

应力磨损因子u的表达式为

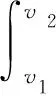
(8)

式(8)中:σ(v)为应力随制动速度v变化值即接触应力变化值,MPa;v1为制动减速度,km/h;v2为制动初速度。

应力磨损因子的表达式为

(9)

应力磨损因子u越小,表示制动盘摩擦面最终的hmax越小。此处分析的是最大接触应力,因此其对应的应力磨损因子即为最大接触应力磨损因子。对于F1摩擦面来说,计算可得L1、L2和L3排列方式的最大接触应力磨损因子u11、u12、u13分别为15.54、29.34、20.96。对于F2摩擦面来说,L1、L2和L3排列方式的最大接触应力磨损因子u21、u22、u23分别为32.53、37.28、34.12。综上可知,不论是F1摩擦面还是F2摩擦面,大接触应力磨损因子最小的都是L1排列方式,这与上述对最大磨损深度的分析中所得出L1排列方式hmax最小的结论一致,进一步验证了L1为最佳排列方式结论的可靠性。

3.3 摩擦块排列方式对磨损形貌的影响

取制动盘F1和F2摩擦面沿径向方向不同摩擦半径处10个节点,如图10所示。当制动速度降为160 km/h时,3种摩擦块排列方式下F1和F2摩擦面上10个节点的磨损深度如图11所示。

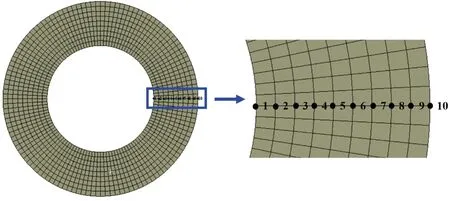
图10 制动盘摩擦面径向10个节点位置图Fig.10 Brake disc friction surface radial 10 nodes location map

图11 F1、F2摩擦面3种排列不同节点磨损深度Fig.11 Depth of wear at different nodes for three arrangements of F1,F2 friction surface

由图11可以看出,对于F1摩擦面来说,磨损易发生在远离制动盘中心处,而对于F2摩擦面来说,磨损易发生在靠近制动盘中心处。L1排列方式F1和F2摩擦面不同摩擦半径处磨损深度曲线相近,即两摩擦面最终的磨损形貌大致相同,而L2和L3排列方式两摩擦面的曲线变化不同,因此最终磨损形貌也略有差异。

图11中的最低点对应制动速度降为160 km/h时制动盘摩擦面所取节点的最大磨损深度,最低点越小,hmax越大。可以看出曲线最低点最小的是L2排列方式、最大的是L1排列方式,这与上述对最大磨损深度分析中所得出L2排列方式hmax最大,L1排列方式hmax最小的结论一致。

观察图11中曲线的变化趋势,可发现L3排列方式两摩擦面偏磨现象相对严重,且L2排列方式磨损曲线近似“W”形,即波浪形异常磨耗,L1排列方式相对来说摩擦面磨损较为均匀。

综上所述,从磨损角度分析,列车通过42号道岔减速制动时,摩擦块采用L1排列方式时对制动盘磨损的伤害最低,即闸片上离制动盘中心较远的摩擦块比靠近制动盘中心的摩擦块多的排列方式为最佳排列方式。

4 结论

基于Archard磨损模型进行修正,利用ANSYS有限元仿真软件,建立制动盘-闸片三维瞬态模型,分析列车在通过42号道岔紧急制动时,采用不同摩擦块的排列方式下制动盘最大磨损深度值。提出“应力磨损因子”参数,对3种不同摩擦块排列方式对制动盘最大磨损深度、最大接触应力、磨损形貌的影响进行仿真分析。得出如下结论。

(1)在摩擦副总接触面积相同的情况下,摩擦块的排列方式会影响制动盘表面的磨损深度和接触应力。合适的闸片结构可以使摩擦能量分布均匀,从而降低制动盘的最大磨损深度与接触应力。摩擦块采用L1排列方式(离制动盘中心较远处摩擦块比靠近制动盘中心的摩擦块的数量多)时,制动盘的最大磨损深度值相对较小。

(2)摩擦块采用L1排列方式时,制动盘摩擦面的最大接触应力值较低且曲线波动较小,制动相对平稳。相反,采用L2排列方式时,制动过程中不仅最大接触应力值较高且应力波动范围较大,制动不平稳。应力磨损因子u越小,表示制动盘摩擦面最大磨损深度值越小。L1排列方式对应的最大接触应力磨损因子最小,进一步验证了L1为最佳排列方式结论的可靠性。

(3)摩擦块采用L3排列方式时,制动盘两摩擦面偏磨现象较为严重,且L2排列方式磨损曲线近似“W”形(波浪形异常磨耗)。而L1排列方式相对来说摩擦面磨损较为均匀,磨损形貌相对平整。