跷板式面板开关触点接触压力一致性参数优化研究*
□ 竺振韬 □ 常秋香 □ 王贤成 □ 余林茂
1.宁波大学 机械工程与力学学院 浙江宁波 315211
2.宁波大学科学技术学院 浙江慈溪 315300
3.宁波公牛电器有限公司 浙江慈溪 315300
1 研究背景
面板开关为机械式结构,操作简便,外观精美,是日常生活中普遍使用的电路控制设备,在低压电器行业中具有较高的市场占有率。国内面板开关研究相较于继电器、断路器等低压电器,设计理论不完善,产品设计大多采用仿制和经验模式。国内企业在批量生产过程中,产品寿命的分散性大,影响人们的日常使用安全[1]。合理的参数组合设计可以保证产品性能要求,公差会影响性能波动范围,设计最佳参数组合并提高公差精度,产品的一致性必然会得到提高。对于低价格且大批量生产的产品而言,改善关键零件的公差,则生产中成本较高。
在现有的研究中,Del Casale等[2]采用参数设计和容差设计方法,确定闭环控制器的最佳参数组合。陈昊等[3]基于Stoner-Wohlfarth模型和Preisach模型,获得非线性永磁体局部磁滞曲线,结合径向基函数提高质量一致性。周月阁等[4]建立基于退化失效时间准则的优化模型,降低功率变换器性能退化敏感性。刘晓明等[5]建立考虑公差不确定性的斥力操动机构保持单元多目标优化设计模型,基于非支配排序粒子群算法的多变量多目标优化方法,获得参数设计公差。目前的研究主要为设计最佳性能,并通过容差设计保证一致性。上述研究通过重新设计容差提高一致性。综合考量下,提高容差势必使成本增加,因此更倾向于采用产品现行公差进行参数优化设计,提高优化目标的一致性。
国内企业对面板开关一致性影响显著的关键设计参数组合无法确定,对此,根据性能一致性和大批量生产中的成本控制要求进行研究[6]。低压电器电寿命与电性能相关,电性能主要包括触点接触电阻[7]、熔焊电流[8]、温升[9]等。触点接触压力与电路通断性能直接相关,是电性能的重要影响参数,受结构设计参数影响较大[10-12]。笔者以某型号跷板式面板开关为研究对象,提高触点接触压力一致性。分析面板开关工作原理,确定影响参数。通过有限元仿真,计算触点接触压力。根据企业现行设计公差,设计正交试验,获取影响因素贡献率。采用Kriging模型建立输入参数与触点接触压力的近似模型,结合非线性二次规划算法确定输出特性在设计公差下的最小波动值,进而确定参数组合。
2 跷板式面板开关工作原理
跷板式面板开关的主要部件包括按钮、过渡件、压板、弹簧、弹子、跷板、动静触点、支撑片、连接片和端子等,结构如图1所示。

图1 跷板式面板开关结构
面板开关根据功能,主要可分为辅助机构、传动机构、执行机构。辅助机构满足用户审美、固定安装、内部机构保护作用。传动机构由按钮、过渡件、压板、弹簧、弹子组成,用于力传递,将外部驱动力改变为合适的执行机构驱动力。执行机构由动静触点、跷板、支撑片、连接片和端子组成,用于实现电路通断。
触点接触过程可分为动态接触过程和静态接触过程。在弹簧系统推动下,弹性势能转换为动触点的动能。动静触点接触,大部分动能转换为触点表面材料的弹性变形和塑性变形。在动态接触过程中,动能和弹性势能来回转换,转换中伴随能量损耗,最终从动态接触转变为静态接触。
由弹性力学接触理论和动能守恒定理,触点碰撞接触压力表示为[13-14]:
F=kδ3/2
(1)
(2)
(3)
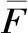
触点稳定接触由弹簧变形保证,根据力矩计算式,弹簧弹力和触点接触压力的关系式为:
F=D2/D1×Fecosθ
(4)
式中:Fe为弹簧弹力;D1为触点接触压力力臂;D2为弹力力臂;θ为弹力偏移角度。
通过上述分析,触点接触压力与触点间距、跷板转动角度、弹簧压缩距离、弹子作用位置等因素有关。根据零件设计图,将静触点高度、支撑片高度、跷板间距作为输入参数。
3 执行机构仿真模型
面板开关主要由注塑件和金属件组成,注塑件优化开模成本高,因此将金属件作为优化部件。执行机构为金属件,将其作为优化部件。触点接触压力测量需要破坏面板开关外壳,对此,采用仿真分析计算。基于零件图纸和产品实测数据,获取零件尺寸和空间位置,通过SolidWorks软件建立执行机构三维模型,如图2所示。

图2 执行机构三维模型
将执行机构三维模型导入ANSYS Workbench软件,利用瞬态结构分析模块进行动力学仿真。对模型添加材料,根据接触面连接方式设置绑定接触、摩擦接触,对过渡件添加转动副,对弹子和过渡件添加平移副和弹簧连接,对弹簧设置1.2 N/mm刚度、12 mm自由长度,加载方式选择过渡件旋转角度代替外部驱动,对其它零件添加固定、位移约束,然后进行计算求解触点接触压力。执行机构建模流程如图3所示。
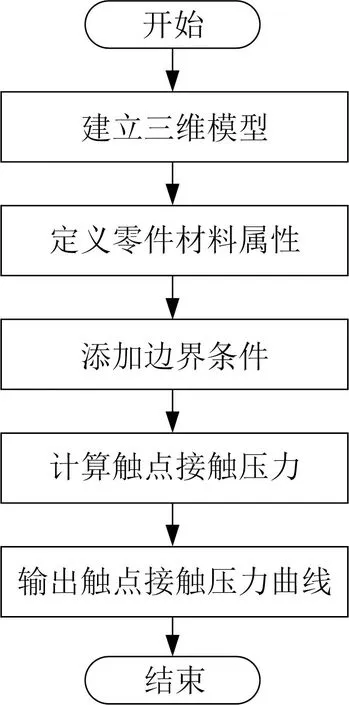
图3 执行机构建模流程
根据仿真结果,不同尺寸参数组合下触点接触压力波动较大,触点接触压力经历陡增、跳动、增长、稳定四个阶段。触点跳动过程弹簧仍在释放弹性势能,起到抑制作用,触点跳动幅度较小。动触点初速度越大,静态接触压力越大。触点接触压力曲线如图4所示,仿真和实测误差约为5%。
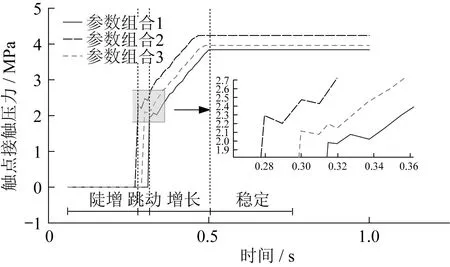
图4 触点接触压力曲线
4 试验设计
试验设计可以最大限度获得有效信息,识别每个输入变量对全局目标响应的影响[15-16]。影响输出特性的因素很多,考虑成本和实际情况,结合模型结构和动力学分析,选取静触点高度、支撑片高度、跷板间距作为输入变量。
采用正交试验设计,将三个输入变量记作因素A、因素B、因素C,将现有设计值作为中心值,根据零件强度要求、工艺要求、生产经验确定参数模糊区间,控制优化加工成本,以现行加工精度为约束节点。
正交试验中,为确定最佳参数组合,以粗加工公差作为边界值,对公差上下限各增加一个水平,试验因素水平表见表1,第一水平为参数下边界,第二水平为参数中心值减参数偏差,第三水平为参数中心值,第四水平为参数中心值加参数偏差,第五水平为参数上边界。

表1 试验因素水平表
通过正交试验,分析各因素对触点接触压力的影响,不考虑各因素之间的相互作用。采用L25(53) 正交表,需进行25次试验,获得动静触点间接触压力输出特性值。正交试验结果见表2,μ1~μ5表示对应水平下的输出特性均值,Delta表示各因素五水平试验均值极差,反映各因素对输出特性的影响程度。对于触点接触压力,影响因素从主到次排序为支撑片高度、静触点高度、跷板间距。均值主效应图如图5所示。

表2 正交试验结果
图5 均值主效应图
5 Kriging模型
正交试验通过特殊试验组数确保试验的均衡性和有效性,未包含所有水平组合情况,需建立输入变量与输出特性关系进行预测。Kriging模型是一种用于插值和预测的统计模型,根据采样点数据建立输入与输出参数之间的函数关系,对输入量进行快速计算,避免烦琐的仿真计算求解[17]。Kriging模型相较于响应面模型等对高维非线性问题拟合效果较好,相较于人工神经网络所需样本数量少。Kriging模型建模是对目标函数在求解区域内寻求最优无偏估计的过程,建立静触点高度、支撑片高度、跷板间距与触点接触压力的关系函数。Kriging模型表达式为[18]:
(5)
(6)
rT(γ)=[R(γ,γ1),R(γ,γ2),…,R(γ,γm)]T
(7)
(8)
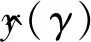
模型拟合度误差分析为0.95,预测效果较好。拟合度误差分析表达式为:
R2=SSR/SST=1-SSE/SST
(9)
(10)
(11)
(12)

6 优化模型
对跷板式面板开关的触点接触压力一致性进行优化,在不改变结构形状和参数公差精度的前提下,对参数组合进行优化,要求触点接触压力波动最小。触点接触压力最小值为1.1 N,限制参数边界和参数公差值。目标函数为min(Δyi),约束为:
ymin≥1.1 N
10.6 mm≤A≤11.3 mm
10.7 mm≤B≤11.3 mm
2.85 mm≤C≤3.15 mm
ΔA=0.3 mm
ΔB=0.2 mm
ΔC=0.1 mm
Δyi为各参数组合下的波动值,ymin为输出特性最小值,A为因素A,B为因素B,C为因素C,ΔA、ΔB、ΔC为各因素公差。
7 优化流程
采用非线性二次规划算法,求解获取输出特性波动值的最大值和最小值。非线性二次规划算法利用二次规划,将原始的非线性规划问题转换为一系列二次规划子问题,并通过求解这些二次规划子问题来逼近最优解[19-20]。对因素A、因素B、因素C以各自公差进行分组,并进行排列组合,确定参数区间,经非线性二次规划算法获得输出特性最大最小值,计算确定最小输出特性波动范围和最佳参数组合。参数优化流程如图6所示。为减少计算次数,进行分级优化,根据参数优先级确认最佳组别,计算次数从nk1减少至k1n,n为参数组别数,k1为参数数量。
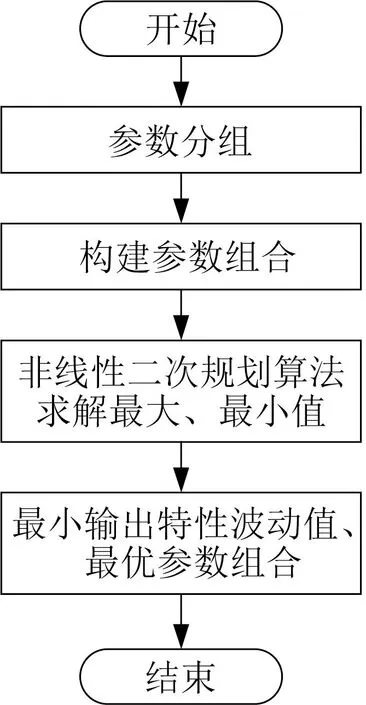
图6 参数优化流程
8 优化结果
通过非线性二次规划算法,求解获得不同参数下的触点接触压力值波动范围。根据参数影响优先级,将因素B作为首要约束条件,因素B影响下的触点接触压力在B2至B5范围内波动相近,在B1范围内波动最小。结合最小触点接触压力设计需求,选取B4(10.9~11.1 mm)作为支撑片高度尺寸区间。在因素B约束条件下,计算因素A约束下的触点接触压力变化,从A1至A5触点接触压力波动呈减小趋势,选取A5(11~11.3 mm)作为静触点高度尺寸区间。因素A、因素B确定后,C1范围内触点接触压力波动最小,C4范围内触点接触压力波动最大,选取C1(2.85~2.95 mm)作为跷板间距尺寸区间。各因素组合下触点接触压力波动见表3。A1至A5的中心值分别为10.7 mm、10.8 mm、10.9 mm、11.0 mm、11.1 mm,B1至B5的中心值分别为10.8 mm、10.9 mm、11.0 mm、11.1 mm、11.2 mm,C1至C5的中心值分别为2.90 mm、2.95 mm、3.00 mm、3.05 mm、3.10 mm。
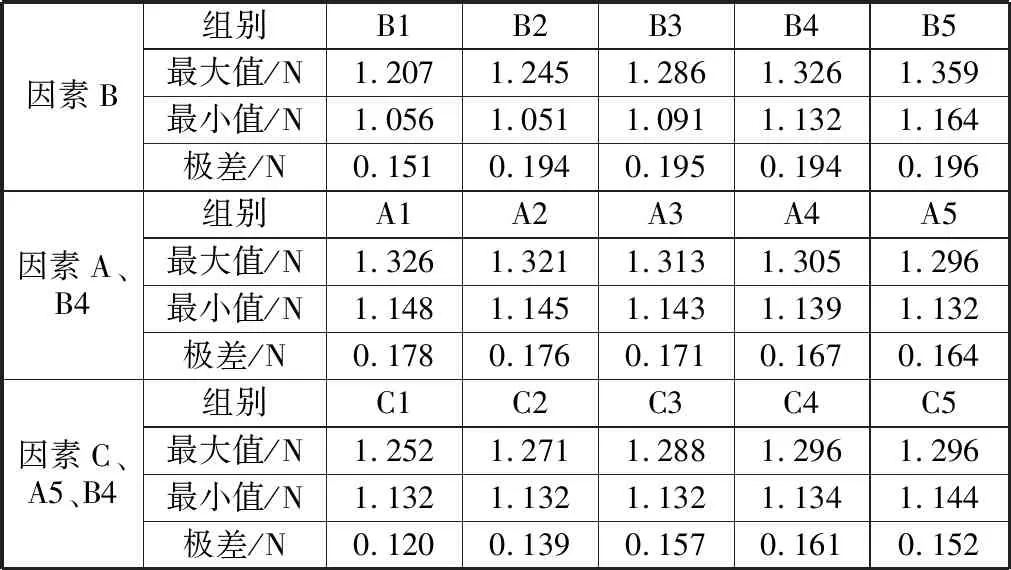
表3 各因素组合下触点接触压力波动
因素B约束下输出特性波动如图7所示,因素A和B4约束下输出特性波动如图8所示, 因素C和A5、B4约束下输出特性波动如图9所示,输出特性波动重叠如图10所示。

图7 因素B约束下输出特性波动

图8 因素A和B4约束下输出特性波动

图9 因素C和A5、B4约束下输出特性波动
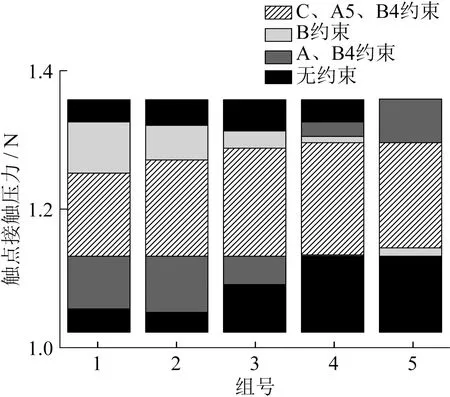
图10 输出特性波动重叠
选取A5、B4、C1作为触点接触压力优化组合,优化前后对比见表4。模型计算触点接触压力波动范围减小14.9%。通过试制样品实际测量,触点接触压力从1.11~1.25 N变为1.12~1.19 N,波动减小50%。实际测量装置如图11所示。
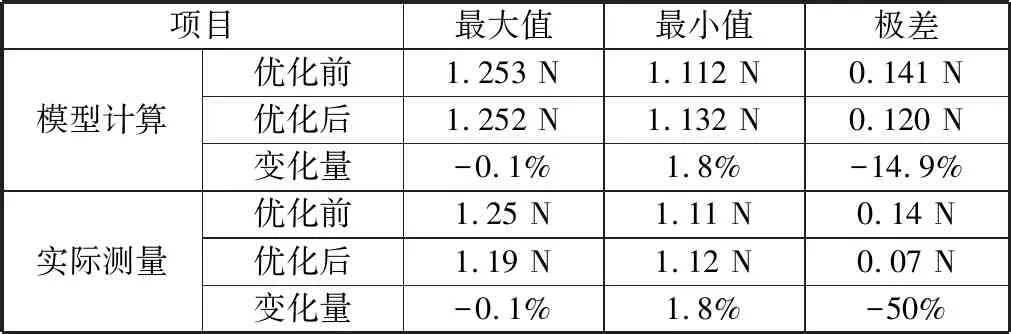
表4 触点接触压力优化前后对比

图11 实际测量装置
9 结束语
笔者选取跷板式面板开关的执行机构作为研究对象,对动静触点间的接触压力进行有限元分析。针对触点接触压力一致性问题,采用正交试验、Kriging模型、非线性二次规划算法等进行分析优化。
在跷板式面板开关执行机构中,静触点高度、支撑片高度、跷板间距对触点接触压力影响显著,贡献率从高到低为支撑片高度、静触点高度、跷板间距。
在企业现行设计公差条件下,最佳性能参数组合并非性能一致性最佳参数组合,触点接触压力一致性提高50%。
笔者计算模型将参数转换为线性关系,实际参数为离散点,计算模型与实际数值存在偏差,但能反映数值变化趋势,为产品设计提供参考。如果最佳输出特性的参数组合和一致性的参数组合相同,那么为进一步提高输出特性一致性,需提高参数公差或对结构进行优化。

